JUMP TO TOPIC
Cube|Definition & Meaning
Definition of Cube
A cube is a three-dimensional geometrical solid shape that has six sides and each side is square. Each square side has the same length which means that all the sides are equal. This geometric shape has twelve edges and eight vertices. The corner where the three edges of a cube meet are the vertex of that cube.
Cubic is usually referred to as objects that have a cube shape. It is in the shape of a solid block that has the length, width, and height, all in the same or equal length. There are some other names for cube shapes like square parallelepipeds, equilateral cuboids, or right rhombohedrons.
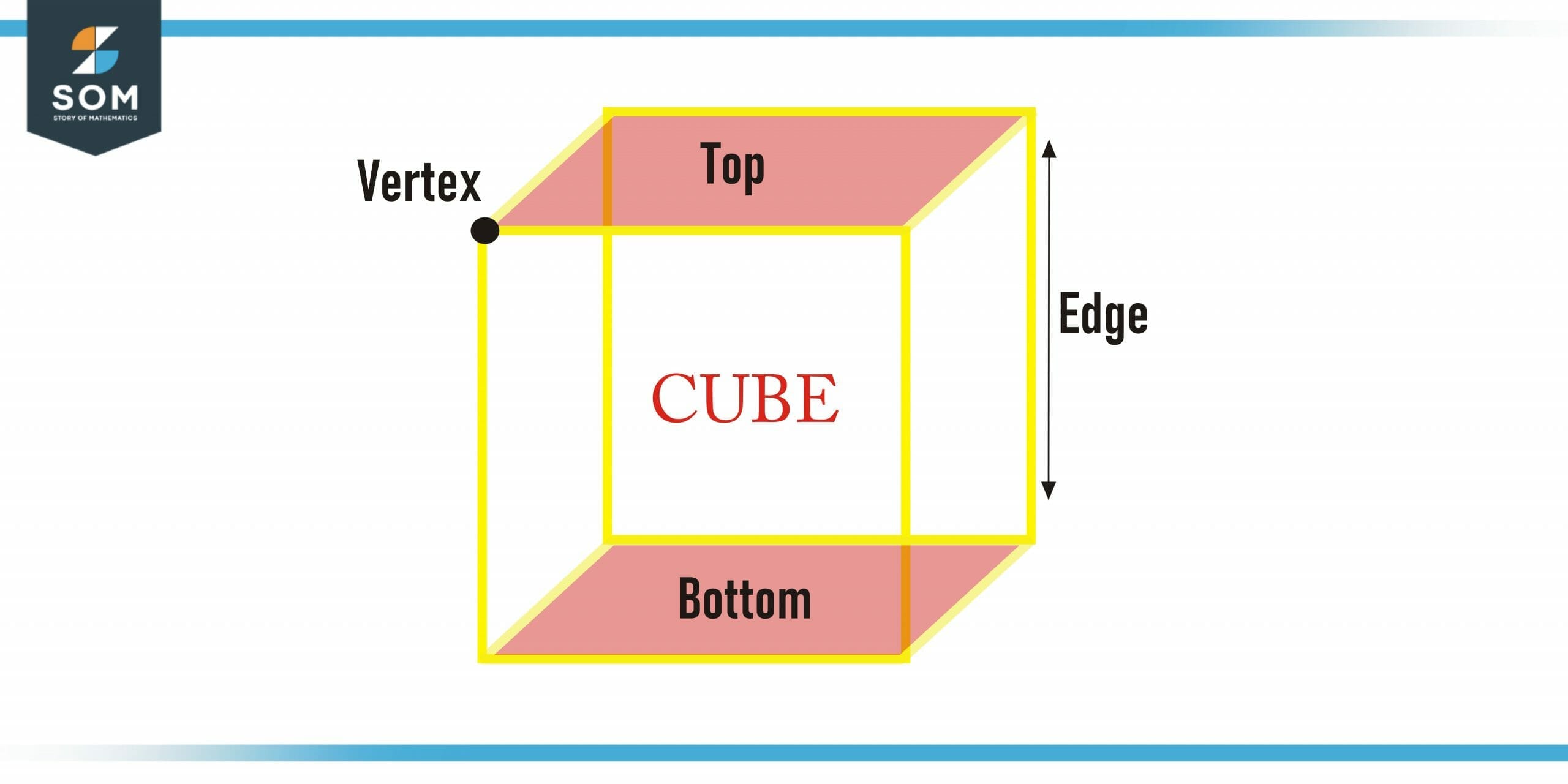
Figure 1 – Labeled Diagram of a cube
Labeled Diagram of a Cube Shape
A cube shape has three basic parts i.e Face, edge, and vertex of the cube. In this figure we have marked length with L, H for height and B stands for the breadth of the cube. Usually, the same symbolic representation is used for a cube shape.
Now, if we focus on the length, width, and breadth, we can see that all these three lengths, which are actually the edges of the cube, meet at one corner of the cube, this corner is the vertex of the cube and every cube has 8 vertices. Each face of the cube has four vertices.
Properties of Cube
- 3D shape
- It has Twelve Edges, six faces, and eighth vertices
- All faces are square shaped
- All sides have the same dimensions i.e. length, breadth, and height
- The right angle is formed at the planes
- All the faces are in touch with other faces
- Opposite edges are parallel to each other.
- Every vertex meets the three faces and three edges of the cube.
- The opposite faces are parallel in a cube.
Lateral Surface Area of Cube
Suppose you are standing in a block that is cube–shaped. If you head straight and rotate yourself 360 degrees. During this complete rotation, the area you see on the side of the cube-shaped block is the lateral surface area of that cube.
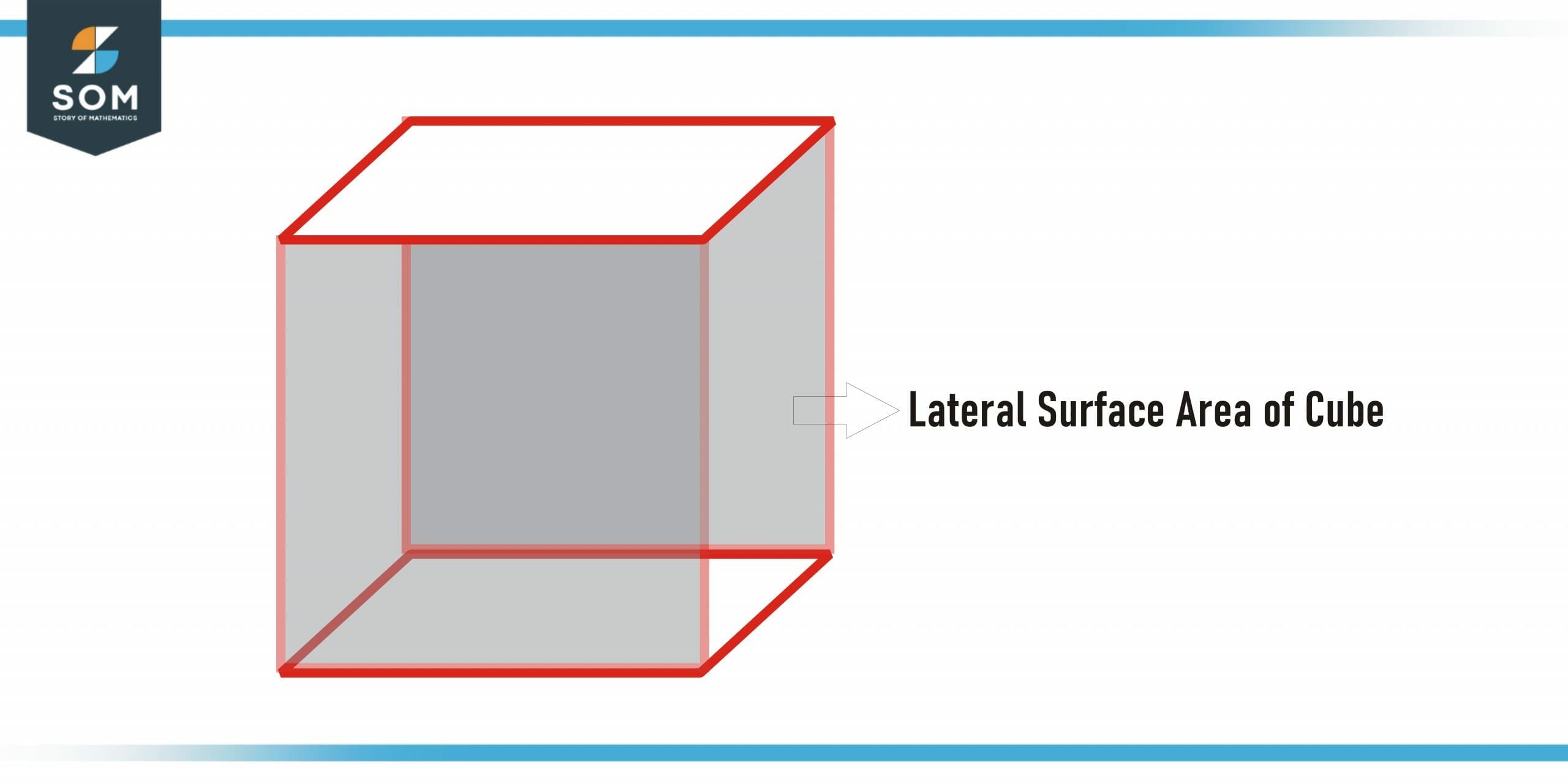
Figure 2 – The Lateral surface area of a cube
Mathematically, the sum of areas of four sides or faces of a cube that excludes the top side and the lower side of the cube is known as the lateral surface area of the cube.
Lateral surface area of the cube = sum of areas of four sides = 4x$^2$
Here, x is the length of the edge.
Surface Area of Cube
As we know, all geometrical shapes have some geometry or regularization, allowing us to perform some simple calculations on them. So, the same is the case for cubes. It also has some surface area that can be easily calculated.
In general, the area or region utilized or covered by the plane surface is known as Surface Area. In this case, our shape or object is three-dimensional, which means that the area covered by it will also be in a three-dimensional plane.
There are six sides or faces of a cube. The total surface area can be calculated if we have the surface area of the sides, these sides actually make the surface of a cube. Mathematically, the sum of the lateral surface area and top and bottom sides gives the total surface area of the cube.
Let’s suppose that the length of the edge of the cube is x:
Area of one side or face = area of square = x$^2$
As we know, the total area will be the sum of the lateral surface area and the top and bottom sides. So:
Lateral surface area = 4x$^2$
Area of top and bottom face = 2x$^2$
Finally:
The total surface area of cube = A = lateral surface area + top and bottom surfaces are
= 4x$^2$ + 2x$^2$
= 6x$^2$
Volume of Cube
The volume of a three-dimensional geometric shape is the space contained in it or in other words it can be said that the amount of liquid that this shape can hold inside it. For example, we have a cube-shaped container and we fill it with water, the amount of water it holds is the volume of this cube-shaped object.
Generally, volume is the product of the length, breadth, and height of the object. For cubes, the same mathematics is applied, but here as we already know that for cubes the length, breadth, and height are always equal length so,
L = B = H = x
Then:
x.x.x = x$^3$
Therefore:
Volume of the cube = x$^3$ cubic units.
Difference Between Square and Cube
The basic difference between a square shape and a cube shape is their dimension. A Square is a two-dimensional shape while a cube is a three-dimensional shape. A Square has only length and width while a cube has breadth along with length and height. A cube is formed by a combination of square shapes.
Solved Examples Relate to Cube
The following examples will elaborate on the problem-solving techniques regarding cubes. Both mathematical and practical examples are solved below.
Example 1 – Mathematical Approach
A cube has a side length of 5 cm. Find the surface area and volume of this cube.
Solution
Given that:
Length of one side = x = 5 cm
As we know:
Surface area of cube = 6x$^2$
= 6(5)$^2$
= 6(25)
= 150 cm$^2$
So, the surface area of the given cube is 150 square centimeters. Now, the volume of a cube is given by:
Volume = x$^3$
(5)$^3$ = 125 cm$^3$
Hence, the volume of this cube is 125 cubic centimeters.
Example 2 – Real-life problem
Jon is given a hollow block that has a cubic shape. His teacher puts 729 cubic centimeters of water in it and asks him to calculate the length of the side of that block.
Note: No measuring instrument is available. How will Jon find the solution to this problem?
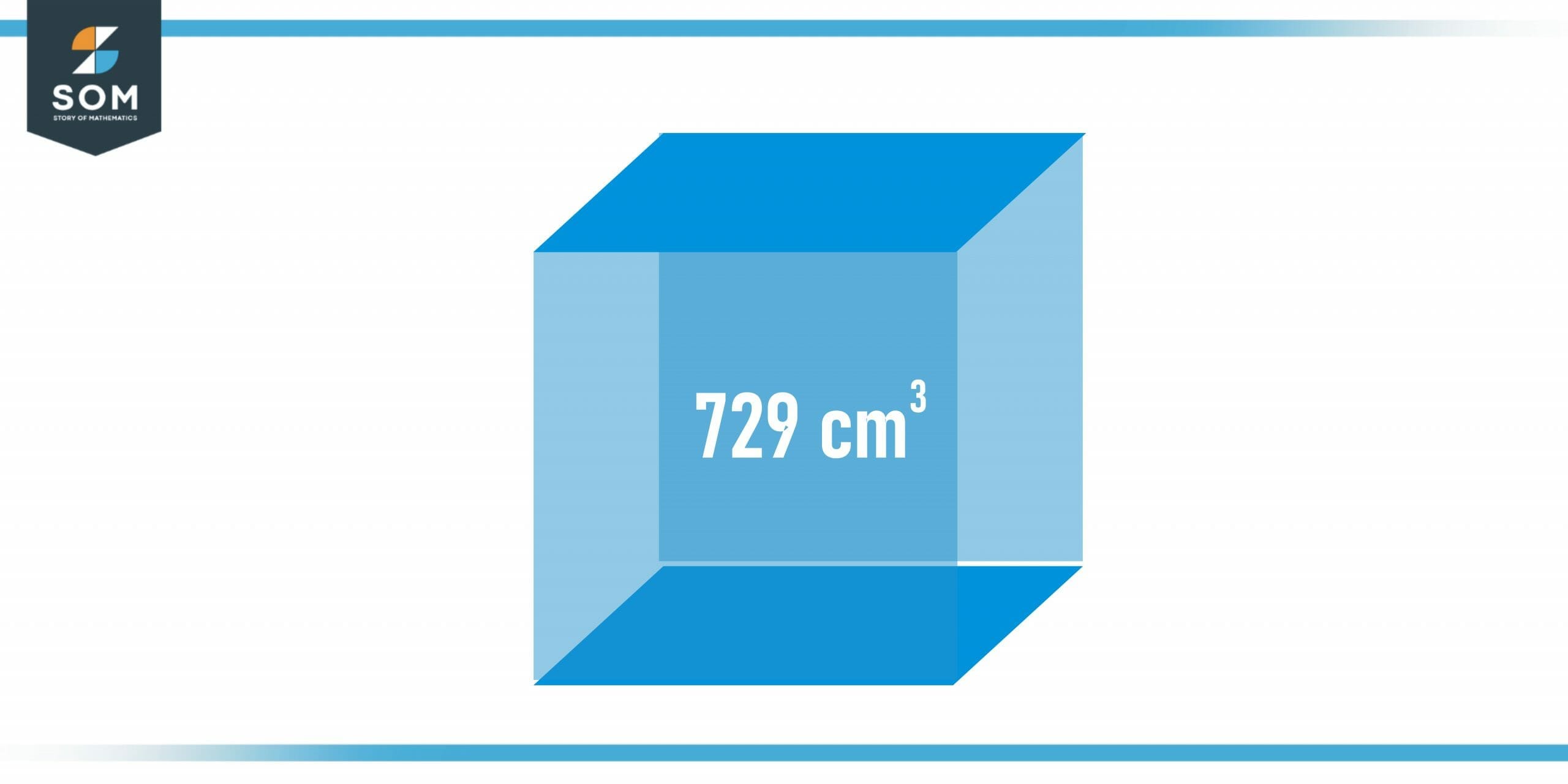
Figure 3 – A cubic box containing 729 cubic centimeters of water
Solution
Volume of cube = v = 729 cm$^3$
v = x$^3$
So, x$^3$ = 729 cm$^3$
Now, take the cube root of LHS and Right Hand Side:
x = 9 cm
Hence, each side of the given block is 9 cm in length.
All images/mathematical drawings were created with GeoGebra.
