Distance between polar coordinates – Derivation, Process, and Examples

We can find the distance between polar coordinates by revisiting the distance formula. Knowing this technique will come in handy when we want to find the distance between two or more polar coordinates, and we don’t want to convert them into their rectangular forms.

We can find the distance between two polar coordinates using the values of their radii and their arguments.

This article will show how we can derive the polar coordinates’ distance formula and learn how to apply it in different examples and problems. Before we do so, make sure to review your notes on the following:

• Make sure to understand the different components needed for us to apply the distance formula in rectangular coordinates.
• Review your knowledge of polar forms and converting rectangular expressions to their polar forms.
• Refresh your knowledge on the most common trigonometric identities you’ve learned in the past.

Let’s go ahead and dive right into the formula and the process of finding the distance between two or more polar coordinates.

How to find the distance between polar coordinates?               

The best way to understand how we can apply the distance formula for polar coordinates is by deriving the formula from the distance formula for rectangular coordinates.

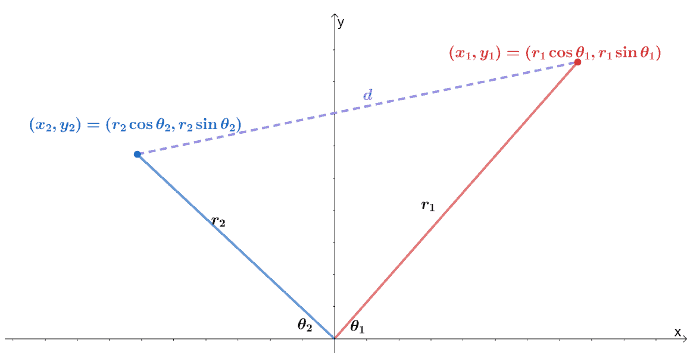
Here’s a visualization of how two polar coordinates be on an $xy$-coordinate system. Recall that the distance between two points, $(x_1, y_1)$ and $(x_2, y_2)$, is equal to $\sqrt{(y_2 – y_1)^2 + (x_2 – x_1)^2}$.

We can express the two points as two polar coordinates, $(r_1 \cos \theta_1, r_1 \sin \theta_1)$ and $(r_2 \cos \theta_1, r_2 \sin \theta_1)$. We can then rewrite the distance formula in terms of the radius and the argument of the polar coordinates.

\begin{aligned}d &= \sqrt{(y_2 – y_1)^2 + (x_2 – x_1)^2}\\d &= \sqrt{(r_2 \sin\theta_2 – r_1 \sin\theta_1)^2 + (r_2 \cos \theta_2 – r_1 \cos \theta_1)^2}\end{aligned}

We can expand the terms inside the square root using the algebraic property, $(a -b)^2 = a^2 -2ab + b^2$, then simplify the terms as shown below.

\begin{aligned}d &= \sqrt{(r_2^{\phantom{x}2} \sin\theta_2 -2 r_1r_2\cos\theta_1\sin\theta_2 + r_1^{\phantom{x}2} \sin^2\theta_1) + (r_2^{\phantom{x}2} \cos\theta_2 -2 r_1r_2\sin\theta_1\cos\theta_2 + r_1^{\phantom{x}2} \cos^2\theta_1)}\\&= \sqrt{ (r_1^{\phantom{x}2}\cos^2\theta_1 + r_1^{\phantom{x}2} \sin^2\theta_1) + (r_2^{\phantom{x}2}\cos^2\theta_2 + r_2^{\phantom{x}2} \sin^2\theta_2) -(2 r_1r_2\cos\theta_1\sin\theta_2  +2 r_1r_2\sin\theta_1\cos\theta_2) }\\&= \sqrt{ r_1^{\phantom{x}2} (\cos^2\theta_1 + \sin^2\theta_1) + r_2^{\phantom{x}2}(\cos^2\theta_2 + \sin^2\theta_2) -2r_1r_2(\cos\theta_1\sin\theta_2  +\sin\theta_1\cos\theta_2) }\end{aligned}

Does pair look familiar to you? That’s because we can rewrite them using the following trigonometric identities:

• $\sin^2 A + \cos^2 A = 1$
• $\cos(A -B) = \cos A \cos B + \sin A \sin B$

\begin{aligned}d &= \sqrt{ r_1^{\phantom{x}2} (1) + r_2^{\phantom{x}2}(1) -2r_1r_2\cos(\theta_1  -\theta_2) }\\&= \sqrt{ r_1^{\phantom{x}2} + r_2^{\phantom{x}2} -2r_1r_2\cos(\theta_1  -\theta_2) } \end{aligned}

Hence, we’ve shown you that we can find the distance between two polar coordinates using the polar coordinates’ distance formula shown below:

\begin{aligned}&\phantom{xxxxx}(r_1, \theta_1)\\ &\phantom{xxxxx}(r_2, \theta_2)\\\\d &= \sqrt{ r_1^{\phantom{x}2} + r_2^{\phantom{x}2} -2r_1r_2\cos(\theta_1  -\theta_2) } \end{aligned}

Applying the distance between polar coordinates formula

The formula shown above tells that there is no need for us to convert the polar coordinates to rectangular coordinates so that we calculate for their distance. Given two points, $(r_1, \theta_1)$ and $(r_2, \theta_2)$, we can apply the following steps:s

• Find the values for $r_1$ and eventually the value of $r_1^{\phantom{x}2}$ .
• We can do the same for $r_2$ and $ r_2^{\phantom{x}2}$.
• Find the difference between their angles, $(theta_1 – \theta_2)$.
• Use these components to find the distance between the two points using the formula, $d = \sqrt{ r_1^{\phantom{x}2} + r_2^{\phantom{x}2} -2r_1r_2\cos(\theta_1  -\theta_2) }$.

Let’s say we have $(-3, 75^{\circ})$ and $(6, 45^{\circ})$, we can the distance between the two points by using the polar coordinate’s distance formula. We can begin by identifying the components and the essential values for the formula:

We can also use our calculator to estimate the exact value of the distance between the two polar coordinates. This means that $d = \sqrt{45 + 18\sqrt{3}} \approx 8.73$ units.

We’ve now shown you how to derive and apply the formula for the polar coordinates’ distance, so it’s time for you to test your knowledge by answering the problems shown below.

Example 1

Determine length of the line-segment joining the polar coordinates $(6, 80^{\circ})$ and $(3, 20^{\circ})$.

Solution

Begin by identifying the important values we need to calculate for the distance between the two polar coordinates.

• $r_1 = 6$, $\theta_1 = 80^{\circ}$
• $r_2 = 3$, $\theta_2 = 20^{\circ}$

\begin{aligned}d &= \sqrt{ r_1^{\phantom{x}2} + r_2^{\phantom{x}2} -2r_1r_2\cos(\theta_1  -\theta_2) }\\&= \sqrt{36 + 9 -2(6)(3)\cos 60^{\circ} }\\&=\sqrt{45 – 36\cos 60^{\circ}}\\ &=\sqrt{45 – 36\cdot \dfrac{1}{2}}\\&=\sqrt{45 – 18}\\&= \sqrt{27}\\&= 3\sqrt{3} \end{aligned}

This means that the distance between the two polar coordinates, $(6, 80^{\circ})$ and $(3, 20^{\circ})$, is equal to $3\sqrt{3}$ or approximately $5.20$ units.

Example 2

Given two polar points, $P_1$ and $P_2$, calculate the distance between the points.

\begin{aligned}P_1 &= \left(4, \dfrac{2\pi}{3}\right)\\P_2 &= \left(8, \dfrac{\pi}{6}\right)\end{aligned}

Solution

We’ll apply the same formula to find the distance between $P_1$ and $P_2$, but this time, we’re working with angles in radians. As before, let’s take note of the important components we’ll need for the distance formula.

• $r_1 = 4$, $\theta_1 = \dfrac{2\pi}{3}$
• $r_2 = 8$, $\theta_2 = \dfrac{\pi}{6}$

\begin{aligned}d &= \sqrt{ r_1^{\phantom{x}2} + r_2^{\phantom{x}2} -2r_1r_2\cos(\theta_1  -\theta_2) }\\&= \sqrt{16 + 64 -2(4)(8)\cos\dfrac{\pi}{2} }\\&=\sqrt{80 – 64\cos \dfrac{\pi}{2}}\\ &=\sqrt{80 – 0}\\&=\sqrt{80}\\&= 4\sqrt{5}\end{aligned}

This means that the distance between $P_1$ and $P_2$ is equal to $4\sqrt{5}$ or approximately $8.94$ units.

Before we move on to the third example, observe how important it is to familiarize ourselves with the special angles in trigonometry. Knowing their trigonometric values will make calculating the distance much faster. Another tip: double-check your calculator’s degree mode ($\text{DEG}$ for $^{\circ}$ and $\text{RAD}$ for radians).

Example 3

The four polar coordinates, $A$, $B$, $C$, and $D$, are plotted on an $xy$-coordinate system as shown below. 

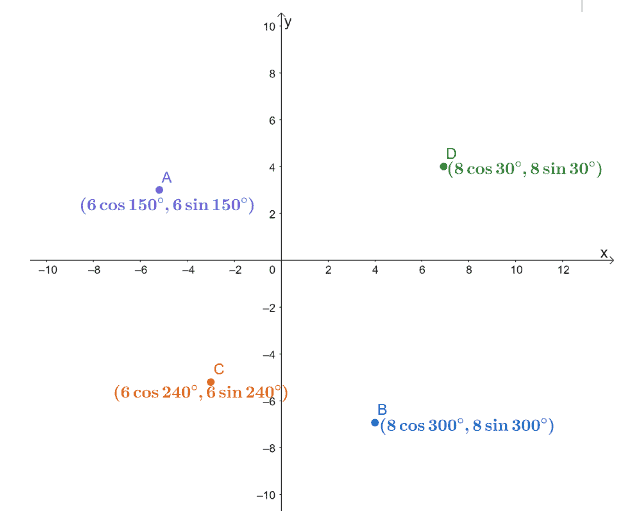
Find the distances of the following pairs of points.
a. Distance between $A$ and $C$.
b. Distance between $B$ and $C$.
c. Distance between $B$ and $D$.
Use the result to find which of the three segments, $\overline{AC}$, $\overline{BC}$, as well as $\overline{BD}$, are the shortest and the longest.

Solution

We can find the distances of all pairs by using the same distance formula for polar coordinates as shown below.

\begin{aligned}d &= \sqrt{ r_1^{\phantom{x}2} + r_2^{\phantom{x}2} -2r_1r_2\cos(\theta_1  -\theta_2) }\end{aligned}

We can start with the first pair of polar coordinates: $A$ and $C$.

• $r_1 = 6$, $\theta_1 = 150^{\circ}$
• $r_2 = 6$, $\theta_2 = 240^{\circ}$

Let’s enter these values into the distance formula and have the following results:

\begin{aligned}d &= \sqrt{ r_1^{\phantom{x}2} + r_2^{\phantom{x}2} -2r_1r_2\cos(\theta_1  -\theta_2) }\\&= \sqrt{36 + 36 -2(6)(6)\cos(240^{\circ}-150^{\circ})}\\&=\sqrt{72 – 72\cos 90^{\circ}}\\ &=\sqrt{72 – 0}\\&=\sqrt{72}\\&= 6\sqrt{2}\end{aligned}

From this, we can see that the distance between $A$ and $B$ is equal to $6\sqrt{2}$ units or approximately, $8.49$ units. We can apply a similar approach to find the distances between b) $B$ and $C$ and c)$B$ and $D$. We can summarize the results in a table as shown below:

We’ve shown you the distances between the two pairs of points. Now, to answer the follow-up question, we can compare the distances of $\overline{AC}$, $\overline{BC}$, and $\overline{BD}$.

\begin{aligned}\overline{AC} &= 8.49\text{ units}\\\overline{BC} &= 7.21\text{ units}\\\overline{BD} &= 11.31\text{ units}\end{aligned}

Comparing the three, we can see that the longest segment will be $\overline{BD}$ and the shortest segment will be $\overline{BC}$.