JUMP TO TOPIC
Factors of 150: Prime Factorization, Methods, Tree, And Examples
The Factors of 150 are the numbers upon which the number 150 is completely divisible. Being completely divisible means that these numbers yield zero as the remainder when they act as the divisors for the number 150.
Figure 1 – All possible Factors of 150
What Are the Factors of 150?
The factors of 150 are the following: 1, 2, 3, 5, 6, 10, 15, 25, 30, 50, 75, and 150. All these numbers give off zero as the remainder when they act as the divisors for the number 150.As the number 150 is an even composite number so it has 12 factors in total. These 12 factors can form 6 factor pairs.How To Calculate the Factors of 150?
You can calculate the factors of 150 through various methods but one of the most reliable methods to do so is the division method. The division method, as the name itself suggests, is based on the operation of division.Prior to moving towards the application of the decision method on the number 150, it is first necessary to determine the range in which these factors lie. This is because the number 150 is a big number and an infinite number of possibilities exist for factors.So to narrow down those possibilities, it is necessary to determine the range. The method for determining the range of the factors is to look for the half of that number. In this case, the number is 150 and it’s half is 75. So this indicates that the range of factors of 150 lies between 1 and 75. Therefore, the division method will be applied to the numbers existing between 1 and 75.The condition for a number to be verified as a factor is that when it undergoes the division method, the number must leave zero as the remainder and a whole number quotient. This quotient rendered through the division also acts as the factor for the original number.As for the factors of 150, we know that the number 1 and the number 150 already qualify as the factors. We also know that the number 150 is an even number so this indicates that the number 2 will also act as its factor. The division is shown below:\[ \frac{150}{2} = 75 \]The division of this quotient 75 with the number 150 is shown below:\[ \frac{150}{75} = 2 \]So the number 75 also qualifies to be a factor of 150. Additional factors of 150 are given below:\[ \frac{150}{1} = 150 \]\[ \frac{150}{3} = 50 \]\[ \frac{150}{5} = 30 \]\[ \frac{150}{6} = 25 \]\[ \frac{150}{10} = 15 \]\[ \frac{150}{15} = 10 \]\[ \frac{150}{25} = 6 \]\[ \frac{150}{30} = 5 \]\[ \frac{150}{50} = 3 \]\[ \frac{150}{150} = 1\]Hence, the total factors of 150 are given below:Factors of 150: 1, 2, 3, 5, 6, 10, 15, 25, 30, 50, 75, and 150 The factors for any number can be both positive and negative. The only difference between the two factors is the sign. The positive factors have a positive (+) sign whereas the negative factors have a negative (-) sign.The list of negative factors of the number 150 is given below:Negative Factors of 150: -1, -2, -3, -5, -6, -10, -15, -25, -30, -50, -75, and -150Factors of 150 by Prime Factorization
The prime factorization method is the method that is used to evaluate the prime factors for a given number. This method is based on the operation of division. In prime factorization, the entire division is carried out by prime numbers only.Like every other division, whole number quotients are also produced in prime factorization as a result of the division. These whole number quotients are passed onto the next step where they become the dividend for a potential prime factor.This process of division with prime numbers is continued till 1 is achieved at the end. The prime factorization of the number 150 is shown below:150 $\div$ 5 = 30
30 $\div$ 5 = 6
6 $\div$ 2 = 3
3 $\div$ 3 = 1
As we get 1 in the last equation, so the prime factorization process terminates here. The divisions in the prime factorization method can be collectively written as follows:Prime Factorization of 150 = 2 x 3 x 5 x 5
OrPrime Factorization of 150 = 2 x 3 x $5^{2}$
This prime factorization is also represented in figure 2 given below: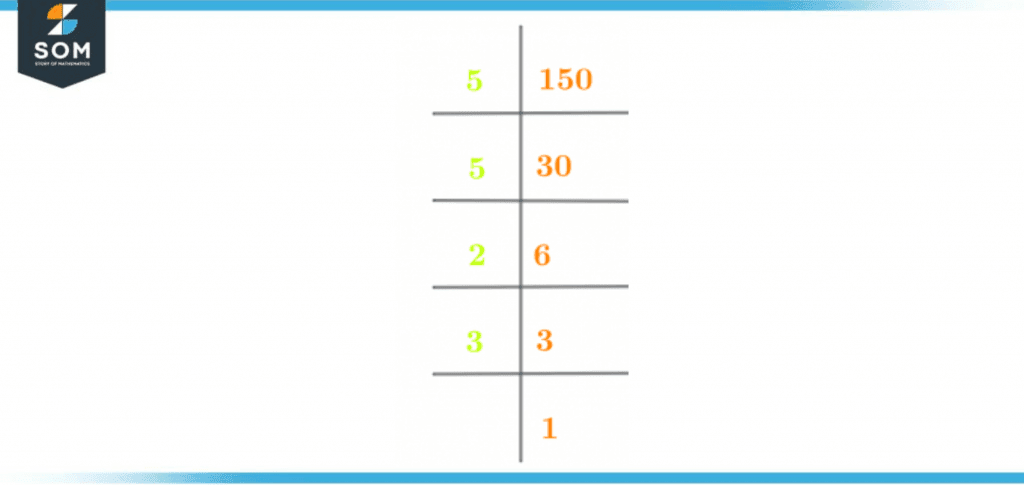
Figure 2 – Prime Factorization of 150
Factor Tree of 150
The factor tree is the technique for pictorially representing the prime factors. It has a tree-like structure with multiple branches holding various numbers. The factor tree only holds prime numbers in its last branches. The factor tree for the number 150 is shown in figure 3 below: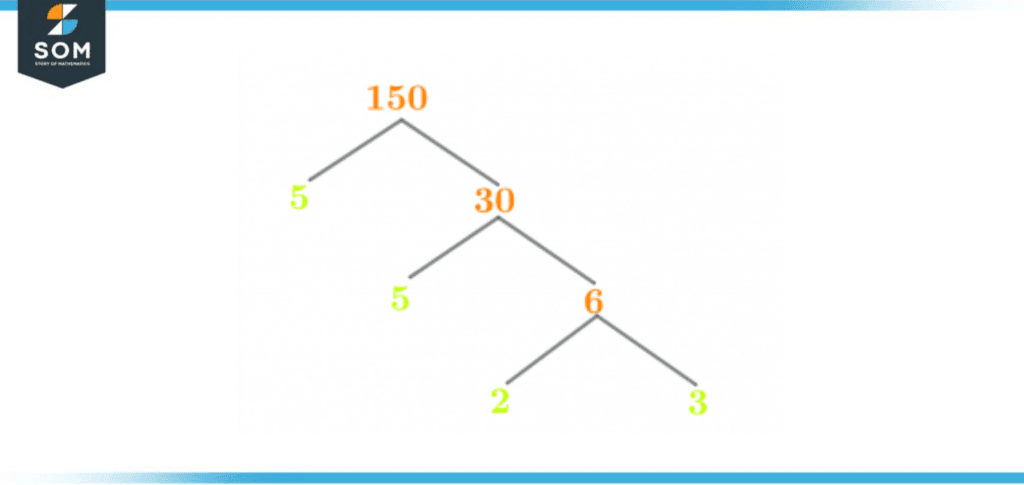
Figure 3 – Factor Tree of 150
Factors of 150 in Pairs
The factors of 150 also have the ability to exist in the form of pairs which are known as the factor pairs. A factor pair consists of two numbers that undergo the process of multiplication. As a result of this multiplication, the original number must be produced as the result.The number 150 has 12 factors in total so these 12 factors can exist in 6 factor pairs. These factor pairs are given below:1 x 150 = 150
2 x 75 = 150
3 x 50 = 150
5 x 30 = 150
6 x 25 = 150
10 x 15 = 150
Factor Pairs of 150 = (1, 150), (2, 75), (3, 50), (5, 30), (6, 25), and (10, 15)The factor pairs of 150 can also be negative factor pairs. The only specification required for negative factor pairs is that both the numbers within the pair must have a negative sign. This is because the multiplication of these negative numbers results in a positive product.The negative factor pairs are given below:-1 x -150 = 150
-2 x -75 = 150
-3 x -50 = 150
-5 x -30 = 150
-6 x -25 = 150
-10 x -15 = 150
Negative Factor Pairs of 150 = (-1, -150), (-2, -75), (-3, -50), (-5, -30), (-6, -25), and (-10, -15)Factors of 150 Solved Examples
To strengthen the understanding of the factors of 150, let’s take a dive into some solved examples involving the factors of 150.Example 1
Determine the sum of the factors of 150 and figure out if this number is a multiple of 2 or 3.Solution
To determine the sum of the factors of 150, let’s first list these factors down. Factors of 150 are given below:Factors of 150 = 1, 2, 3, 5, 6, 10, 15, 25, 30, 50, 75, and 150Now, let’s calculate the sum of these 12 factors. Calculating their sum:Sum of factors of 150 = 1 + 2 + 3 + 5 + 6 + 10 + 15 + 25 + 30 + 50 + 75 + 150
Sum of factors of 150 = 372
As the result obtained, 372, is an even number so this indicates that the number 372 is a multiple of 2 as shown below in the multiplication:2 x 186 = 372
Now, let’s determine if this number is a multiple of 3. For this purpose, add the digits of the number 372 and see if the resulting number is divisible by 3. As 3 + 7 + 2 = 12, hence the number 372 is also a multiple of 3 as evident from the multiplication shown below:3 x 124 = 372
Hence, the number 372 is a multiple of both 2 and 3.Example 2
List down the even factors of 150.Solution
The even factors of 150 are those numbers that are divisible by 2 so the even factors of the number 150 are given below:Even Factors of 150 = 2, 6, 10, 30, 50, and 150
All images/mathematical drawings are created with GeoGebra.