JUMP TO TOPIC
Factors of 44: Prime Factorization, Methods, Tree, And Examples
The factors of 44 are the numbers that give 44 as the result when these two numbers are multiplied together. The two numbers are said to form a factor pair. The factors of 44 can also be considered as those numbers that leave zero as the remainder when 44 is divided.
Figure 1 – All possible Factors of 44
What Are the Factors of 44?
The factors of 44 are 1, 2, 4, 11, 22, and 44. These numbers yield zero as the remainder and a whole number quotient when they act as the divisors for the number 44.The number 44 has 6 factors in total. These 6 factors form 3 factor pairs with one another.How To Calculate the Factors of 44?
You can calculate the factors of 44 by using the division method. The essential condition for this technique is that if a number leaves zero as the remainder and a whole number quotient when it acts as the divisor, then the number is said to be a factor.Division
Before implying the division method on the number 44, let’s first determine the range in which these factors lie. Since countless possibilities exist for numbers to be factors, it’s best to narrow them down.The range of the factors begins from the minor factor to the number, which is half of the original number. In this case, the actual number is 44, and its half is 22. So this indicated that the range of the factors of 44 would lie between 1 and 22. Furthermore, upon analyzing the number 44, it is quite evident that the number 44 is an even number. This automatically indicates that 2 is a factor of 44. The division of 44 from 2 is shown below:\[ \frac{44}{2} = 22 \]As a whole number quotient is produced, the number 2 is a factor of 44. Some additional factors of 44 are shown below:\[ \frac{44}{1} = 44 \]\[ \frac{44}{2} = 22 \]\[ \frac{44}{4} = 11\]\[ \frac{44}{11} = 4 \]\[ \frac{44}{22} = 2 \]\[ \frac{44}{44} = 1 \]So the factors of 44 are:Factors of 44: 1, 2, 4, 11, 22, 44These factors can be negative as well. Negative factors are the same as positive factors. The only difference between the two is the sign. Negative symptoms accompany negative factors.The negative factors are given below:Negative Factors of 44: -1, -2, -4, -11, -22, -44Factors of 44 by Prime Factorization
The prime factorization technique is used to determine the prime factors of a number. The prime factors for any number are those factors that are also the prime numbers. The process of division in prime factorization is carried out with the help of prime numbers.The division begins with the number itself and this number acts as the dividend for a respective prime number. The whole number quotient produced from this division then acts as the dividend in the next step.This process of division is repeated until 1 is achieved at the end. The prime factorization for the number 44 is shown below:44 $\div$ 2 = 22
22 $\div$ 2 = 11
11 $\div$ 11 = 1
This prime factorization can be mathematically expressed as follows:Prime Factorization of 44 = 2 x 2 x 11
ORPrime Factorization of 44 = $2^{2}$ x 11
The prime factorization of the number 44 is also shown below in figure 1: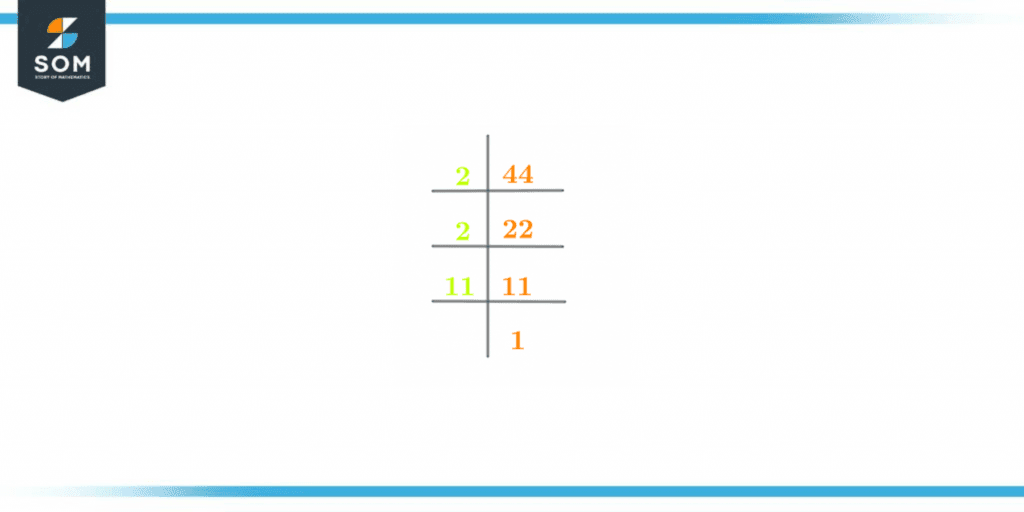
Figure 2 – Prime Factorization of 44
Factor Tree of 44
The factor tree is a visual representation of the number’s prime factorization. In other ways, a factor tree can be considered a technique that pictorially depicts the prime factors for any number.Just like prime factorization, the factor tree begins with the number itself. This number then splits into branches holding a whole a number quotient and a prime factor. The process is repeated until only prime factors are left at the end branches.The factor tree for the number 44 is shown in the figure below: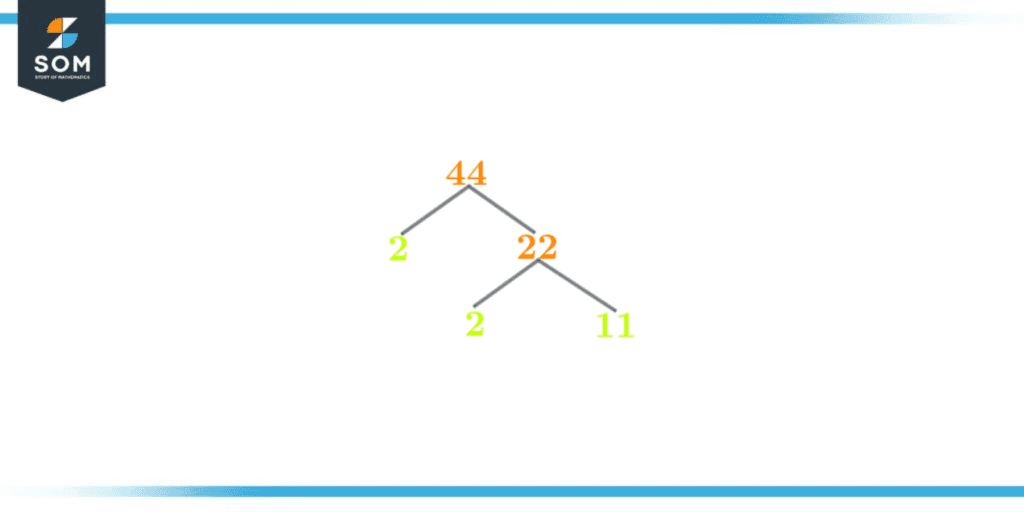
Figure 3 – Factor Tree of 44
Factors of 44 in Pairs
The factors of the number 44 can also exist in the form of factor pairs. A factor pair consists of two numbers that produce the original number when they are multiplied together. The number 44 has a total of 6 factors, so these 6 factors can be divided into 3-factor pairs. The only condition is that the product of the two numbers within a pair must be equal to 44. The factor pairs of 44 are given below:1 x 44 = 44
2 x 22 = 44
4 x 11 = 44
Hence, the factor pairs:Factor Pairs of 44 = (1, 44), (2, 11), and (4, 11)These factor pairs can be negative as well. The only requirement for negative factor pairs is that both the numbers within a pair must have a negative sign so that they can yield a positive product when they are multiplied together. The negative factor pairs are given below:-1 x -44 = 44
-2 x -22 = 44
-4 x -11 = 44
Negative Factor Pairs of 44 = (-1, -44), (-2, -11), and (-4, -11)Finding the Total Number of Factors
Sometimes we may encounter a problem in which we are required to find the total number of factors existing for a number, including both positive and negative factors. For such a scenario, the method described below comes in handy.To determine the total number of factors existing for a number, firstly attempt factorization on that number. For instance, the factorization of 44 is given below:Factorization of 44 = 1 x $2^{2}$ x 11
Next, add 1 to the exponents of all the factors after factorization and multiply them together. Adding 1 to the exponents of all the factors mentioned above in factorization and then multiplying them together yields a result of 12.This indicates that the number 44 has a total of 12 factors, 6 of which are positive factors and 6 of them are negative factors. So the total factors of 44, including both positive as well as negative, are shown below:Total Factors of 44 = 1, -1, 2, -2, 4, -4, 11, -11, 22, -22, 44, and -44Factors of 44 Solved Examples
The concept of factors of a number is fun and easy to learn. To further strengthen the idea of the factors of 44, given below are a few solved examples involving the factors of 44.Example 1
Determine the sum of all the factors of 44 and determine if the resulting number is a multiple of 2 or 3.Solution
To begin with, the solution of this example, let’s first list down all the factors of 44.Factors of 44 = 1, 2, 4, 11, 22, 44Now, calculating the sum of these factorsSum of factors of 44 = 1 + 2 + 4 + 11 + 22 + 44
Sum of factors of 44 = 84
Since the resulting number obtained is an even number, so that indicates that this number is a multiple of 2, as evident from the multiplication shown below:2 x 42 = 84
The number 84 is also a multiple of 3, which is evident from the sum of the digits of 84. As 8 + 4 = 12, which indicates that the number 12 is a multiple of 3, the number 84 is also a multiple of 3.3 x 28 = 84
Hence, the result obtained from calculating the number of factors of 44 is a multiple of 2 and 3.Example 2
Calculate the average of all the factors of 44.Solution
For calculating the average of the factors of 44, let’s first list down these factors. These are given below:Factors of 44 = 1, 2, 4, 11, 22, 44Now, calculating their average:\[ Average = \frac{\text{Sum of all the factors}}{\text{Total number of factors}} \]\[ Average = \frac{1 + 2 + 4 + 11 + 22 + 44}{6} \]\[ Average = \frac{84}{6} \]Average = 14
So the result states that the average of all the factors of 44 is 14. All the images/mathematical drawings are created with GeoGebra.