JUMP TO TOPIC
Factors of -6: Prime Factorization, Methods, Tree, and Examples
The factors of -6 are all those numbers by which -6 can be divided equally. The numbers that can split an original number evenly are called factors.
Additionally, when two integers are multiplied together to yield the number -6 as a result, they are referred to as the pair factors of the -6.

Figure 1 – All Factors of -6
As an illustration, the factor pairs for -6 are represented by the symbols (1,-6) and (-1,6). The original number should be produced when we multiply a pair of elements. For example, if we multiply -1 by 6, we get -6. As a result, we can take into account both positive and negative factor pairs of 6.
We shall employ the factorization method to discover the factors of the number -6. In the factorization method, the numbers 1 and -6 are taken as factors of -6 first. Then, the other pair of multiples of -6 are found, and the result is returned as an original number.
Read the article below to find factors of -6 in pairs as well as the division method to find the prime factors of -6 to better comprehend this strategy.
What Are the Factors of -6?
The factors of -6 are 1, -1 2, -2, 3, -3, 6, and -6 as they evenly divide -6 without any remainder.
The factors of -6 are the numbers that divide -6 perfectly without leaving a residual. In other words, the pairs of numbers that when multiplied together provide the original number -6 are the factors of -6.
How To Calculate the Factors of -6?
You can calculate the factors of -6 by discovering and compiling a list of all the factors of -6 and examining every number up to and including -6. The numbers that are completely divided by -6 leaving no remainder are considered to be its factors.
The factors of -6 can be found as:
-6 $\div$ 1= -6
-6 $\div$ 2= -3
-6 $\div$ 3= -2
6 $\div$ -1= -6
6 $\div$ -2= -3
6 $\div$ -3= -2
So, the factor list of -6 is given as:
Factor List: 1, -1, 2, -2, 3, -3, 6, and -6.
-6 is a negative integer therefore it can have both positive as well as negative factors with the condition that their multiplication in pairs will always result in a negative 6. Let us explore some interesting facts about number -6.
Important Properties
Following are some important facts about -6 that help in determining its factors.
- -6 is a negative integer.
- 6 is a composite number therefore it has more than 2 factors.
- It is an even number so 2 is the factor of -6.
- -6 is also the multiple of 3 therefore 3 is also its factor.
- The factors of -6 are not in the form of decimals or fractions.
- The total number of factors of -6 is 8 including the negative as well as the positive factors.
Factors of -6 by Prime Factorization
The prime factorization of -6 is given as (-2 x 3 = -6)
Finding the prime numbers that are multiplied together to produce the original number is the process of prime factorization.
Note that while every occurrence of a particular prime factor is included in the prime factorization of -6, the number 1 is excluded.
Identifying or finding the group of prime numbers that, when multiplied together, result in the original number -6 is known as the prime factorization or integer factorization of -6. This is also referred to as -6 prime decomposition.
Prime Factorization of -6 is the process of locating the prime factors of -6. Divide -6 by the smallest prime number you can find to obtain the prime factors of -6. The next step is to divide the outcome by the smallest prime integer. Continue doing this until you have 1.
The prime factorization -6 is shown below in figure 1:
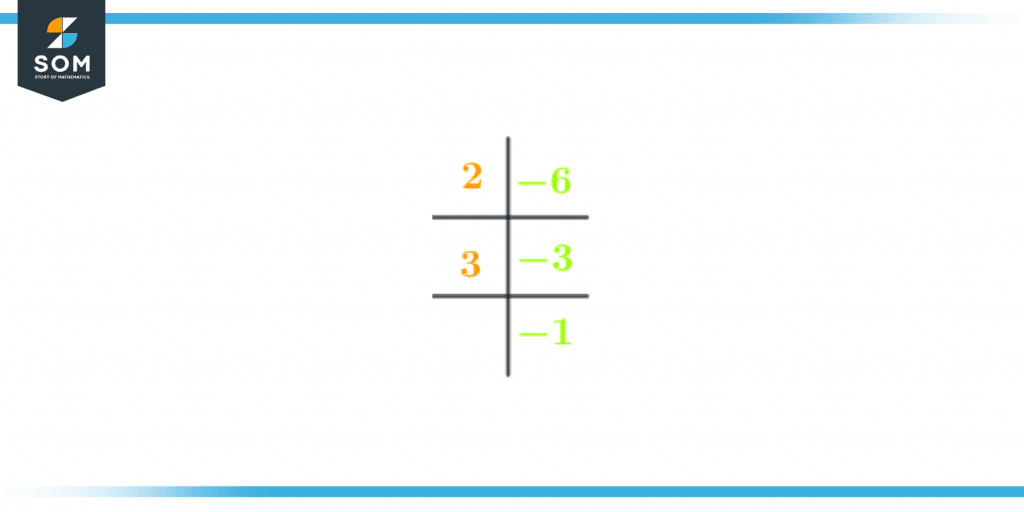
Figure 2 – Prime factorization of -6
Factor Tree of -6
The factor tree of -6 is shown below in figure 2:
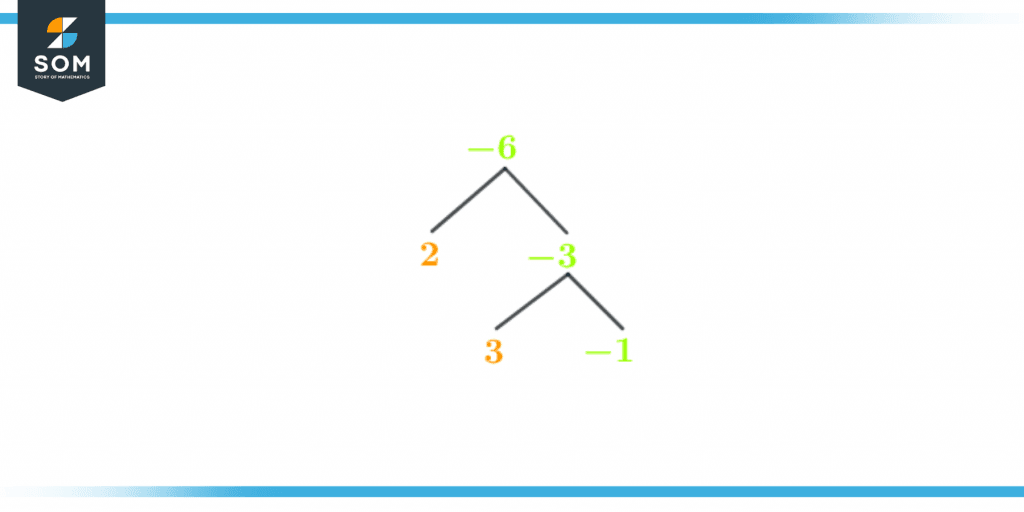
Figure 3 – Factor tree of -6
The factor tree is the pictorial description of prime factors decomposition of -6.
Factors of -6 in Pairs
Factor pairs of -6 are those numbers that when multiplied together give -6 as the result.
We must first obtain all of the factors of -6 to calculate the factor pairs of -6. Once you have a list of every one of those factors, you can pair them together to create a list of every pair of factors.
The factor pairs of -6 are determined as follows:
1 x −6 = −6
2 x −3 = −6
6 x −1 = −6
−1 x 6 = −6
−2 x 3 = −6
So, the factor pairs of -6 are given as:
(1,−6)
(−1,6)
(−2,3)
(−3,2)
Factors of -6 Solved Examples
Here are some solved examples incorporating factors of -6.
Example 1
What are the common factors between -6 and 8?
Solution
First, list factors of-6 and 8.
The factors of -6 are listed as -6, -3, -2, -1, 1, 2, 3, and 6
and the positive and negative factors of 8 are -8, -4, -2, -1, 1, 2, 4, and 8
Now identify the factors shared by both -6 and 8; these will be common factors between -6 and 8.
Therefore, -1, -2, 1, and 2 are the common factors between -6 and 8.
Example 2
Jimmy’s factor for the number -6 is (-2). How will he obtain the second factor?
Solution
The factor equation can be written as:
−6 = −2 x factor
So, the second factor will be given as:
−6 −2 = factor
Factor = 3
The second factor is therefore 3.
Example 3
Find the greatest common factor between -6 and 12?
Solution
First, list factors of-6 and 12.
The factors of -6 are listed as -6, -3, -2, -1, 1, 2, 3, and 6
and the factors of 12 are 1, 2, 3, 4, 6 and 12
the common factors between -6 and 12 are 1, 2, and 3 and from these, the greater common factor is 3
so therefore the greatest common factor between -6 and 12 is 3
Example 4
What are the common factors between -6 and 20?
Solution
First, list factors of 6 and 20.
The factors of -6 are listed as -6, -3, -2, -1, 1, 2, 3, and 6
and the positive and negative factors of 20 are -20, -10, -5, -4, -2, -1, 1, 2, 4, 5, 10 and 20.
Now identify the factors shared by both -6 and 20; these will be common factors between -6 and 20.
Therefore, -1, -2, 1, and 2 are the common factors between -6 and 20.
Images/mathematical drawings are created with GeoGebra.
