What Is 1 1/2 as a Decimal + Solution With Free Steps
 The fraction 1 1/2 as a decimal is equal to 1.5.
The fraction 1 1/2 as a decimal is equal to 1.5.
As we can see, a fraction has two parts: one bottom part and one top part. The upper part is called the numerator, and the bottom part is called the denominator.
The denominator is the total value of equal parts into which the whole is divided, and the numerator is the number of equal parts which have been taken out or which have been left out. And the denominator in a fraction cannot be zero because we cannot divide anything by zero.
A whole number and a fraction that is combined into one mixed number is called a mixed fraction.
Here, we can use the long division method to solve 1 ½ fractions.
Solution
To start, we multiply the given mixed fraction 1 1/2, which has a denominator of 2, by the whole integer 1, and then add a nominator 1, which happens to be equal to 3/2. This produces an existing simple improper fraction.
\[ 1 + \frac{1}{2} = \frac{3}{2}\]
We can now start to solve a current fraction into an actual division because we have changed the specified mixed fraction into an existing simple improper fraction. The numerator and denominator are equal to the dividend and the divisor, respectively, at the same time that we are familiar with this. As a result, we define our fraction at the following time:
Dividend = 3
Divisor = 2
After reviewing the division of this fraction, 3/2, we have given the outcome the term quotient.
Quotient=Dividend $\div$ Divisor = 3 $\div$ 2
Here, we use the mathematical long division method to find the solution to this fraction.
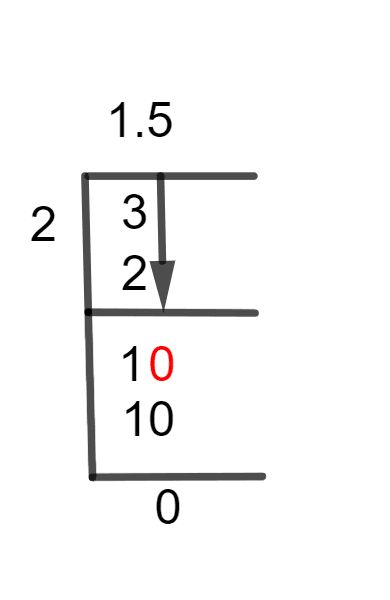
Figure 1
1 1/2 Long Division Method
We had:
3 $\div$ 2
By multiplying the dividend by 10, we can add a decimal point when the dividend is less than the divisor. We don’t need any decimal points when the divisor is lower, so 3/2 is divided as indicated in the example below.
3 $\div$ 2 $\approx $ 1
Where:
2 x 1 = 2
We left with the remainder, which is equal to 3 – 2 = 1.
At the time where we evaluate dividend 1 as well as find that it happens to be less than divisor 2, we are going to need to raise it. We already know that, in these circumstances, we apply the first rule that belongs to long division as well as multiply the dividend by 10.
The quotient now has 0 full types as well as no decimal numbers, with the exception that it also now has an existing decimal element. Therefore, the dividend is going to rise to 10. The answer happens to be:
10 $\div$ 2 = 5
Where:
5 x 2 = 10
If there happens to be no remainder left, then an existing 1.5 quotient happens to be obtained.
Images/mathematical drawings are created with GeoGebra.
