What Is 1 1/3 as a Decimal + Solution With Free Steps
 The fraction 1 1/3 as a decimal is equal to 1.333.
The fraction 1 1/3 as a decimal is equal to 1.333.
In a complex fraction, a fraction can be found in either the numerator or the denominator. A suitable fraction has a numerator that is less than its denominator.
It can also be stated as a mixed number, which is a whole-number quotient with a proper-fraction remainder, and is known as an improper fraction if the numerator is larger a repeating decimal, also known as a recurring decimal, is used to represent a number whose digits are periodic, repeating their values at regular intervals, and whose indefinitely repeated part is not zero.
To solve the 1 1/3 fraction, the long division method is recommended.
Solution
The provided mixed fraction 1 1/3 is first converted into an existing simple improper fraction by multiplying the denominator 3 by the whole number 1, and then by adding a nominator 1 that happens to be equal to 4/3.
\[ 1 + \frac{1}{3} = \frac{4}{3}\]
To continue, we, first of all, take the dividend and the divisor from our given fraction. The steps are as follows:
Dividend = 4
Divisor = 3
Recognizing that the denominator is the Divisor and the numerator is the Dividend. We may now go to the quotient, which is referred to as the solution to a division, with ease. Therefore, a quotient would appear as follows given the circumstances:
Quotient=Dividend $\div$ Divisor = 4 $\div$ 3
Here, we take the long division method to solve this fraction 4/3
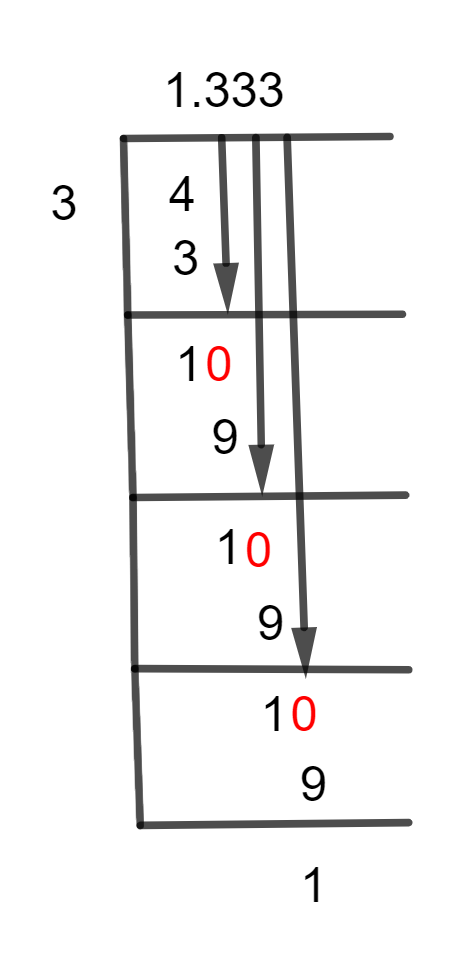
Figure 1
1 1/3 Long Division Method
We have fractions:
4 $\div$ 3
We need to add a decimal point when the dividend is less than the divisor, which we may do by multiplying the dividend by 10. Therefore, we don’t require any decimal points if the divisor is lower. 4/3is divided as illustrated in the instance below.
4 $\div$ 3 $\approx$ 1
Where:
3 x 1 = 3
4 – 3 = 1 is the remainder left after division.
Now we have dividend 1 and the divisor is 3 which means we have to multiply the dividend by 10 as it is smaller than the divisor.
10 $\div$ 3 $\approx$ 3
Where:
3 x 3 = 9
We are left with the remainder of 10 – 9 = 1
Our division is incomplete yet. we can see that remainder 1 need zero to solve further after multiplying remainder 1 with 10 our dividend becomes 10 And the divisor is 3.
10 $\div$ 3 $\approx$ 3
Where:
3 x 3 = 9
Again the remainder is 10 – 9 = 1
As the remainder is 1, again it will become 10 and we will divide it by 3.
10 $\div$ 3 $\approx$ 3
Where:
3 x 3 = 9
Again the remainder is 10 – 9 = 1
As this is a recurring number, after three iterations we stop here with remainder 1 and a quotient of 1.333 obtained.
Images/mathematical drawings are created with GeoGebra
