What Is 1/12 as a Decimal + Solution With Free Steps
 The fraction 1/12 as a decimal is equal to 0.083.
The fraction 1/12 as a decimal is equal to 0.083.
The division method is one of the four primary mathematical operations, and it does seem to be the trickiest one. As we know, when dealing with integers we come across divisions that don’t result in Integers, and thus have to be expressed as Fractions.
Fractions corresponding to a division result in a decimal value, and thus their solution lies somewhere between two integers. Decimal Numbers have two parts a whole number and the decimal number. Where the Whole Number is associated with an integer, and the Decimal Number is associated with a number smaller than 1.
Here we will go through the solution of our fraction 1/12, which is solved using the Long Division Method. The method used for solving fractions results in Decimal Values.
Solution
To solve the division between two numbers involved in a Fraction, we must first convert the numbers into the components of a division. As we know, the numerator is interchangeable with the Dividend, and the denominator is interchangeable with the Divisor, so we have the following:
Dividend = 1
Divisor = 12
We can understand more about the dividend and divisor’s Relationship by looking at it a certain way. This means that our dividend of 1 is to be divided into 12 parts, and one of those pieces is represented by the fraction given to us. This will thus be represented by the Quotient in our division:
Quotient = Dividend $\div$ Divisor = 1 $\div$ 12
As we know, we can solve such a division using Long Division Method. Let’s look at the solution to this problem:
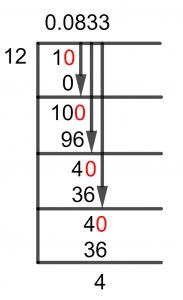
Figure 1
1/12 Long Division Method
The Long Division Method is the method used for solving a fraction into a decimal number. Thus, we start by first solving for a dividend that is not a Multiple of the divisor. The divisor is therefore used for finding the multiple Closest to the dividend.
This multiple is then subtracted from the dividend, and that makes the Remainder. The Remainder afterward becomes the new dividend, and then as it would be smaller than the divisor in most cases, we introduce the Decimal Point.
Now, as our dividend 1 is smaller than the divisor 12, we then multiply it by 10 to make it bigger than the divisor. As we can see, 10 will be smaller than 12, so we get:
10 $\div$ 12 $\approx$ 0
Where:
12 x 0 = 0
Hence, a remainder of 12 – 0 = 0 is generated, thus we repeat the process:
100 $\div$ 12 $\approx$ 8
Where:
12 x 8 = 96
Which produces a remainder of 100-96=0, hence we solve for 40 now:
40 $\div$ 12 $\approx$ 3
Where:
12 x 3 = 36
Hence, we get a repeating remainder equal to 4 and a Quotient that involves the repeating decimal of 3 as 0.083.
Images/mathematical drawings are created with GeoGebra.
