What Is 1/7 as a Decimal + Solution With Free Steps
 The fraction 1/7 as a decimal is equal to 0.142857.
The fraction 1/7 as a decimal is equal to 0.142857.
We use Fractions to express decimal numbers in terms of integers. As we know, Decimal Numbers cannot be expressed as integers, as they lie between two. So, how do we convert a fraction which contains two integers in a division into a Decimal Number?
The answer is simple, we use a method called Long Division. This method makes solving Problems of a such sort straightforward. A Decimal Number is composed of two components, one is the Whole Number, and the other one is the Decimal component.
So now let’s solve this problem using the Long Division Method and find its solution.
Solution
We solve fractions into decimal numbers by first transforming them into Division. As we know, a fraction represents a division, we can also Interchange the components of a fraction with that of a division. This is done by replacing the label of the numerator with Dividend, and the denominator with Divisor. It can be seen done down here:
Dividend = 1
Divisor = 7
Now, the quantity named the Quotient is of great importance here, as it is produced as a result of the division between two numbers. Thus, for our Fraction expressed as 1/7, we will express the Quotient as:
Quotient = Dividend $\div$ Divisor = 1 $\div$ 7
Finally, let’s go through the Long Division Solution to this problem:
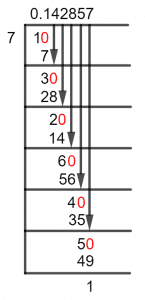
Figure 1
1/7 Long Division Method
To solve a problem by this method, we rely on the Multiple of the divisor, which is closest to the dividend. But that’s not all, when our dividend becomes Smaller than the divisor, we multiply it by ten and place a Decimal Point in the quotient.
Now we will introduce the last quantity of our interest, which is the Remainder. This is produced by Subtracting the multiple from the dividend. Also, this remainder becomes the Dividend after every iteration of the division.
Hence, looking at our dividend of 1, we see that it is smaller than the divisor, so we multiply it by ten, and place a Decimal in the quotient. This makes our dividend equal to 10, so let’s solve for 10/7:
10 $\div$ 7 $\approx$ 1
Where:
7 x 1 = 7
This leads to the generation of a Remainder equal to 10-7=3, so we repeat the process and get our new Dividend of 3 up to 30. Now, solving for 30/7 leads to:
30 $\div$ 7 $\approx$ 4
Where:
7 x 4 = 28
This then produces a Remainder of 30-28=2, which calls for us to repeat the process. And this time, we have 20/7 to solve:
20 $\div$ 7 $\approx$ 2
Where:
7 x 2 = 14
Hence, we finally have a remainder of 20-14 = 6. We usually would stop right here as we have a value until the Third Decimal Place, but if we keep solving it to the sixth decimal place, we find that this Quotient will repeat itself, so we have 0.142857.
Images/mathematical drawings are created with GeoGebra.
