What Is 1/4 as a Decimal + Solution With Free Steps
 The fraction 1/4 as a decimal is equal to 0.25.
The fraction 1/4 as a decimal is equal to 0.25.
A Fraction is a name for the mathematical expression of something being divided into equal parts or sections. The Denominator and the Numerator are the two parts of a fraction. Usually, solving fractions using multiples other than their fractional representations is challenging, but turning them into Division is a simple solution.
So, instead of using the Multiples method, we can solve these fractions using the Long Division method and receive the outcome in decimal values.
Here, the fraction 1/4 is solved by the method of Long Division to obtain its decimal value.
Solution
To begin with, we first have to divide the fraction. Division is the reverse of multiplication and Dividends and Divisors are two of the terms used to describe it. The term divisor refers to the number that divides the dividend, which is also a number. In the fraction 1/4, 1 is a dividend, while 4 is a divisor.
Dividend = 1
Divisor = 4
Quotient and Remainder, two further division-specific concepts, can now be used. The final answer which we get from the division is called a Quotient. It can be stated as follows:
Quotient = Dividend $\div$ Divisor = 1 $\div$ 4
The remainder, on the other hand, stands for a quantity that is left over after incomplete or partial division.
Below are detailed instructions for utilizing the Long Division method to solve the fraction of 1/4.
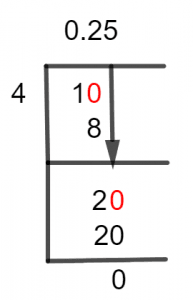
Figure 1
1/4 Long Division Method
The complete procedure to solve fraction 1/4 is shown below.
1 $\div$ 4
While solving a division problem, we see which one is smaller among the Divisor and Dividend. if the dividend is smaller than the divisor, we plug in a zero to the right of the dividend and have a Decimal Point in the Quotient.
In this question, 1 is the dividend, and 4 is the divisor. As 4 is greater than 1, we use a decimal point and place a zero to the right of 1, which makes it 10. Now, it can be solved as:
10 $\div$ 4 $\approx$ 2
Where:
4 x 2 = 8
The Remainder can be found as:
10 – 8 = 2
As we have a non-zero value of the Remainder, we need to solve it further to have complete results. Thus, we again place a zero to the Remainder’s right but don’t use any decimal point this time, because there is already a decimal value in Quotient. The remainder becomes 20. A further solution is given as:
20 $\div$ 4 $\approx$ 5
Where:
4 x 5 = 20
The Remainder is given as:
20 – 20 = 0
This time, the Remainder is 0. It means that the fraction is solved completely and we don’t need to solve further. We have 0.25 as a Quotient.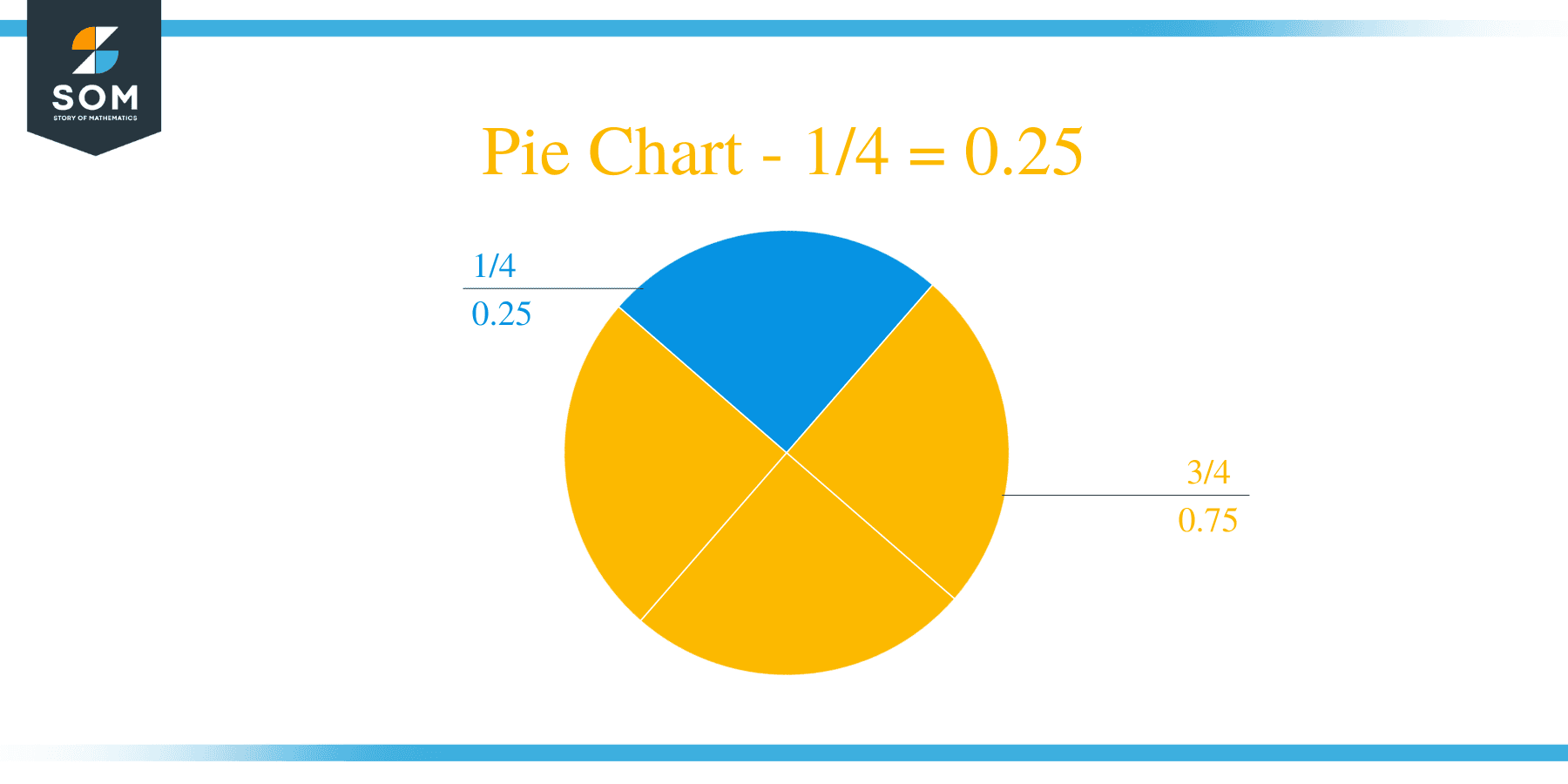
Images/mathematical drawings are created with GeoGebra.
