What Is 3/4 as a Decimal + Solution With Free Steps
 The fraction 3/4 as a decimal is equal to 0.75.
The fraction 3/4 as a decimal is equal to 0.75.
A Fraction is very commonly used for describing a division-based relationship between two numbers, but these numbers have to be from different Multiplicative families. This means that fractions are only valid for a denominator that is not a factor of the numerator.
This kind of Division Operation between numbers is therefore capable of being solved into a singular number, but that number would be a Decimal Number. So, to convert a fraction into a decimal number, we use a method called Long Division.
Now, let’s go through the Solution of our fraction 3/4 getting converted into a decimal number.
Solution
The first thing to do when solving a fraction to get a Decimal Value from it is to convert the fraction numbers into dividing numbers. This is done by comparing the Components of a fraction with that of a division.
Thus, the numerator becomes the Dividend, and the denominator becomes the Divisor:
Dividend = 3
Divisor = 4
Here, we will introduce the quantity, Quotient, which represents the resulting solution to a division. A Quotient is directly dependent on the Dividend and the Divisor, and their relationship in our case is expressed as follows:
Quotient = Dividend $\div$ Divisor = 3 $\div$ 4
Hence, we look at the Long Division solution to our problem given as:
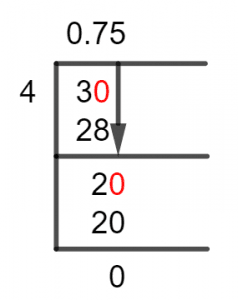
Figure 1
3/4 Long Division Method
The Long Division Method is known for solving its problems using the process of division in parts. We introduce a Decimal Point into the quotient based on the fraction’s numerator or in our case the division’s dividend. If the dividend is smaller than the divisor, then we place it at a decimal point and multiply the dividend by the number 10.
Now we also introduce the quantity known as the Remainder, it is the number left behind after an iteration of Division is done. But it is also the number that becomes the new Dividend in the next iteration.
Finally, a Remainder is produced because when the divisor is not a factor of the dividend, the closest multiple of the divisor to the dividend is then subtracted from the dividend. This subtraction then produces a Remainder.
So, as our dividend is 3 smaller than 4, we multiply it by 10, and solve:
30 $\div$ 4 $\approx$ 7
Where:
4 x 7 = 28
Which produces a remainder equal to 30 – 28 = 2, now we repeat the process as we got a dividend 2 smaller than 4 to multiply it by 10:
20 $\div$ 4 = 5
Where:
4 x 5 = 20
This produced no Remainder, which means that the divisor 4 is a factor of the dividend 20. Now, we compile the quotient, as we multiplied our Dividend 3 by 10 it placed a decimal value in our Quotient with the whole number 0.
So, the finalized Solution to our problem is 0.75 once all pieces of the division are stitched together.
Images/mathematical drawings are created with GeoGebra.
