What Is 2/3 as a Decimal + Solution With Free Steps
 The fraction 2/3 as a decimal is equal to 0.666.
The fraction 2/3 as a decimal is equal to 0.666.
Fractions are widely known for expressing the operation of division occurring between two numbers, but they represent a very special kind of division. This Division cannot be solved using the traditional method and thus requires a new technique.
This new technique is called the Long Division Method, and it is known for solving division problems in pieces. Solving a problem using this method leads to a Decimal Value to be produced as its result.
Now, let’s take a deeper dive into the solution of our fraction 2/3.
Solution
The first step in solving a problem such as 2/3 into a Decimal Value is that we separate the constituents of the fraction and convert them into the Division components. This is done by transforming the numerator into the Dividend and the denominator into the Divisor.
This is done as follows:
Dividend = 2
Divisor = 3
This is when we introduce the quantity known as the Quotient, it represents the solution to a division problem. And we find it by applying the Division operation between the two numbers referred to as Dividend and the Divisor:
Quotient = Dividend $\div$ Divisor = 2 $\div$ 3
Now, to find out the Quotient of this fraction transformed into a division; we shall solve this problem using the Long Division Method:
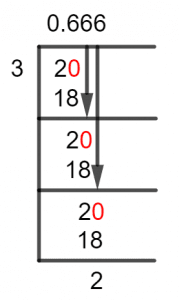
Figure 1
2/3 Long Division Method
We start by understanding the process of Long Division, it works by placing a decimal point after the Whole Number of the Quotient. Placing this Decimal Point gives us the ability to multiply 10 by every dividend.
The Whole Number in the Quotient is the number that corresponds to the non-decimal part of the Quotient so for a proper fraction it is 0 and for Improper, otherwise.
Finally, we have a Remainder produced after each division iteration, and this number then becomes the new Dividend to be solved in the next iteration. We run at least three iterations to get the most accurate result.
Taking a look at our numerator 2 we see that this is a proper fraction, and so we multiply the dividend with 10 and get 20. The Quotient now contains the 0 and the decimal point, and now we shall solve for this dividend:
20 $\div$ 3 $\approx$ 6
Where:
3 x 6 = 18
Hence, a Remainder of 20-18 = 2 is produced, and we repeat the process now 2 is the dividend and we multiply 10 with it and solve:
20 $\div$ 3 $\approx$ 6
Where:
3 x 6 = 18
Now, as we can see the Remainder is repeating itself, 20 – 18 = 2, this is a repeating decimal number, and the Quotient when compiled together results in 0.666. And it will keep repeating its value until infinity.
Images/mathematical drawings are created with GeoGebra.
