What Is 1/5 as a Decimal + Solution With Free Steps
 The fraction 1/5 as a decimal is equal to 0.2.
The fraction 1/5 as a decimal is equal to 0.2.
The mathematical representation of something that has been divided into two or more sections or parts is called a Fraction. There are two components of fraction, which are Denominator and Numerator. Usually, it is difficult to solve fractions using multiples other than their fractional representations. But an easy way is to transform them into division.
Here we use the method of Long Division to solve these fractions instead of the Multiples method. This method gives us the result in decimal values.
In this question, a fraction of 1/5 is solved using the method of Long Division, and its decimal equivalent is found.
Solution
To start, we first convert the fraction into a division. The opposite of multiplication is known as Division and its components include Dividends and Divisors. In the solution, we separate these components of division according to their operations and functions. A dividend is a number, that is being divided, while the number dividing the dividend is called the divisor. In the problem given, 1 is the dividend, and 5 is the divisor.
Thus, the given fraction can be written in the form of dividend and divisor as:
Dividend = 1
Divisor = 5
Now, two other division-specific terms Quotient and Remainder can be introduced. The quotient is the solution obtained as a result of division. It can be expressed as:
Quotient = Dividend $\div$ Divisor = 1 $\div$ 5
Whereas, Remainder represents a term that is left if the division is not done completely.
Complete steps to solve this fraction of 1/5 using the Long Division method are shown below.
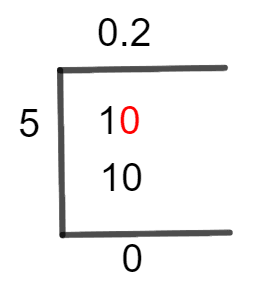
Figure 1
1/5 Long Division Method
The detailed steps of the Long Division are shown below.
We have to solve a fraction of 1/5.
1 $\div$ 5
The first step of long division is to check if the Divisor is greater than the Dividend. If the divisor is greater, we need to introduce a Decimal Point. For this purpose, we have to place a zero to the right of the dividend. However, if the dividend is greater, we don’t need any Decimal Point.
In the given problem, 1 is smaller than 5, which means Divisor is smaller than Dividend so, we need a Decimal Point to proceed further. To have a decimal point, we add a zero to the right of the dividend. When we add a zero to 1, it becomes 10.
Now, we solve as:
10 $\div$ 5 $\approx$ 2
Where:
5 x 2 = 10
To check the Remainder, we subtract the two values as shown below.
10 – 10 = 0
We get 0 remainders as a result of this division. It indicates that the fraction is solved completely and there is no need for further calculations. Quotient 0.2 is our final and accurate result of this division.
Images/mathematical drawings are created with GeoGebra.
