What Is 15/16 as a Decimal + Solution With Free Steps
 The fraction 15/16 as a decimal is equal to 0.9375.
The fraction 15/16 as a decimal is equal to 0.9375.
We are aware that fractions are of two types, one is Proper, and the other is Improper. A Proper Fraction is one where the numerator is smaller than the denominator, and the Improper is the one where the denominator is bigger than the numerator.
Both these fractions will result in a Decimal Value, but the improper one would produce a whole number bigger than 0. We have a fraction of 15/16 which is Proper, so it will produce a whole number of 0.
A Whole Number in a fraction is the non-decimal part of the fraction. Now, let’s look at the solution to our fraction in detail.
Solution
First, we take the Dividend and the Divisor out of our fraction:
Dividend = 15
Divisor = 16
Where a Dividend is a numerator being divided, and the Divisor is the denominator that divides.
Now, we move forward by introducing the Quotient, which is the result of a division. But for a fraction that cannot be solved further using the Multiple Method, we use another method. This method is called Long Division, and we begin by expressing our transformed fraction as a division:
Quotient = Dividend $\div$ Divisor = 15 $\div$ 16
Now, let’s dive deeper into the Long Division solution of the fraction 15/16:
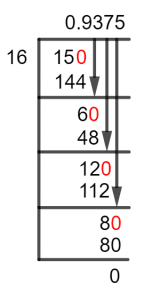
Figure 1
15/16 Long Division Method
We start by discussing the number called the Remainder, which is what remains when an Inconclusive Division occurs. It is important because it will become the new dividend as we move forward in solving the division.
Long Division generally works by introducing a Decimal Point in the Quotient, as our fraction is proper, it will do that from the start.
So, given that 15 is smaller than 16 we will introduce a zero to its right to make it into 150. Now, let’s solve it:
150 $\div$ 16 $\approx$ 9
Where:
16 x 9 = 144
Hence, a Remainder of 150 – 144 = 6 is generated. Now, we shall repeat the process and add another Zero to the dividend which is now 6 and it becomes 60. Solving for it result in:
60 $\div$ 16 $\approx$ 3
Where:
16 x 3 = 48
Which produces a Remainder of 12, now solving for this would lead to:
120 $\div$ 16 $\approx$ 7
Where:
16 x 3 = 112
Thus, we have a Remainder equal to 8. As we have gone through three iterations and produced a result up to Third Decimal Place, we can usually quit the process here. But if we look closely then we see that 8 would become 80, which is a Multiple of 16 so we can find the complete solution to this fraction.
80 $\div$ 16 $\approx$ 5
Where:
16 x 5 = 80
Thus, a viable Quotient is calculated, which is equal to 0.9375, with no Remainder.
Images/mathematical drawings are created with GeoGebra.
