What Is 5/7 as a Decimal + Solution With Free Steps
 The fraction 5/7 as a decimal is equal to 0.714.
The fraction 5/7 as a decimal is equal to 0.714.
We have all come across Fractions at some point in time as they are used for expressing a division operation between two numbers.
But some Fractions don’t solve completely and those result in Decimal Values, and here we are interested in solving for those.
To solve a division that is not conclusive, we use a method called Long Division so let’s look at the solution of our fraction 5 / 7.
Solution
First, we get started by getting the Dividend and the Divisor out of our fraction. This is done as follows:
Dividend = 5
Divisor = 7
Knowing that the numerator is the Dividend, and the denominator is the Divisor. Now, we can smoothly move on to the Quotient as well, which is defined as the solution to a division. So, a Quotient under the given circumstances would look like this:
Quotient = Dividend $\div$ Divisor = 5 $\div$ 7
Here, we have completely transformed the expression for the fraction, and now we are ready to solve this division using the Long Division Method.
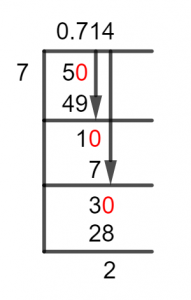
Figure 1
5/7 Long Division Method
We have a starting point here, and it is:
5 $\div$ 7
Now, this very expression can tell a lot about the nature of the Quotient. As it can be seen the dividend is smaller than the divisor, so the Quotient will be smaller than 1.
Finally, one last important piece of information is without a doubt the Remainder. The number will carry forward an Inconclusive Division, and also replace the dividend multiple times.
So, we have 5 smaller than 7 which tells us that we require to introduce a Zero to the right of the dividend, and hence a decimal point to the quotient. This leads to the dividend becoming 50, and its division is given below:
50 $\div$ 7 $\approx$ 7
Where:
7 x 7 = 49
Which will give us a remainder of 50 – 49 = 1.
Therefore, a Remainder of 1 was generated as a result of the incomplete division between our dividend and the divisor. And now it is time for the remainder to become the new dividend, we can see that 1 needs a Zero to be solved further. So, we get the new dividend as 10:
10 $\div$ 7 $\approx$ 1
Where:
7 x 1 = 7
Hence, we have 10 – 7 = 3 as the remainder.
It is common knowledge that the Division is carried out to the third decimal place for accuracy in case of no apparent complete solution. So, we repeat the process one last time, the dividend becomes 30.
30 $\div$ 7 $\approx$ 4
Where:
7 x 4 = 28
Thus, 30 – 28 = 2 is the remainder.
We conclude our efforts here, therefore we have a Quotient of 0.714 and a Remainder of 2 after three iterations.
Images/mathematical drawings are created with GeoGebra.
