What Is 3/16 as a Decimal + Solution With Free Steps
 The fraction 3/16 as a decimal is equal to 0.187.
The fraction 3/16 as a decimal is equal to 0.187.
Division seems the most difficult one among all mathematical operations. But actually, it is not that tough because there is a solution to deal with this challenging problem. The method for solving the question in fraction form is called Long Division.
Here is the complete solution to solve the given fraction i.e., 3/16 that will produce the decimal equivalent using the method called Long Division.
Solution
First, we will separate the constituents of the fraction depending on the nature of their operation. When a fraction is divided, the numerator is referred to as the Dividend and the denominator is known as Divisor, and this brings us to this result:
Dividend = 3
Divisor = 16
Now, we rearrange this fraction more descriptively by introducing the new term called Quotient, which is referred to as the result of the desired division.
Quotient = Dividend $\div$ Divisor = 3 $\div$ 16
Now, by using the Long Division method we can solve the problem by:
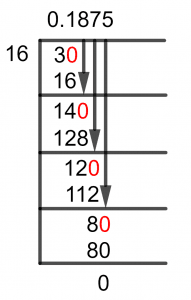
Figure 1
3/16 Long Division Method
You can take a closer look at the Long Division Method utilized to fix this issue by doing the following.
We had:
3 $\div$ 16
We already know that 16 is greater than 3, thus you can’t divide this number without using a decimal point. We now insert a zero to the right of our Remainder to add the desired decimal point.
Another division-specific term, Remainder, is used to describe the value that remains after an incomplete division.
Since 4 is a remainder in this situation, we shall add the Zero to its right, and convert 4 to 40 in the process. So now, we determine:
30 $\div$ 16 $\approx$ 1
Where:
16 x 1 = 16
This indicates that a Remainder was also generated from this division, and it is equal to 30 – 16 = 14.
We repeat the operation after having a remainder from the Division and add a zero to the Remainder’s right. Given that the Quotient is already a decimal value in this situation, we won’t need to add another decimal point.
As the remainder from the previous step was 14, so by adding a Zero to its right it will give us 140. Now we can further solve it as follow:
140 $\div$ 16 $\approx$ 8
Where:
16 x 8 = 128
So, after this, the Remainder is equal to 12. Bringing in another zero to its right will give 120, so we must calculate the following to solve to three decimal places:
120 $\div$ 16 $\approx$ 7
Where:
16 x 7 = 112
We have a resulting Quotient equal to 0.187 with a Remainder of 8. This indicates that if we continue to solve, we might be able to obtain a more precise result.
Images/mathematical drawings are created with GeoGebra.
