What Is 3/2 as a Decimal + Solution With Free Steps
 The fraction 3/2 as a decimal is equal to 1.5.
The fraction 3/2 as a decimal is equal to 1.5.
Decimal Numbers are unique as they represent values that lie between integers. Therefore, a decimal number contains two parts, one is the Whole Number representing the integer, and the other is the Decimal part which is present on top of the integer.
Now, we can also refer to the decimal part as a Fraction i.e., a small part of the bigger integer value. As we are aware, the decimal part of a decimal number is smaller than the Integer represented by 1. And so, fractions come into play when working with decimal numbers, as a fraction that doesn’t solve end to end will result in a Decimal Number.
Now, let’s go through the solution of our fraction to decimal Conversion for 3/2.
Solution
We begin by converting the Constituents of a fraction into the components of a division. We are aware that the numerator of a fraction is equivalent to the Dividend of a division, and the denominator is also referred to as the Divisor. So let’s transform the fraction into its corresponding division:
Dividend = 3
Divisor = 2
Looking at these Division Components, we can conclude that we are dividing 3 into 2 pieces and taking one of those pieces as a result of our division. And once we solve this division, we will acquire our Quotient, the number corresponding to the solution of a division.
This is mathematically expressed as:
Quotient = Dividend $\div$ Divisor = 3 $\div$ 2
Now, without further ado let’s look at the Long Division Solution of this fraction:
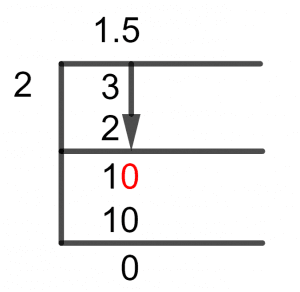
Figure 1
3/2 Long Division Method
The basic idea behind solving a division using the Long Division Method is to find the divisor’s Multiple, which has the closest value to the dividend. As we know that the dividend is not a Multiple of the divisor, we subtract the multiple from the dividend to find the difference, this is called the Remainder.
The second most important part of the Long Division Method is the transformation of the dividend in cases when it is smaller than the divisor. So if the Dividend is smaller than the divisor, then we multiply the dividend by 10 and introduce a decimal point in the Quotient.
Now, let’s take a look at the dividend we have, 3 which is bigger than 2 so, it’s an Improper Fraction. Moving forward, we will solve 3/2:
3 $\div$ 2 $\approx$ 1
Where:
2 x 1 = 2
Thus, a Remainder equal to 3 – 2 = 1 is produced. Now, we have to add a decimal point after 1 in the quotient, as 1 is smaller than 2. We now have 10/2:
10 $\div$ 2 = 5
Where:
2 x 5 = 10
Therefore, we finally have a solution to our problem, no Remainder is produced, and a Quotient with a Whole Number 1 is produced. Finalizing the Quotient produces 1.5.
Images/mathematical drawings are created with GeoGebra.
