What Is 3/20 as a Decimal + Solution With Free Steps
 The fraction 3/20 as a decimal is equal to 0.15.
The fraction 3/20 as a decimal is equal to 0.15.
A Fraction is a unit of measurement used to indicate how many identically sized components make up a whole. In a simple fraction, two integers, numerator and denominator are separated by a line, making it simple to identify. The number above the line is Numerator while below the line is Denominator.
We need to convert fractions into Decimals because it makes them easier and simpler to understand. Additionally, it is simple to tell which decimal number is larger and which is smaller by considering their decimal values. However, it is not easy while we are comparing two fractions.
In this example, the decimal value of 3/20 is found by using the Long Division method.
Solution
Before solving a fraction, it is necessary to identify whether it is a proper or improper fraction. If the denominator is a larger number than the numerator, the fraction is known as a Proper Fraction. On the other hand, if the numerator is larger, it is known as an Improper Fraction.
Now, to solve a fraction, we first convert it into Division. This is done by distinguishing its components based on their functions. The number to be divided is represented as a Dividend, while the number, which is dividing is referred to as a Divisor.
The other two important terms of the division include the Quotient, which is the final result obtained by dividing two numbers, and the Remainder, which represents the remaining value, that is left after an incomplete division. Any non-zero value of remainder at the end of division shows that divisor is not a factor of dividend.
The presented example can be stated mathematically as:
Dividend = 3
Divisor = 20
Quotient = Dividend $\div$ Divisor = 3 $\div$ 20
This fraction is solved using Long Division and the steps are shown below.
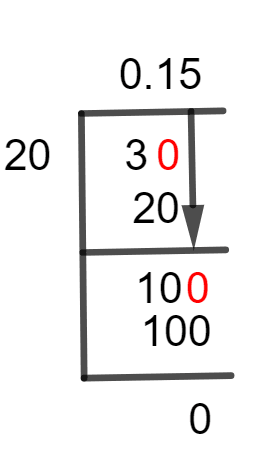
Figure 1
3/20 Long Division Method
Below is the explanation of steps to solve the 3/20 fraction.
3 $\div$ 20
As the divisor 20 in the given fraction is greater than dividend 3, so we have to introduce a Decimal Point by inserting a zero to the dividend’s right. Therefore, we get 30 by inserting a zero to the right of 3. Now, 30 is divided by 20 as shown below:
30 $\div$ 20 $\approx$ 1
Where:
20 x 1 = 20
The remainder is given below:
30 – 20 = 10
As a non-zero remainder is produced, so we again insert a zero to the right of the remainder, but without adding any decimal point. We get 100 now, which is to be divided by 20.
100 $\div$ 20 $\approx$ 5
Where:
20 x 5 = 100
The remainder is computed as:
100 – 100 = 0
This time, the Remainder is zero, which shows that the divisor and quotient are factors of the dividend. 0.15 is the calculated value of the Quotient.
Images/mathematical drawings are created with GeoGebra.
