What Is 3/6 as a Decimal + Solution With Free Steps
The fraction 3/6 as a decimal is equivalent to 0.5.
Fractions are used to describe how many parts of a certain size there are. For example, one-half means that the numerator (the number being divided) is half of the denominator while five-eights mean 5 out 8.

Fractions can also be described as a mathematics concept that deals with dividing one thing into another. It can be applied to any size or amount of equal parts, for example, 1/2 which represents half the size in comparison to an entire something.
A fraction is generally represented in the form of p/q where p is called the numerator and q is named as the denominator. If a numerator is completely divisible by a denominator it yields a whole number but if it is not completely divisible by it a decimal number is obtained.
Let us find out the solution to the given fraction with a detailed description.
Solution
In the given fraction, the numerator is smaller than the denominator, which means the result will be in the form of a decimal number. Let’s understand the various components of this division.
The numerator of the fraction is regarded as a dividend whereas the denominator is called the divisor. The result obtained is called the quotient and the remaining part obtained as a result of division is called the remainder.
Dividend = 3
Divisor = 6
The division can be represented as:
Dividend $\div$ Divisor = Quotient
The 0 remainder indicates that further division is not possible. The following graphical demonstration shows the division process to express 3/6 as a decimal.
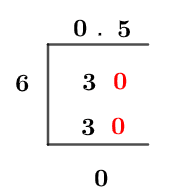
Figure 1
3/6 by Long Division Method
The above fraction is solved using the long division method. The long division method involves dividing the dividend by divisor such that further division is impossible.
Long division is a method for dividing large numbers without having perfect squares. The process starts by noting that the dividend will be reduced to some integer, and then you need to find another number that when multiplied with this original one gives an answer less than or equal to it but not greater.
Let’s express 3/6 in the form of division as given below:
3 $\div$ 6
Since 3 and 6 are multiple of 3 so it can be simplified as:
1 $\div$ 2
Now further simplification is not possible as the given fraction has been converted into its lowest form. Therefore for long division, the requirement is to make the dividend bigger than the divisor. For that add a decimal point in the quotient and zero with the dividend.
The division will produce:
1 $\div$ 2 = 0.5
The division is one of the most commonly used arithmetic operations that produce new numbers as a result of its operation. Division can be done for both proper as well as for improper fractions.
Therefore, the fraction 3/6 is equal to 0.5 with zero as a remainder.
Images/mathematical drawings are created with GeoGebra.
