What Is 4/15 as a Decimal + Solution With Free Steps
 The fraction 4/15 as a decimal is equal to 0.266.
The fraction 4/15 as a decimal is equal to 0.266.
Fractions describe dividing numbers, where one is being divided which is the Numerator and the other is the one doing the dividing, which is the Denominator.
But these divisions are stuck as they cannot be solved using Multiples beyond this fractional representation.
At this point, we move away from the method of multiples and use a different method called the Long Division to find the solution to a said fraction. This type of division results in Decimal Values.
So, let’s see what decimal value the fraction 4/15 solves up to.
Solution
We begin by transforming this fraction into a division, and divisions do not have numerators and denominators, rather they have Dividends and Divisors. So we can see them extracted from the fraction as follows:
Dividend = 4
Divisor = 15
Now, we introduce another term which is the Quotient, the resulting solution to a division, which can be generally expressed as:
Quotient = Dividend $\div$ Divisor = 4 $\div$ 15
The Quotient is what we are trying to find for the given fraction, and this Quotient relies heavily on the dividend and the divisor. It can be seen that our dividend of 4 is smaller than the divisor’s 15, and this would produce a Quotient that will have 0 as its whole number.
Therefore, the Decimal Value would be smaller than 1.
Now, we solve our problem using the Long Division Method as follows:
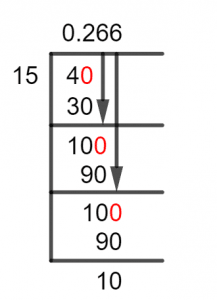
Figure 1
4/15 Long Division Method
As we are now solving a Long Division problem, we start by expressing our problem as a division:
4 $\div$ 15
We are aware of the value which remains as a result of an incomplete division, it is known as the Remainder. It is special as when we solve one iteration of the division, the remainder generated becomes the Dividend for the next iteration of the division process.
Therefore, a Long Division moves forward by introducing a decimal point to the Quotient while adding a Zero to the dividend, thus making it greater than the divisor.
Now, let’s look at the dividend 4 of our fraction, it is smaller than the divisor, so it requires a Zero to be added to its right, which makes it 40. Now, we can solve for 40/15:
40 $\div$ 15 $\approx$ 2
Where:
15 x 2 = 30
This produces a Remainder equal to 40 – 30 = 10, this remainder is therefore set up to become the new dividend. We can see that it is smaller than 15 so we introduce the Zero again and get 100. Now, solving for 100:
100 $\div$ 15 $\approx$ 6
Where:
15 x 6 = 90
The Remainder for which is again 10. Now, we can see a pattern, the Remainder repeats itself and so will the Quotient value, thus this is a Repeating Decimal Value.
The Quotient for this problem can be found as 0.266. Because we added a zero to the dividend, there is a decimal in the quotient. The Remainder is 10, which produces a repeating value of 6.
Images/mathematical drawings are created with GeoGebra.
