What Is 6/8 as a Decimal + Solution With Free Steps
 The fraction 6/8 as a decimal is equal to 0.75.
The fraction 6/8 as a decimal is equal to 0.75.
A Fraction is a mathematical representation to express how many parts of the same size make up the whole. It is made up of two integers written in the form of p/q. Here, p represents the Numerator and q represents the Denominator of the fraction, while the line between p and q indicates division.
Usually, fractions are converted into decimals because they are simpler to understand and solve. Furthermore, by comparing the decimal values of the two decimal numbers, it is easy to determine which is larger and which is smaller. But, when we compare two fractions, it is challenging.
In this question, a fraction of 6/8 is solved by the Long Division method to get its decimal value.
Solution
For solving a fraction first, we check whether it is a proper fraction or an improper fraction. A Proper Fraction contains a denominator greater than a numerator, while an Improper Fraction has a greater numerator as compared to a denominator.
To solve a fractional problem, it is converted into division. This is accomplished by classifying its elements according to how they operate. The numerator or number to be divided is referred to as the Dividend and the denominator or the divider is referred to as the Divisor.
After completing the division process, we get a Quotient, which is the final result of the division. However, if a division is not completed, we get a remaining value known as the Remainder.
In the fraction given in the question, 6 is the dividend, and 8 is the divisor as stated below.
Dividend = 6
Divisor = 8
Quotient = Dividend $\div$ Divisor = 6 $\div$ 8
Utilizing Long Division, this fraction is resolved to get its decimal value.
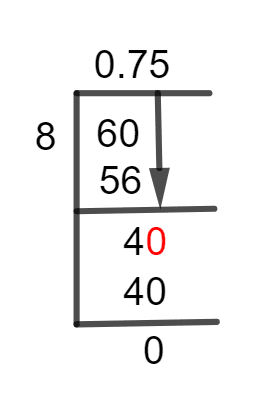
Figure 1
6/8 Long Division Method
A step-by-step explanation to solve the presented fraction is shown below:
We have:
6 $\div$ 8
It can be seen that the dividend is a smaller number as compared to the divisor. So, we require a Decimal Point, which can be obtained by adding a zero to the dividend’s right. While doing so, we get 60, which is to be divided by 8.
60 $\div$ 8 $\approx$ 1
Where:
8 x 7 = 56
The remainder is calculated to be 4:
60 – 56 = 4
This non-zero remainder shows that the fraction is not solved completely. Therefore, we once again add a zero to the remainder’s right. But now we don’t need to insert any decimal point. By inserting zero we get 40, which is divided by 8.
40 $\div$ 8 $\approx$ 5
Where:
8 x 5 = 40
The value of the remainder is:
40 – 40 = 0
Now, we get a zero as a Remainder, which indicates that the fraction is solved completely and Quotient 0.75 is the equivalent decimal number of this fraction.
Images/mathematical drawings are created with GeoGebra.
