Abscissa|Definition & Meaning

Definition

The abscissa is defined as the x-coordinate or horizontal axis of a point in a 2-dimensional plane of Cartesian coordinates. The abscissa is the length from the y-axis calculated parallel to the x-axis. The Abscissa is the x-coordinate in plane Cartesian coordinates of a point and it is the measure of the distance from the y-axis parallel to the x-axis. Astronomers and physicists often utilize the term abscissa to direct to the axis itself rather than the distance along it.

In common usage, the abscissa directs to the (x) coordinate. To denote the (y) coordinate the term ordinate is being used in standard two-dimensional plains. The terms Abscissa and ordinate help to explain the two-dimensional graphs.

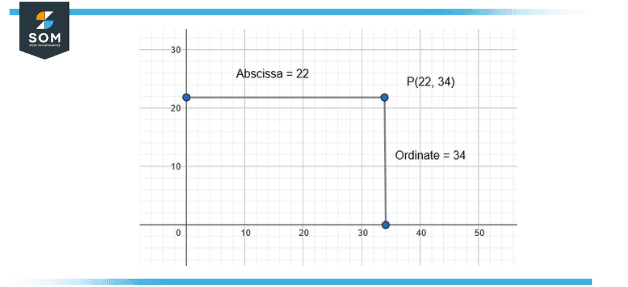
Figure 1 – Example of Abscissa and Ordinate.

Abscissa and Ordinate

The main difference between the abscissa and ordinate is that the abscissa refers to the y-axis and the ordinate refers to the y-axis. The detail of their differences is explained in the below paragraph. The abscissa is also called the x-axis of the point and is the distance of a point from the y-axis, rising with the x-axis. On the other hand, the ordinate which is also named the y-axis is the length of a point from the x-axis rising with the y-axis.

For instance, assume (x, y) is given as an ordered pair. Y is the ordinate, y-axis, or vertical axis here and similarly, x is the abscissa, x-axis, or horizontal axis here. An ordered pair is operated to indicate a point in the Cartesian plane and the first coordinate (x) in the plane is named the abscissa, and the second coordinate (y) in the plane is the ordinate.

The length of a point from the y-axis rising with the x-axis is named abscissa. In mathematics, the abscissa and the ordinate refer to the first and second coordinates of a point in a Cartesian coordinate system. Both the Abscissa and Ordinate define the locations of the point in the Cartesian two-dimensional plane. By using the abscissa and the ordinate a pattern or a trend of the data can also be extracted by looking at the points.

Understanding Abscissa Using Figures

We will illustrate the Abscissa and Ordinate using different graphs.

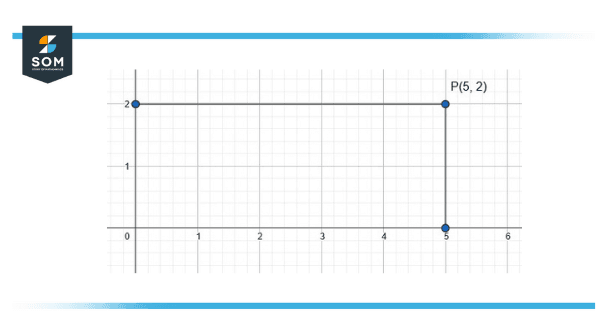
Figure 2 – The point (5, 2) in the cartesian plane

Figure 2 shows the two-dimensional graph, The horizontal axis is from the range 0 to +6 and whereas the vertical axis has a range from 0 to +2, There is a point located at the location (5, 2), The notation (5, 2) means that the point has abscissa of 5 and the ordinate of 2. Point (5, 2) has a distance of 5 from the origin on the x-axis and a distance of 2 from the origin on the y-axis.

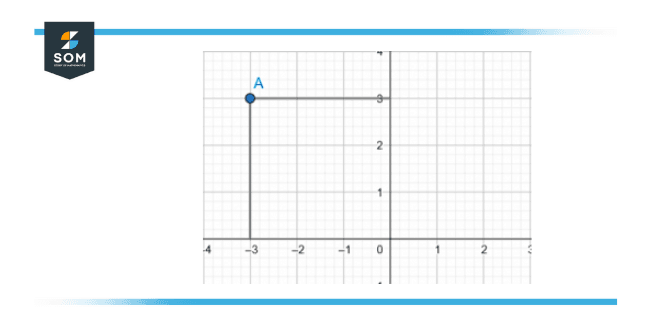
Figure 3 – The point (-3, 3) in the cartesian plane

Figure 3 shows the two-dimensional cartesian plane, The horizontal axis is in the range -4 to +3 and whereas the vertical axis has a range from 0 to +3, There is a point at the place (-3, 3), The inscription (-3, 3) means that the point has abscissa of -3 and the ordinate of 3. The point (-3, 3) has a distance of -3 from the origin on the x-axis and a distance of 3 from the origin on the y-axis.

Further Explanation: Abscissa and Data Representation

The abscissa is a term related to a two-dimensional graph and the goal of a graph is to visually represent a set of data in a way that all of the data can be seen simultaneously processed by the interpreter. A graph is normally shown on a two-dimensional medium and thus the simplest graphs to interpret that demand the least technical training for both the presenter and the observer are also formed in two dimensions.

Some graphs can be three-dimensional, but due to the sophistication of delivering a graphing system of three dimensions on a two-dimensional portative medium, particular training is needed to create and interpret such a chart so these communications are generally not as widely spread as the much more universally involved two-dimensional graphs.

A two-dimensional graph is commonly constructed on a duo of perpendicular axes, one instructed in the vertical direction that is ordinate, the other is oriented in the horizontal direction that is abscissa, which resembles the Cartesian coordinate approach as the ‘abscissa’ and the ‘ordinate’, respectively. Where the two axes meet is directed to as the origin of a Cartesian plane.

Origin(0, 0)

The Cartesian ritual permits negative numbers to the left and the lowered side of the origin along these two axes and whole or positive values to the right and vertically upward of the origin. Therefore data from a collection of data in a table, or functional weights from mathematical formulas yield well in a Cartesian methodology.

A pictorial survey of all the data simultaneously devised on a Cartesian plane permits the viewer to detect trends, patterns, anomalies, and different data and functional elements in this production that would be less recognizable if it were introduced as a list or in table form. It is for this cause that graphs are a famous medium for depicting raw data accumulated in tables.

\[ \displaystyle (\overbrace {x} ^{\displaystyle {\text{abscissa}}},\overbrace {y} ^{\displaystyle {\text{ordinate}}}) \]

A point is a primary connection depicted on a graph. Every point is represented by a pair of numerals containing two coordinates. A coordinate is one of a bunch of numbers utilized to specify the spot of a point on a graph. Each point is determined by both an x and a y coordinate that is abscissa and ordinate respectively.

An Example of Finding the Abscissa From a Graph

Identify the number of points in the below graph and further define the abscissa and ordinate of the points.

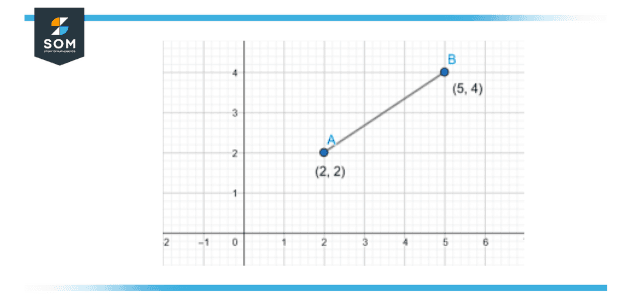
Figure 4 – Line in Cartesian Plane

Solution

In figure 3, there are two points. One is A, having coordinates (2, 2), and the second is B having the coordinates (5, 4). Point A(2, 2) has abscissa of 2 and ordinate of 2 as well, whereas point B(5, 4) has abscissa 5 and ordinate 4.

All mathematical drawings and images were created with GeoGebra.