Zero|Definition & Meaning

Zero is a numerical value representing nothing or the absence of quantity. In mathematics, it is used as a placeholder in our number system, and it has important properties in arithmetic operations, such as being additively neutral. The symbol of zero and its basic operations have been depicted in Figure 1 below: 

Figure 1: Symbol and operations on zero

Background

Around 3,000 years ago, the ancient Babylonians and Mayans created the idea of zero as a number.  The Babylonians used a symbol for zero as a placeholder in their numbering system, while the Mayans developed a sophisticated numerical system that included the concept of zero.

The Indian mathematician Brahmagupta was one of the first to give mathematical rules for the operations involving zero, such as the result of dividing by zero. The Indian mathematician and astronomer Aryabhata also made important contributions to the understanding of zero as both a placeholder and a number in its own right.

The modern representation of zero as a digit was introduced by the Arabic-speaking mathematician Al-Khwarizmi in the 9th century, who also popularized the use of the Hindu-Arabic numeral system. The Hindu-Arabic numeral system, which includes zero, quickly spread throughout the Islamic world and eventually made its way to Europe through trade and cultural exchange.

Applications of Zero

Zero has a wide range of applications in various fields, including mathematics, science, technology, and finance.

1. Mathematics: Zero is used as a placeholder in our numbering system, and it also forms the basis of the number line, allowing us to understand and compare positive and negative numbers.
2. Science: In physics, zero is used as a reference point for measuring temperature, pressure, and other physical quantities. In electrical engineering, zero volts are used as a reference voltage level.
3. Technology: Zero is used in computer programming as a null value to indicate the absence of data. It is also used in digital image processing and compression to represent the background or empty pixels.
4. Finance: Zero-coupon bonds, also known as discount bonds, are financial instruments that do not pay periodic interest but are sold at a discount and redeemed at face value. All spending for each new month must be justified when using the zero-based budgeting strategy.

In summary, zero is a crucial concept in many areas. It has many applications, from the basic operations of arithmetic to more complex fields like finance and technology.

Real-life Advantages of Zero

Zero has several practical and real-life advantages, including:

• Simplifying arithmetic operations: Zero allows us to simplify them, making it easier to perform addition, subtraction, multiplication, and division.
• Improving accuracy in measurements: In many fields, including science, engineering, and finance, zero is used as a reference point, allowing for more accurate measurements and comparisons.
• Making computations easier: Zero is a crucial component of computer programming and digital technology, making complex computations easier to perform and more efficient.
• Facilitating financial transactions: Zero is an important concept in finance, enabling transactions to be conducted with greater ease and accuracy and helping to minimize financial risks.
• Streamlining data representation: Zero is used in many digital technologies, including image processing, compression, and storage, to simplify data representation and make it easier to manage and manipulate.

One glimpse of the application of the operations of zero in real life has been shown in Figure 2 below:

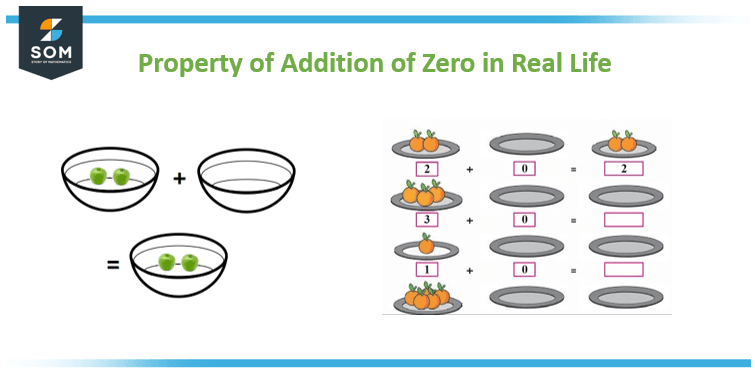
Figure 2: Real-life applications of Zero

In conclusion, zero has a multitude of practical and real-life advantages that make our lives easier, from the basic arithmetic operations we perform every day to the advanced technologies that drive our modern society.

Properties of Zero

Zero has several properties that make it unique and important in mathematics:

1. Additive identity: Zero is the additive identity, meaning that when added to any number, the result is the same number.
2. Multiplicative identity: Zero is the multiplicative identity for the set of real numbers, meaning that when multiplied by any number, the result is zero.
3. Absolute value: The absolute value of zero is zero, meaning it is neither positive nor negative.
4. Placeholder: Zero is used as a placeholder in our numbering system, allowing us to distinguish between numbers of different magnitudes.
5. Even number: Zero is an even number, meaning that it is divisible by 2 without a remainder.
6. Transitive property: Zero has the transitive property, meaning that if a + b = 0, then b + a = 0.
7. Identity for addition and multiplication: Zero is the identity for addition and multiplication, meaning that adding or multiplying zero to any number results in that number.

In summary, zero has several unique properties that make it an important and essential concept in mathematics, including its role as an additive and multiplicative identity, its significance as a placeholder, and its transitive property.

Uses of Zero in Mathematical Equations

Zero has several uses in mathematical equations, including:

Solving Linear Equations

Zero is often used as a solution to linear equations, allowing us to find the value of unknown variables.

Null Space

In linear algebra, the set of all solutions to a system of linear equations that equal zero is called the null space, which is important for understanding the behavior of linear transformations.

Identifying the Roots of Polynomials

Zero is often used to identify the roots of polynomials, which are the values of x that make the polynomial equal to zero.

Establishing the Continuity of Functions

Zero is used in calculus to establish the continuity of functions, which is a fundamental concept in mathematical analysis.

Defining Origin

Zero is used to define the origin in a coordinate system, the point at which the x and y axes intersect, and is used to plot and graph equations.

Indicating the Absence of a Quantity

Zero indicates the absence of a quantity, for example, the zero velocity of an object at rest.

Determining the Rank of Matrices

In linear algebra, zero is used to determine the rank of a matrix, which is a measure of the linearly independent rows or columns of the matrix.

In conclusion, zero has a wide range of uses in mathematical equations, from solving linear equations and determining the roots of polynomials to establishing the continuity of functions and defining the origin in a coordinate system.

Symbols and Representations of Zero

In mathematics, zero is represented by the digit “0” and can also be represented using the following symbols and notations:

1. Subscripts: In mathematical notation, zero is sometimes represented as a subscript, such as in the notation a_0 to indicate the first term of a sequence.
2. Null set: In set theory, the empty set is represented by the symbol Ø and is often referred to as the null set.
3. Null vector: In linear algebra, The null vector, denoted by the sign 0, is a vector whose members are all equal to zero.
4. Matrix with all elements equal to zero: In linear algebra, a matrix with all elements equal to zero is represented by the symbol 0_mn, where m and n stand for the matrix’s rows and columns, respectively.
5. Null function: In calculus, a function that maps all inputs to zero is called a null function and is often represented by the symbol f(x) = 0.
6. Zero vector: In linear algebra, the zero vector, denoted by the sign 0, is a vector whose members are all equal to zero.
7. Origin: The origin of a coordinate system is the intersection of the x and y axes, which is indicated by the coordinate (0,0).

Various representations of zero have been shown in Figure 3 below:

Figure 3: Various representations of zero

In conclusion, zero is represented by the digit “0” in mathematics, including subscripts, the null set, the null vector, matrices with all elements equal to zero, the null function, the zero vector, and the origin in a coordinate system, function, the zero vector, and the origin in a coordinate system.

It has also been represented by various symbols and notations throughout history, including the Indian dot, the Arabic digit “0”, the Roman absence of symbols, subscripts, and the null value.

Examples Involving the Concept of Zero

Example 1

Solve the equation x + 2 = 2.

Solution

To solve this equation, we need to isolate the variable x by subtracting 2 from both sides:

x + 2 – 2 = 2 – 2

x = 0

So, the solution to the equation is x = 0.

Example 2

Solve the equation 3x – 6 = 0.

Solution

By taking variable x by adding 6 to both sides and dividing both sides by 3:

3x – 6 + 6 = 0 + 6

3x = 6

(3x) / 3 = 6 / 3

x = 2

So, the solution to the equation is x = 2.

Example 3

Solve the equation 5y = 0.

Solution

We need to isolate the variable y by dividing both sides by 5:

5y / 5 = 0 / 5

y = 0

So, the solution to the equation is y = 0.

In all examples, zero is used as a solution to the equation, helping us find the value of the unknown variable x or y.

All images/mathematical drawings were created with GeoGebra.

Yard Definition < Glossary Index > Abscissa Definition