JUMP TO TOPIC
Yard|Definition & Meaning
Definition
Yard, denoted by yd, is the unit of length that equals 3 feet (36 inches) or 0.9144 meters. Equivalently, a distance of 1 mile equals 1760 yards.
Usually, the yard is a part of the imperial system that the United States still adopts to express distance units in feet, inches, and yards.
Furthermore, other imperial units, such as pounds, miles, etc., are also used to indicate their respective quantities.
The yard is frequently used to measure distances in sports and other physical activities, as well as in construction and real estate.
In the textile business, it is also used to measure the length of cloth or other materials. The term yard is also used in nautical measures. It is the unit of length used to measure the length of a ship or the depth of water in a harbor or channel in this context.

Figure 1: Conversion of Yard to meters and centimeters in SI Units
Furthermore, yards are frequently used in landscaping to gauge the size of lawns, gardens, and other outdoor spaces. For instance, a landscaper may use yards to calculate how much sod is required to cover a certain patch of lawn or how much mulch or other materials are required to cover a garden bed. Yards may also determine a property’s size and how the landscaping will be laid out.
Imperial System and Its Usage
The Imperial system, often known as the British system or imperial units, is a measuring system that was widely used in the United Kingdom and its former colonies, including the United States. The Imperial system contains the length (inches, feet, yards, and miles), weight (ounces, pounds, and tonnes), and volume units (fluid ounces, pints, quarts, and gallons).
Furthermore, Temperature (Fahrenheit), energy (British thermal units), and pressure are also included in the Imperial system (pounds per square inch). Although used widely before, nowadays, the metric system is used instead throughout most of the globe, including the United States.
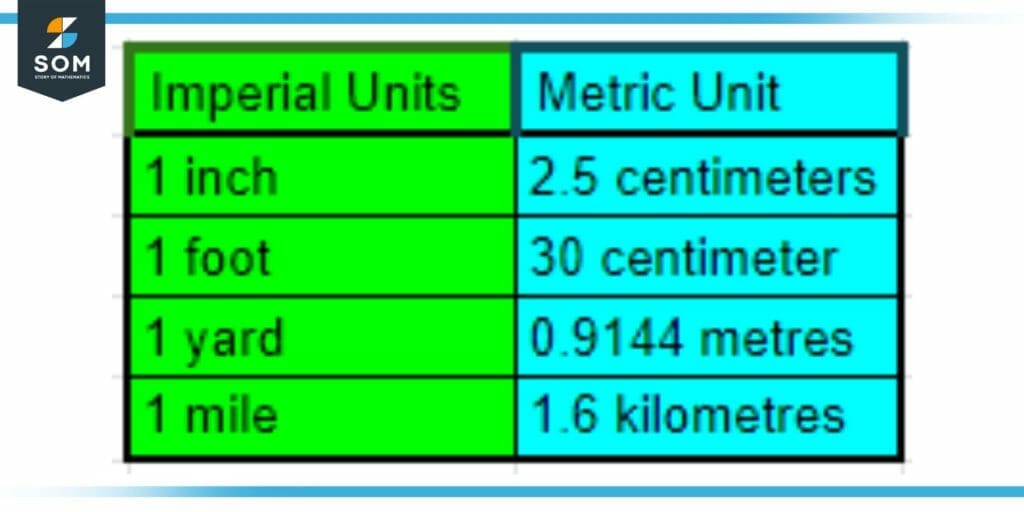
Figure 2: Imperial Units and their equivalent in SI Units.
The Imperial System was first established in the United Kingdom in the 18th and 19th centuries and was standardized in its colonies, such as the United States. It was widely used throughout the 19th and 20th centuries but later on, lost its usage at the end of the 20th century.
The usage of scientific improvements and occurrences of technological advances changed the whole retrospective around the quantities and their measurement, and thus, the metric system was considered to be a more logical and consistent system of measurement of units. Thus, the world shifted to the SI Unit system.
Nowadays, the SI Unit is the mainstream way of measurement of quantities. However, the imperial system is still widely used in measurements in everyday life, such as road distances, body temperatures, cooking quantities, and industries.
Importance and Uses of Yard in Practical Applications
The yard is a pretty commonly used unit of measurement of distance in the US, and many landscaping or distances are related to sports, real estate, textile and clothing, and food and agriculture. Furthermore, It is also an important tool of measurement for construction works, with the dimensions of the rooms and lots measured in yards and feet.
Similar to how the size of a house or the area of a plot of land can be described, the yard is frequently employed in real estate. Because of this, it is simple for purchasers to comprehend a property’s dimensions.
The unit yard is used in landscaping to determine the size of lawns and gardens as well as the number of materials required for projects. This enables both experts and individuals to plan and carry out landscaping tasks precisely.
The yard is also used in the textile and apparel industries to measure materials or clothing and ensure that garment measurements are precise.
Moreover, yards are a common unit of measurement in sports for field or track events like the long jump and the 100-yard race. This makes it possible to quantify sports performance precisely and consistently.
Additionally, these are also used in agriculture and fishing to measure the length of a fishing net or the size of an agricultural plot. This enables precise yield computation and resource management.
Examples Explaining the Usage of Yard and Imperial System in Measurements
Example 1
A property dealer bought land for \$0.5 Per Yard2. The land was 25 meters long and 50 meters wide. Find the area of the land in the unit, yard, and, subsequently, the cost of the land that the property dealer has bought.
Solution
First of all, we require to convert the metric units into imperial units, that is, meters to yards.
To convert meters to yards, we follow the following conversion:
1 metre = 1.09361 yards
25 meters = (1.09361 x 25) yards
25 meters = 27.34 yard
50 meters = (1.09361 x 50) yards
50 meters = 54.681 yards
So the land is 27.34 yards long and 54.681 yards wide.
Thus the area of the land is equal to the following:
Area of land = 54.681 x 27.34
Area of land = 1494.98 yard2
Thus the Area that the property dealer bought was 1494.98 sq yards, and its cost can be calculated as below:
Cost of land = 0.5 USD/sq yard x 1494.98 sq yards
Cost of land = 747.5 USD.
Hence, the cost of the land for the property dealer is \$747.5.
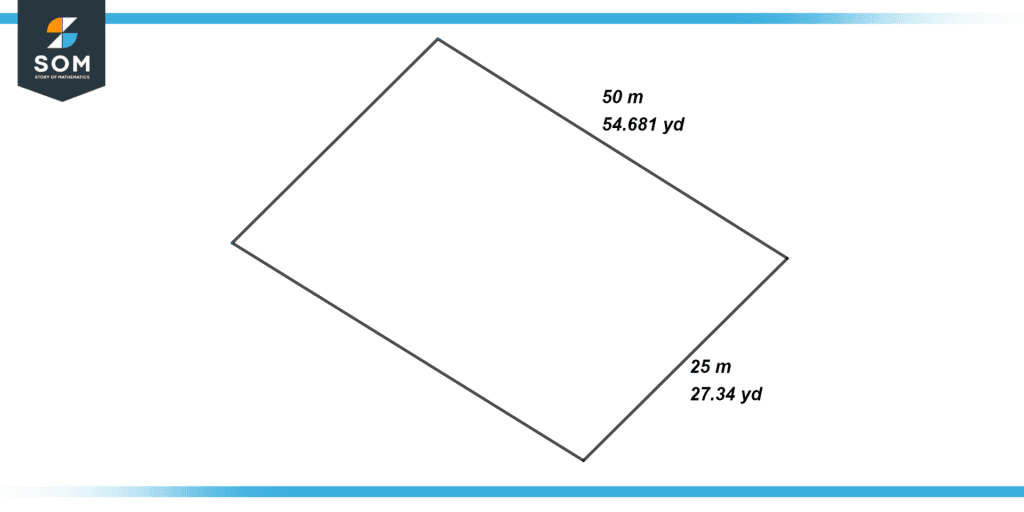
Figure 3: Illustration showing the parameters of the land bought by the property dealer
Example 2
A salesman is selling linen for \$25/yard to a clothing shop. The dealer of the clothing shop buys 10 meters of linen from the salesman. Find the cost of the linen for the dealer.
Solution
Similarly to Example 1, we have to convert the metric units to imperial units.
Length of Linen bought = 10 meters x 1.09361 yards
Length of Linen bought = 10.9361 yards
Now, the cost of linen can be calculated by the following steps:
Cost of Linen = 10.9361 yards x \$25/Yard
Cost of Linen = \$273.4025
Hence, the final cost of linen bought by the dealer is \$273.4025.
All the above figures are drawn using GeoGebra.
