JUMP TO TOPIC
Y Coordinate|Definition & Meaning
Definition
On a Cartesian graph, the y-coordinate (also called the ordinate) of a point represents how far along the y-axis it lies. Usually, the y-axis points straight up and down, so it tells us about the vertical position of the point. Since we write point coordinates as ordered pairs of the form (x, y), the second coordinate is always the y-coordinate.
Demonstration and Explanation
A y-coordinate is the 2nd value in an ordered pair, which is the combination of the x and y values of a point in a graph. We use these points to help us locate the origin and find the distance. So a y coordinate will tell us about the vertical distance from the origin. For example:
A = ( 1, 4 )
Here the number 4 represents the y coordinate on a plane. This shows that the origin is 4 points below the number 4 on a 2D plane.
When representing a y coordinate on a plane, we must first understand the position of points on a cartesian plane concerning the mathematical signs.
The Coordinates are used to divide the cartesian plane into 4 quadrants using axes XX’ and YY’. Following are the 4 quadrants:
- The region XOY is called the 1st quadrant; here, both X and Y are positive.
- The region X’OY is called the 2nd quadrant; here, only X is positive and Y is negative.
- The region X’OY’ is called the 3rd quadrant; here, X is negative and Y is positive.
- The region Y’OX is called the 4th quadrant; here, both X and Y are negative.
When representing these in a plane, we can see the following example:
A = ( 2, 6)
B = ( 4, 8)
C = (6, 2)
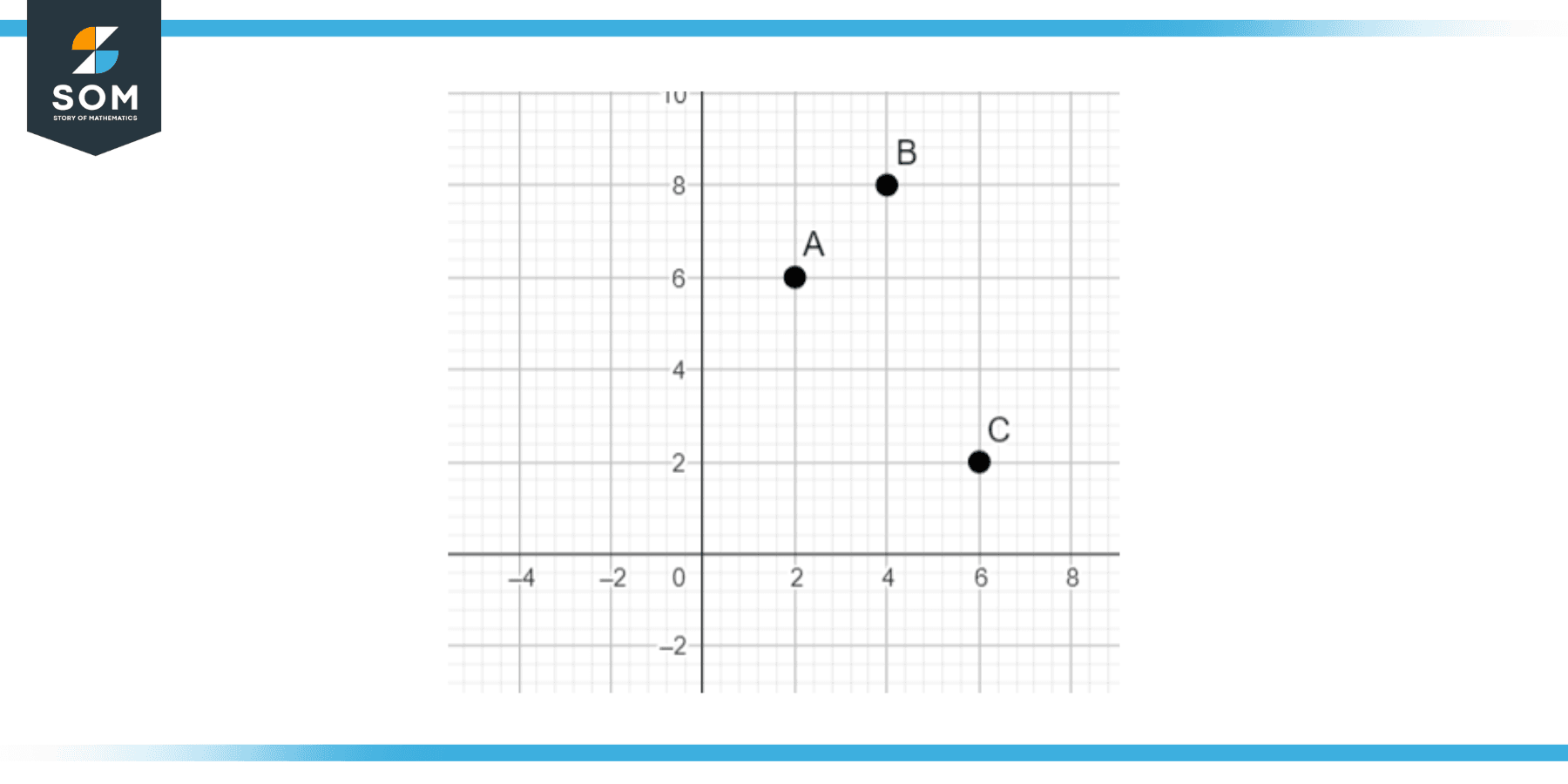
Figure 1 – 3 points representing Y coordinates
Here we can see that the plotting has been done by using both coordinates representing the distance of the points from their origin.
Now, look at the following example, which describes the importance of quadrants and y coordinates.
A = ( -6, 4)
B = (6, -4)
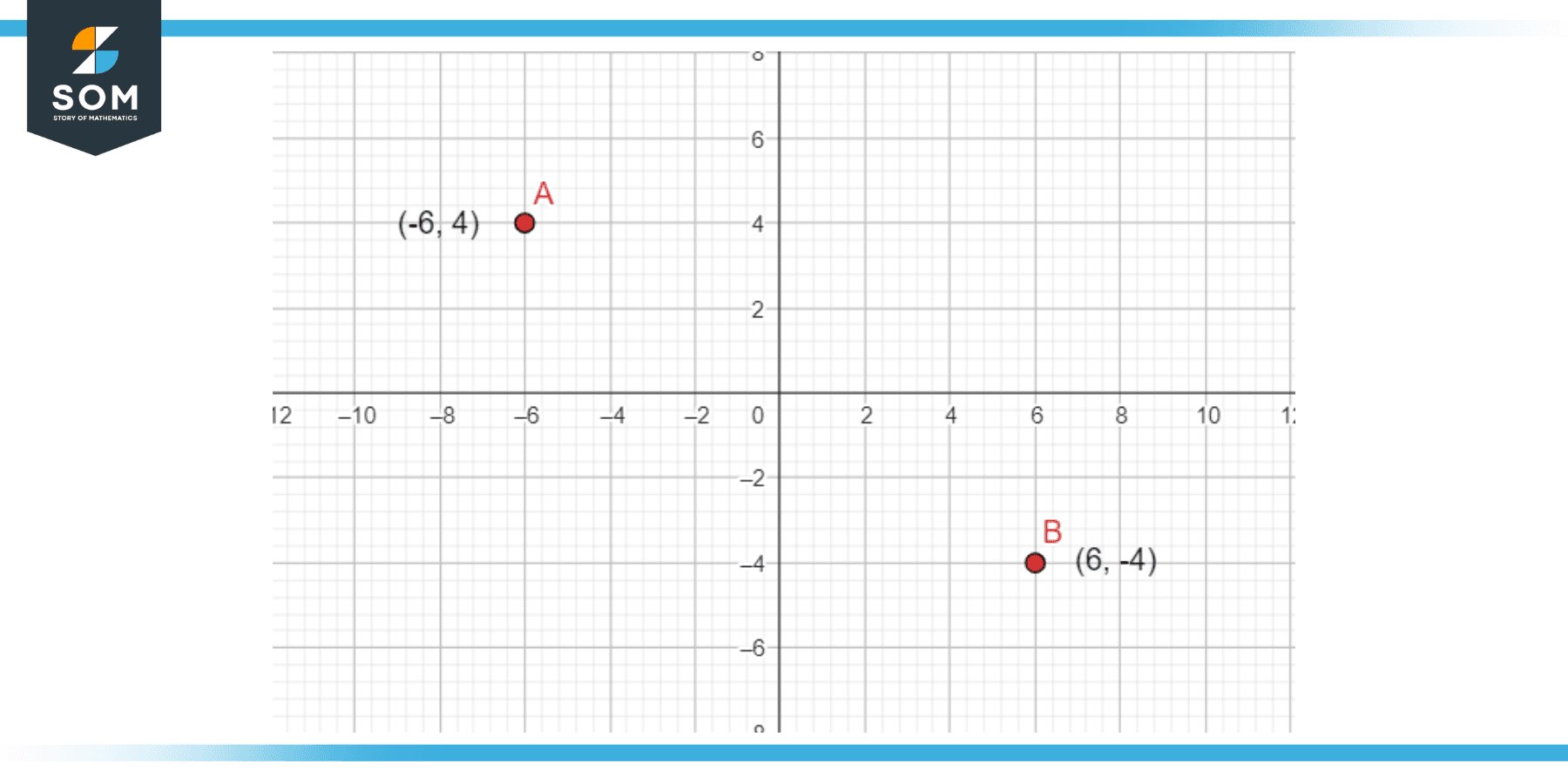
Figure 2 – Positive and Negative representation of Y coordinate
In this image, we can see that the change in the signs of the y coordinate from positive to negative can completely alter the position of the point from its origin.
Relation Between X and Y Coordinate
The relation between both the coordinates X and Y are directly proportional. This is because if we want to find one of these, say x. We can always use the other, say y, to find it. We can describe the relationship by using the following rule that states; when 2 is added in the values x coordinate, then it is equal to the y coordinate. Hence the equation that we can use is:
X + 2 = Y
| X coordinate | Solving X + 2 = Y | Y coordinate | Ordered pair |
| 1 | 1 + 2 = 3 | 3 | (1, 3) |
| 2 | 2 + 2 = 4 | 4 | (2, 4) |
| 3 | 3 + 2 = 5 | 5 | (3, 5) |
| 4 | 4 + 2 = 6 | 6 | (4, 6) |
| 5 | 5 + 2 = 7 | 7 | (5, 7) |
To form the linear relation between these ordered pairs, we will first plot them and later will connect them to verify that the equation is true. Let:
A = (1, 3)
B = (2, 4)
C = (3, 5)
D = (4, 6)
E = (5, 7)
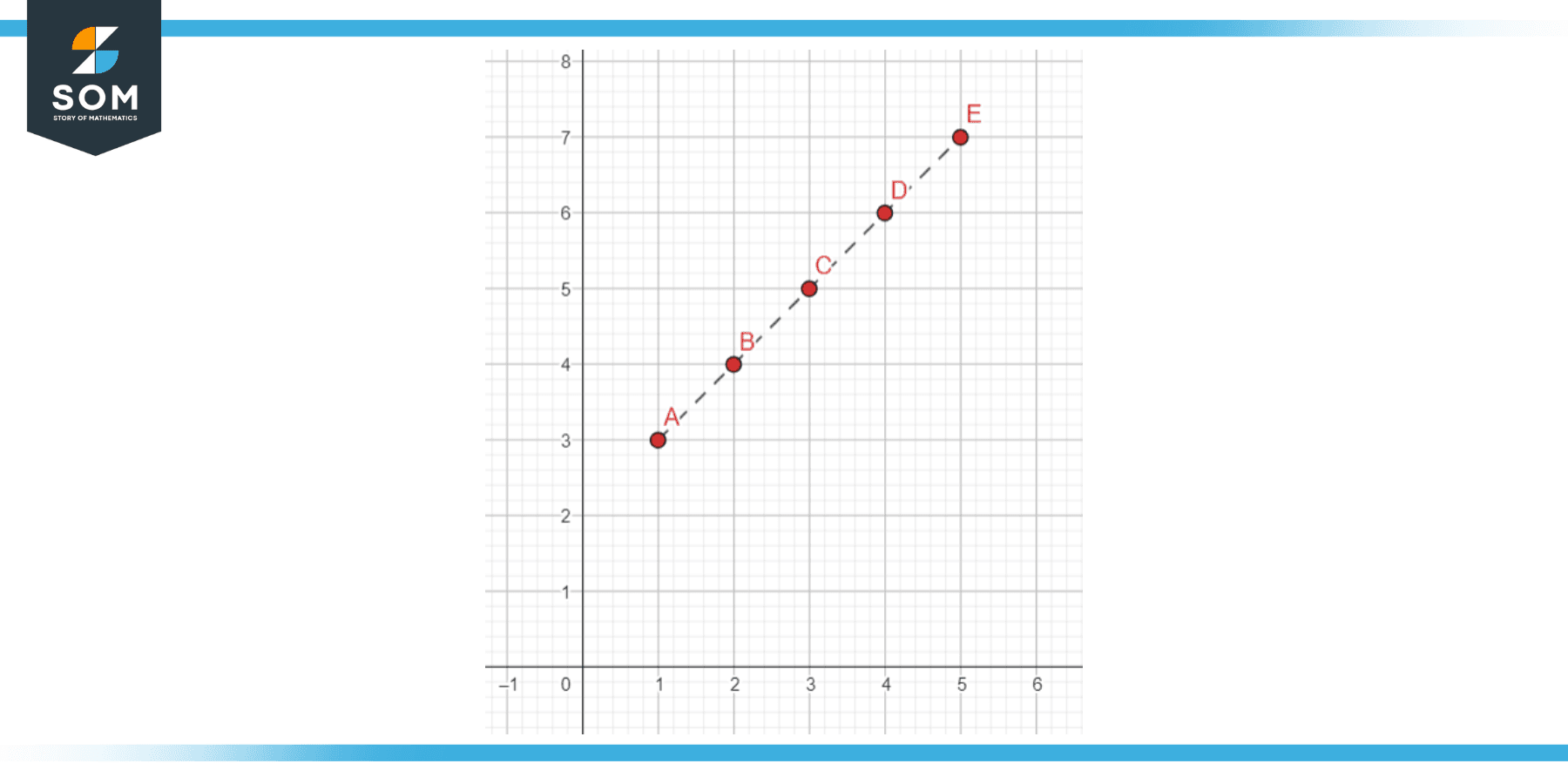
Figure 3 – Linear relation between X and Y coordinate
Here we have plotted the coordinates and have connected the points, which are in the form of a straight line which confirms the linear relation between x and y coordinates.
Measuring the Verticle Distance
To measure the length of a vertical line segment, we take the absolute value of the endpoints after taking the difference of the y coordinates. Let us take a look at the following example for a better understanding of these concepts.
A = (5, 4)
B = (5, -2)
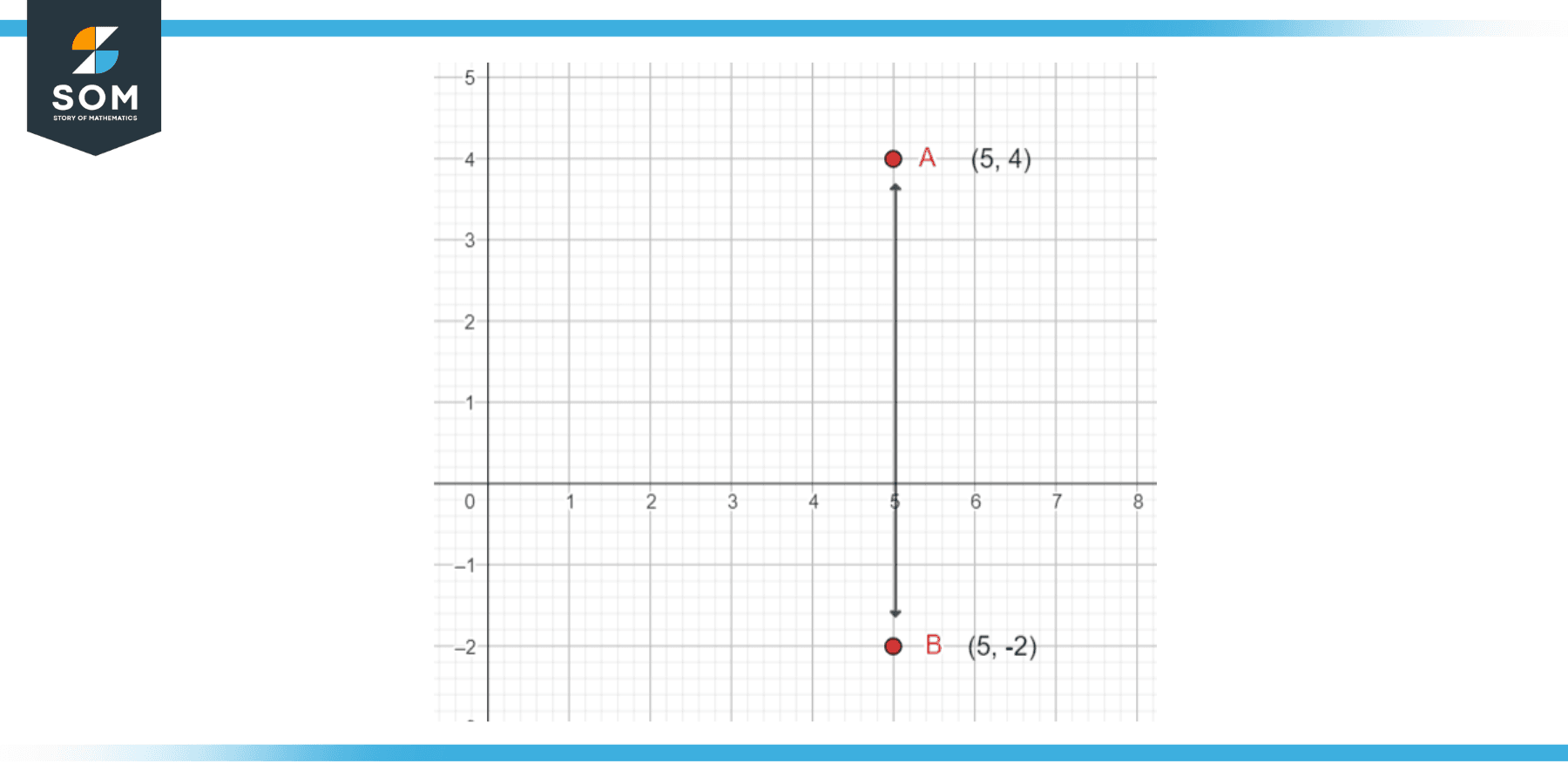
Figure 4 – Vertical distance of Y coordinate
We can count the units along the y-axis from 1 endpoint to another to determine the length of the line, or we can take the absolute value and the difference between those values:
|4 – (-2)| = |6| = 6 units
Or:
|-4 -2| = |-6| = 6 units
We tend to use this method, particularly for larger distances, so that we don’t have to count so many of the units, and there might be a difference in scales.
Uses of Y Coordinate
- We use the y coordinate to find the vertical distance of points.
- Y coordinate helps us to find the origin vertically.
- We can find the slop of a line with the help of x and y coordinates.
- We use the y coordinate to find the distance of a point from its origin.
Examples Involving Y Coordinates
Example 1
Help Juniper to find the x and y coordinates of the midpoint of a ribbon by joining the points (2, -3) and (1, 4).
Solution
The given points of the ribbon are (x1, y1) = (2, -3), and (x2, y2) = (1, 4)
Using the midpoint formula:
Mid Point = [ (x1 + x2)/2, (y1 + y2)/2 ]
Now putting values in the formula, we get:
= [ (2 + 1) / 2, (-3 + 4) / 2 ]
= (3/2, 1/2)
= (1.5, 0.5)
Example 2
What is the other name of the y coordinate?
Solution
The y coordinates are also referred to as ordinate, just like the x coordinates are known as abscissa. This term is not used that much now, but the ordinate refers to the vertical distance of points concerning the origin. If the origin is below the ordinate, then it is positive, and when the origin is above the ordinate, then it is negative.
Example 3
Find the vertical distance of the following:
A = (8, -3)
B = (0, 2)
C = (3, 7)
D = (2, -2)
Solution
To find the vertical distance, we will take the difference of the y coordinates and take the absolute value to determine the number of units.
|-3 – 2| = |-5| = 5 units
|7 – (-2)| = |9| = 9 units
Since we are finding the vertical distance only so we will ignore the values of the x-axis.
Example 4
Find the quadrant of the following based on their y-coordinate:
A = (2, 6)
B = (2, -6)
Solution
If we look at A, then both the x and y coordinates are positive, so it means that it is in the 1st quadrant, whereas B has a positive x coordinate and a negative y coordinate which shows that it is from the 2nd quadrant.
Images/mathematical drawings are created with GeoGebra.
