JUMP TO TOPIC
Arm Of An Angle|Definition & Meaning
Definition
The arms of an angle can be defined as two lines that join each other at a common intersection to form an angle. The common intersection is known as a vertex. One of the arms is usually stationary while the other one moves around to form the angle.
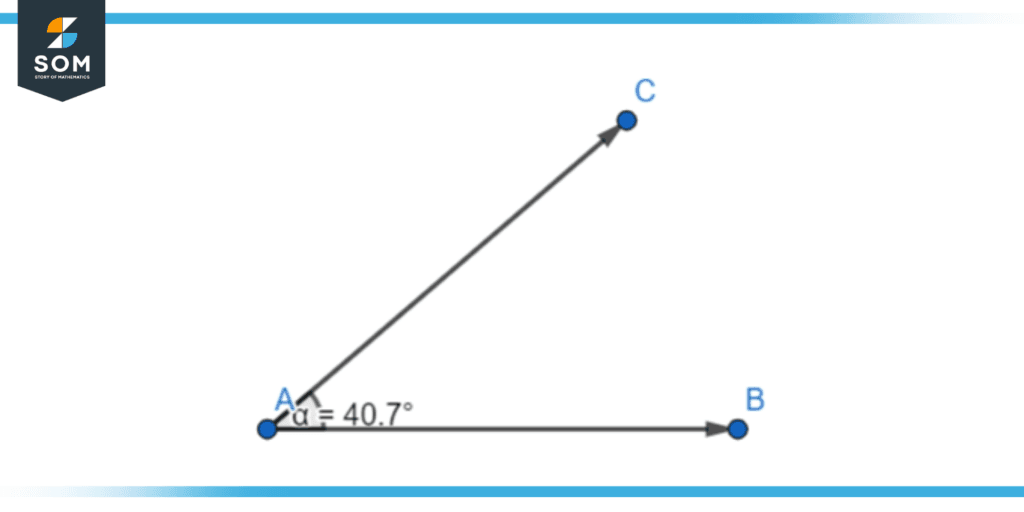
Figure 1 – The arms of this angle are the rays AB and AC.
The two arms of the angle define the degree of rotation of the angle. One of the arms remains at a fixed point at the axis and does not move, it is known as the stationary arm. The second arm is free to move and rotates around the stationary arm around a fixed axis. The vertex is the point where both arms meet to form the angle.
The stationary arm usually remains at the x-axis. If both arms are on this axis, then the angle, by convention, is considered zero. From this understanding, there can be two types of movements that the stationary arm can make. It can either revolve in a clockwise direction or an anti-clockwise direction.
By convention, the anticlockwise or counter-clockwise movement is taken as a positive movement, whereas the clockwise movement is taken as a negative movement.
Counter-clockwise and Clockwise Movement of the Arms
As mentioned earlier, the rotating arm can move in two directions:
- Clockwise Rotation
- Anti-clockwise or Counter-clockwise Rotation
Some conventions need to be followed to define the difference between the arm moving in either direction. One convention can be standardized for understanding the concept of positive and negative angles.
By convention, when the stationary arm is on the x-axis and the movement of the rotating arm is in the clockwise direction, the rotation is considered to be the negative rotation and the angle thus formed by the vertex of these arms is also taken as negative.
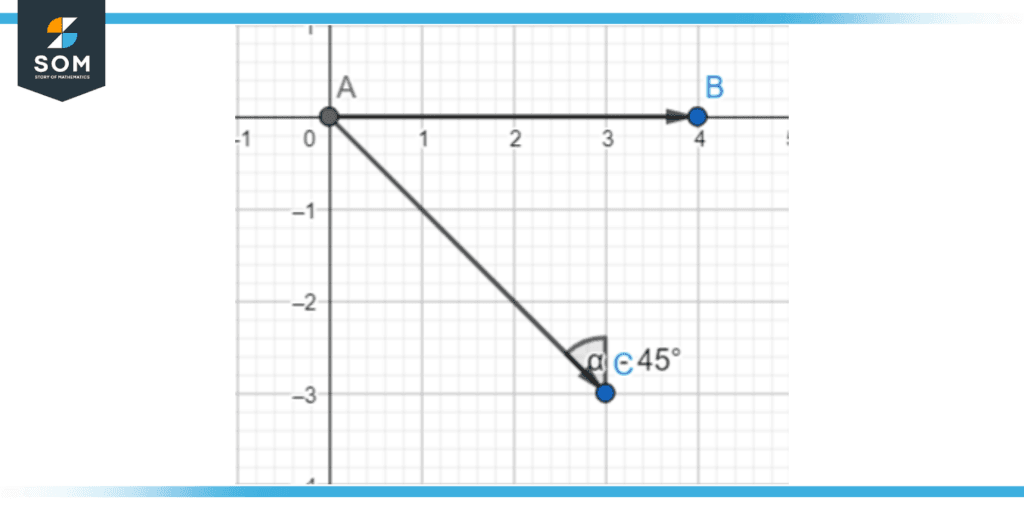
Figure 2 – The arm AC has rotated 45 degrees clockwise from the arm AB.
By convention, when the stationary arm is on the x-axis and the movement of the rotating arm is in the anti-clockwise direction, the rotation is considered to be the positive rotation and the angle thus formed by the vertex of these arms is also taken as positive.
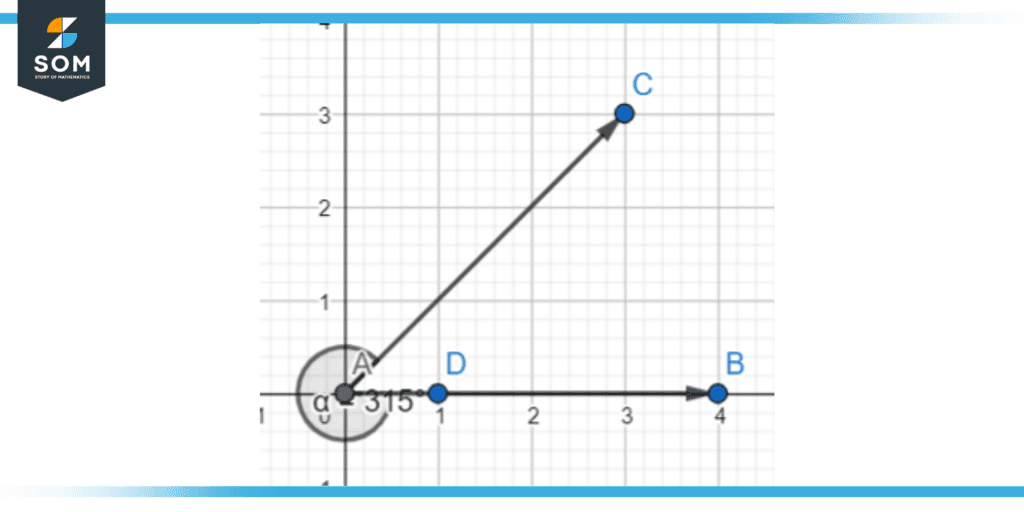
Figure 3 – The arm AC has rotated 45 degrees anti-clockwise from AB, or equally 315 degrees clockwise.
A Deeper Explanation of the Arms of an Angle
There are three basic components of an angle that need to be understood:
- Stationary Arm
- Rotating Arm
- Vertex
The stationary arm remains at the x-axis. This is the arm of reference. We can compare the rotating arm to this arm to define the difference in their position.
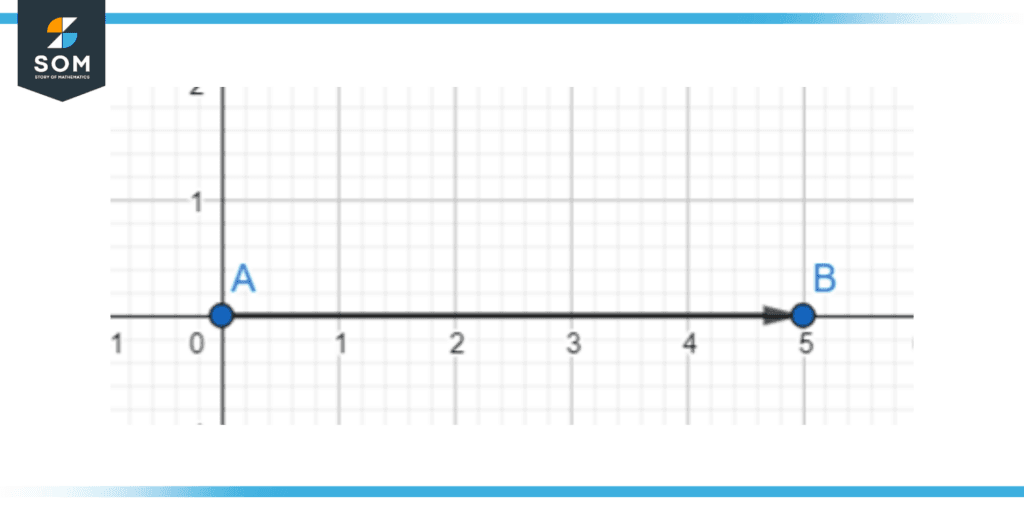
Figure 4 – A stationary arm (or ray) along the x-axis.
The rotating arm is the arm that is responsible for determining the angle that is formed between it and the stationary arm. It can move freely on either side of the stationary arm, either moving clockwise or counter-clockwise.
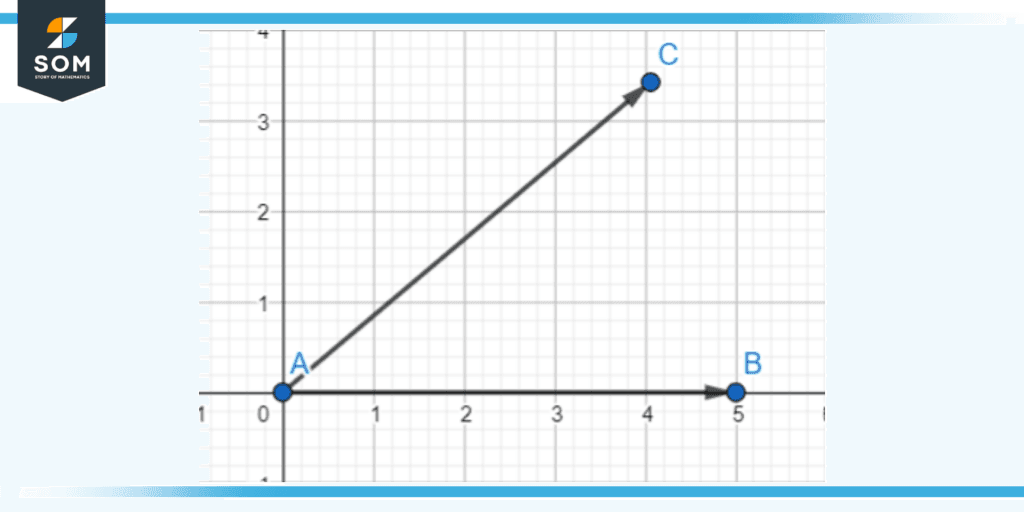
Figure 5 – The ray AB can rotate a certain amount and end up as the ray AC, forming an angle between AB and AC.
The vertex is the meeting or joining common point of the stationary and rotating arms. It defines the angle. It can either produce a negative or positive angle depending upon the rotation of the rotating arm around the stationary arm.
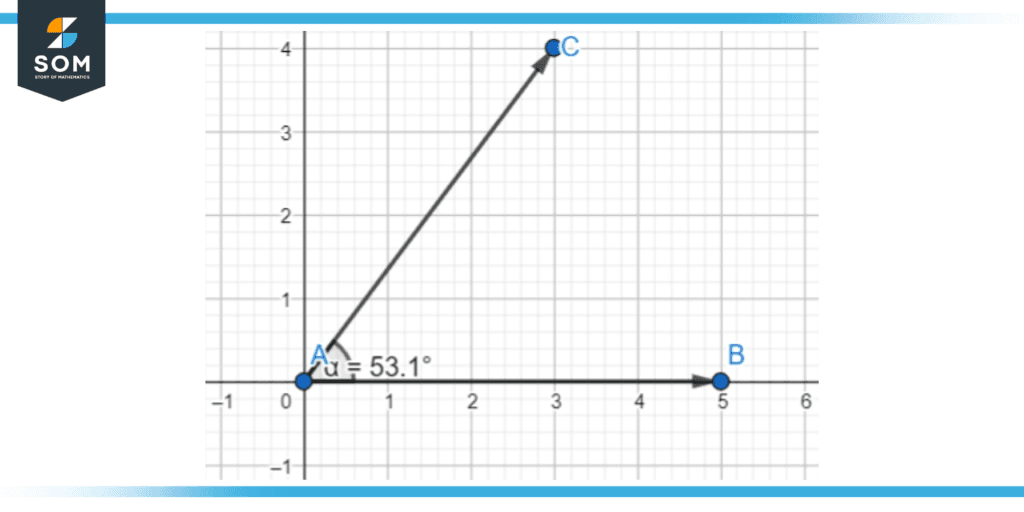
Figure 6 – The vertex A joins the two arms together. Measuring the angle between them, we get 53.1 degrees.
The System of Quadrants
The arms lie in the 4 Quadrants System. If the rotating arm moved in either direction starting from the starting position x=0, it would cover a total of 360°, thus making a complete rotation after reaching back to zero from either side (One can be taken as a reference).
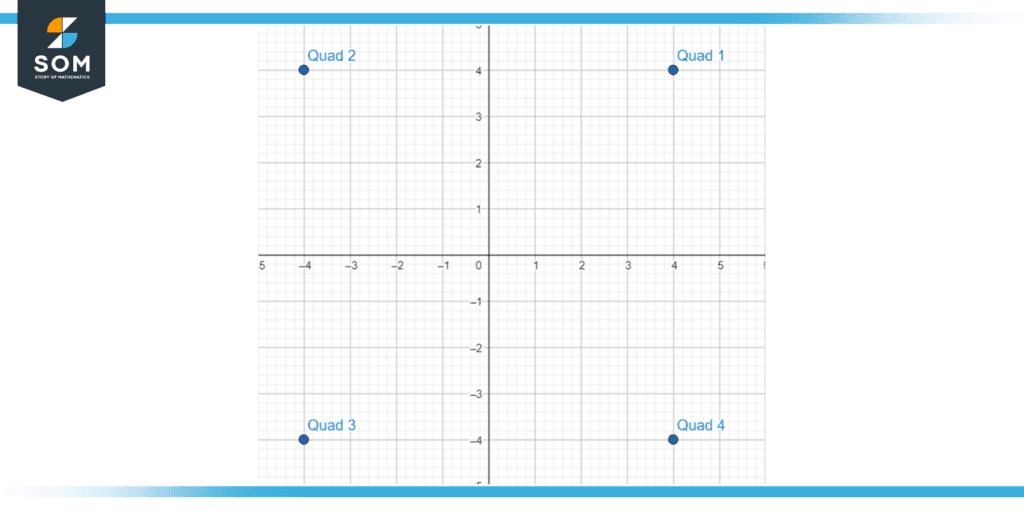
Figure 7 – The 2D Cartesian coordinate quadrant system.
If we move with the convention that anti-clockwise rotation is positive, the angle in the first quadrant will be from 0° to +90°. It will be a positive movement and the coordinates of the rotating arm would be (x,y).
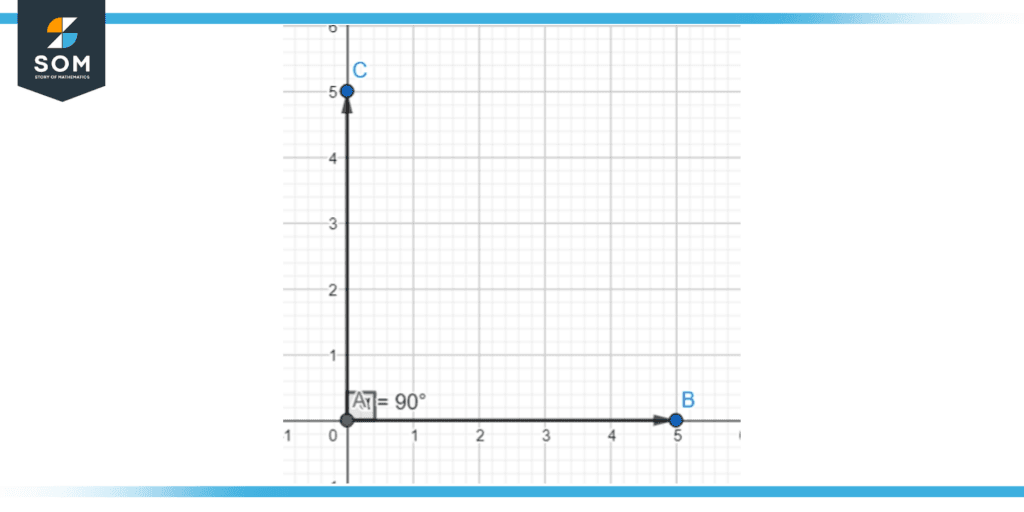
Figure 8 – The first quadrant lies between the angles of 0 and 90 degrees.
If we move in the anti-clockwise position further, the angle in the second quadrant will be from 0° to +180°. It will still be a positive movement by convention and the coordinates of the rotating arm would be (-x,y).
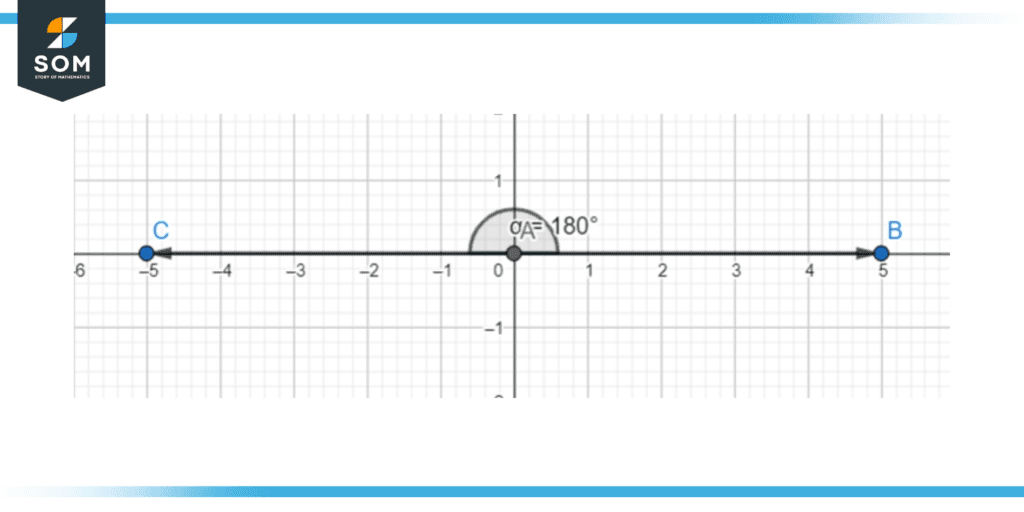
Figure 9 – The second quadrant starts at 90 degrees and ends at 180 degrees.
If we move in the anti-clockwise position further, the angle in the third quadrant will be from 0° to +270°. It will still be a positive movement by convention and the coordinates of the rotating arm would be (-x,-y).
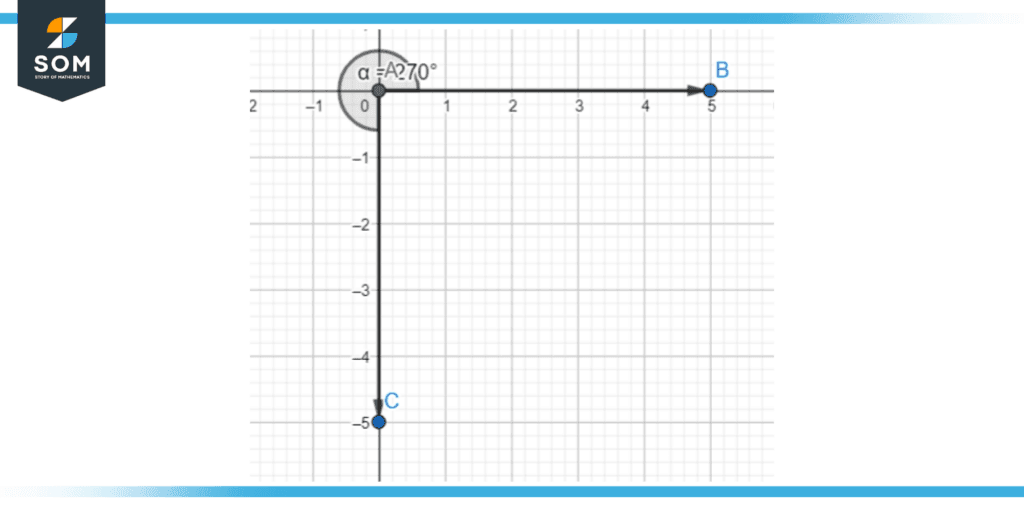
Figure 10 – The third quadrant lies between the angles of 180 and 270 degrees.
If we move in the anti-clockwise position even further to complete a rotation, the angle in the fourth quadrant will be from 0° to +360°. It will still be a positive movement by convention and the coordinates of the rotating arm would be (x,-y).
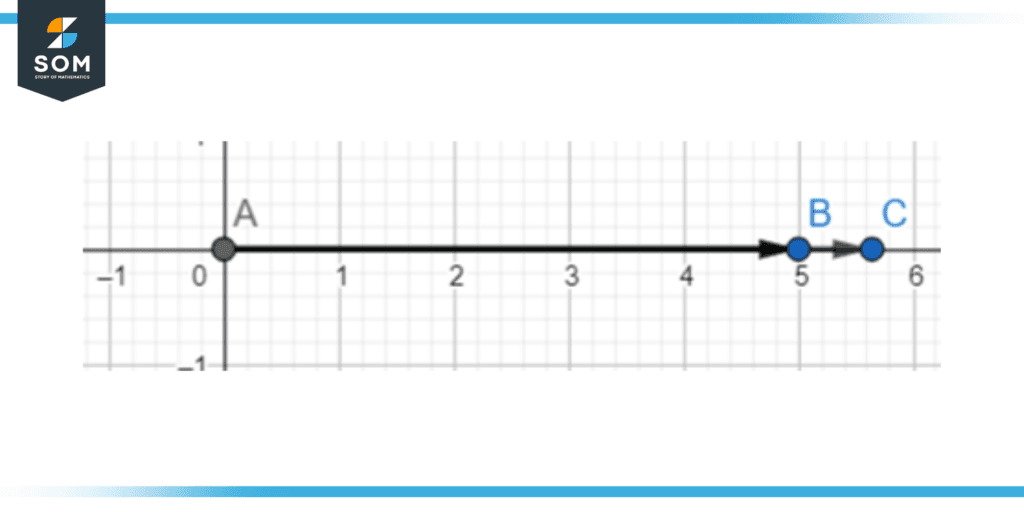
Figure 11 – The fourth quadrant exists between 270 and 360 degrees, and coincides with the boundary of the first one.
The angles would be negative with this convention if the stationary arm moves in the clockwise direction. it would be a -360 for a complete clockwise rotation.
Illustrations of Arms of an Angle With Some Unique Angles
As we have discussed that the rotating arm of the angle can be revolved around the quadrant system to get a complete rotation and the complete is divided into 360 Degrees (From 0° to 360°). There is specific and unique nomenclature for the angles formed along the quadrant system.
Acute Angle
When the rotating arm lies in the first quadrant, the angle can range from 0° to 90°. Any angle between 0° to 90° is known as the acute angle. It is represented as:
Acute angle = 90° > α > 0°
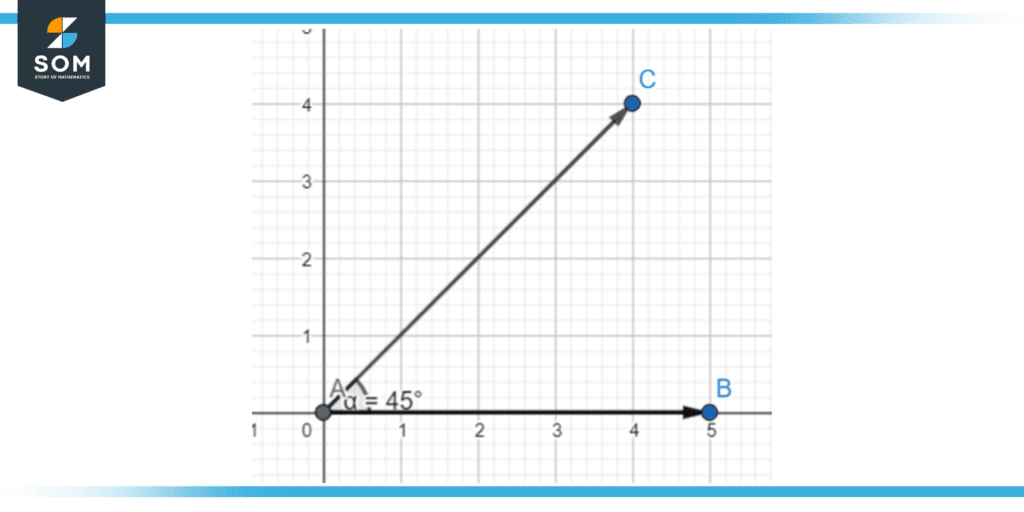
Figure 12 – An acute angle of 45 degrees (first quadrant).
Right Angle
When the rotating arm lies on the edge of the first and second quadrants, the angle can range from 0° to 90°. Any angle that is exactly 90° is known as the right angle. It is represented as:
Right angle = α = 90°
Figure 8 represents a right angle.
Obtuse Angle
When the rotating arm lies in the second quadrant, the angle can range from 90° to 180°. Any angle between 90° to 180° is known as the obtuse angle. It is represented as:
Obtuse angle = 180° > α > 90°
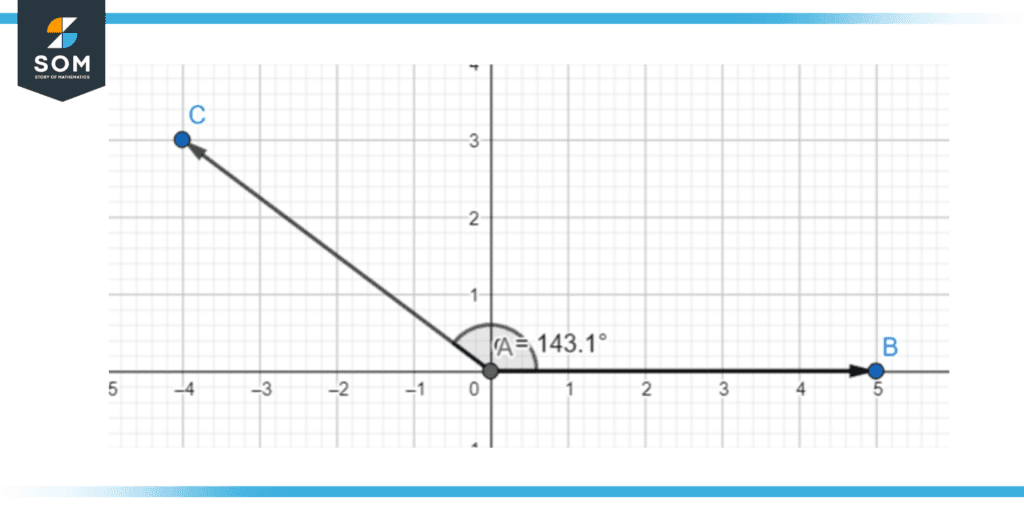
Figure 13 – An obtuse angle of 143.1 degrees (second quadrant).
Straight Angle
When the rotating arm lies on the edge of the second and third quadrants, the angle can range from 90° to 180°. Any angle that is exactly 180° is known as a straight angle. It is represented as:
Straight angle = α = 180°
Figure 9 represents a straight angle.
Reflex Angle
When the rotating arm lies in the third quadrant, the angle can range from 180° to 270°. Any angle between 180° to 270° is known as the obtuse angle. It is represented as:
Reflex angle = 270° > α > 180°
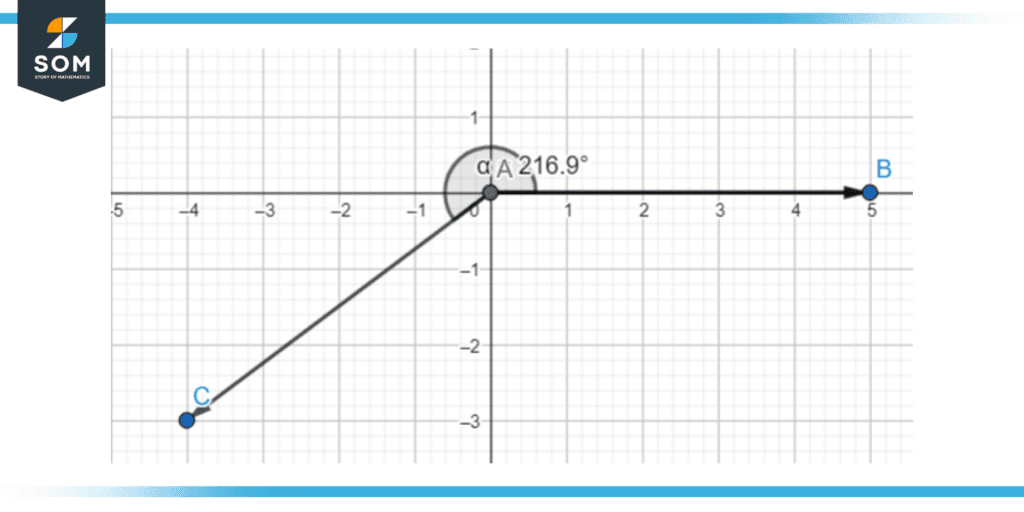
Figure 14 – A reflex angle of 216.9 degrees (part of the third quadrant).
Understanding Arms of an Angle With Examples
Consider the following angles:
- 87°
- 99°
- 267°
- 360°
- 180°
- 90°
Kindly please identify each of the following angles based on their uniqueness.
Solution
1) 87°
As we can see that this angle lies in the first quadrant and follows the relation: 90° > α > 0°, we can easily identify it as an acute angle.
2) 99°
As we can see that this angle lies in the second quadrant and follows the relation: 180° > α > 90°, we can easily identify it as an obtuse angle.
3) 267°
As we can see that this angle lies in the third quadrant and follows the relation: 270° > α > 180°, we can easily identify it as a reflex angle.
4) 360°
As we can see that this angle lies in the fourth quadrant and has completed a full rotation, we can easily identify it as a complete angle or a complete revolution.
5) 180°
As we can see that this angle lies on the edge of the second and third quadrants and has completed a half rotation, we can easily identify it as a straight angle or a half revolution.
6) 90°
As we can see that this angle lies on the edge of the first and second quadrants and has completed a quarter of a rotation, we can easily identify it as a right angle.
All images used in this article were made with GeoGebra.
