Classify|Definition & Meaning

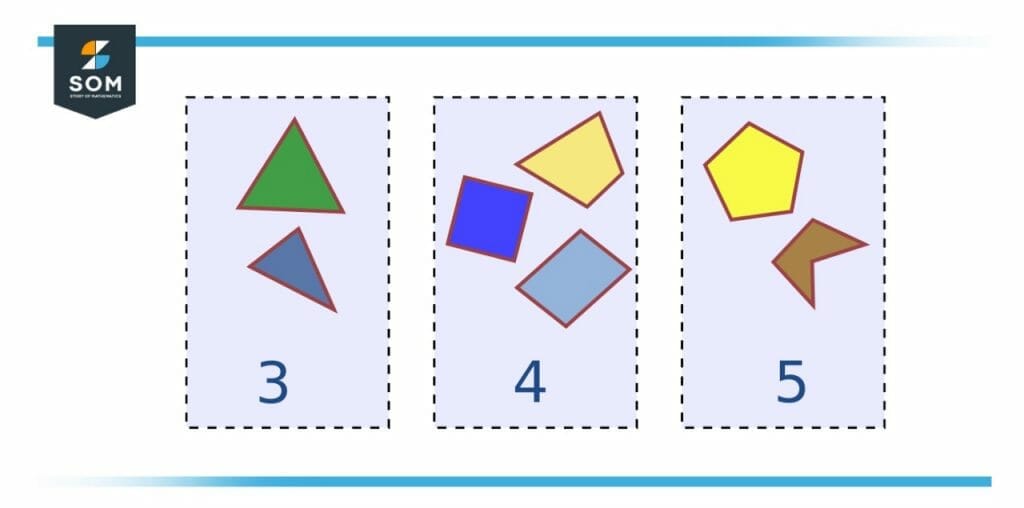
Figure 1 – Definition of the Concept of Classify

The process of classification can help to simplify and organize information and can also aid in problem-solving and decision-making. 

What Are the Important Points of Classify in Mathematics?

In mathematics, classification is an important tool for organizing information and simplifying problem-solving. Some key points related to classification in mathematics include:

1. Identifying characteristics or properties: In order to classify mathematical objects, it is important to be able to identify and define the characteristics or properties that will be used to group them into categories.
2. Categorizing based on shared properties: The process of classification involves grouping mathematical objects together based on shared characteristics or properties. This can help to simplify and organize information, making it easier to understand and work with.
3. Using classification to solve problems: Classifying mathematical objects can aid in solving problems and making generalizations. For example, classifying geometric shapes by their number of sides can help to make predictions about how those shapes will behave in certain situations.
4. Classifying numbers: Numbers can be classified into different types, for example, natural numbers, integers, rational numbers, irrational numbers, and real numbers. Understanding the classification of numbers is important for solving mathematical problems and understanding mathematical concepts.
5. Classifying functions: Function classification is used to group functions with similar properties or behavior together. It is a useful tool for understanding and analyzing functions.
6. Machine Learning: In Machine Learning, classification is a way to build models that can predict the class/category of a given input. This can be used in many applications, such as image recognition, speech recognition, and natural language processing.

What Does It Mean To Classify Numbers?

Classifying numbers refers to the process of grouping numbers based on their properties or characteristics, such as their type, value, or behavior. Common types of numbers that are classified in mathematics include natural numbers, integers, rational numbers, irrational numbers, and real numbers. 

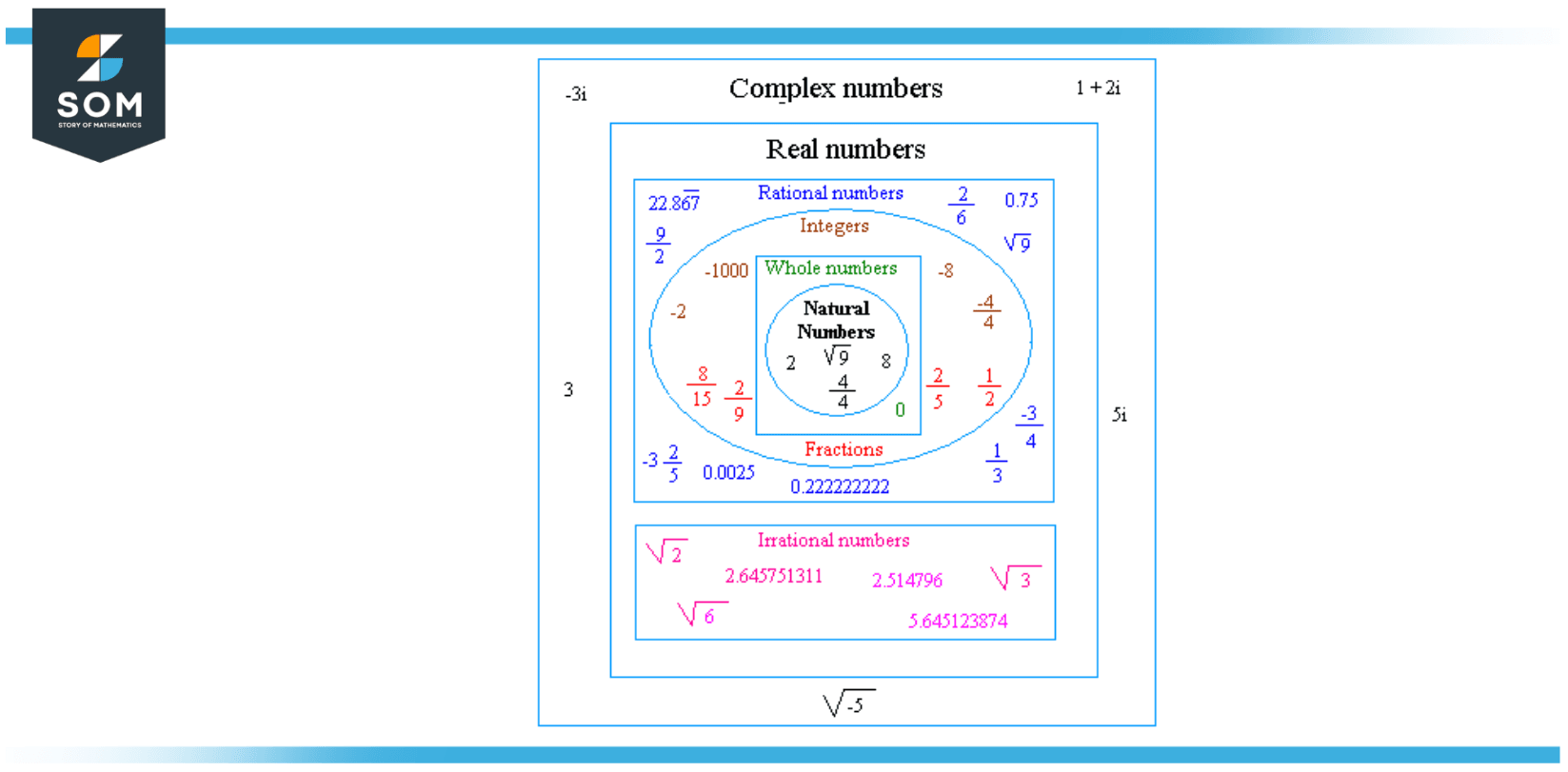
Figure 2 – Classification of numbers as complex and real.

Each of these groups of numbers has different characteristics and is used in different areas of mathematics. Understanding the classification of numbers is important for solving mathematical problems and understanding mathematical concepts.

What Are Classifying Functions?

Classifying functions refers to the process of grouping functions with similar properties or behavior together. This can be done based on the function’s type, domain, range, or other characteristics.

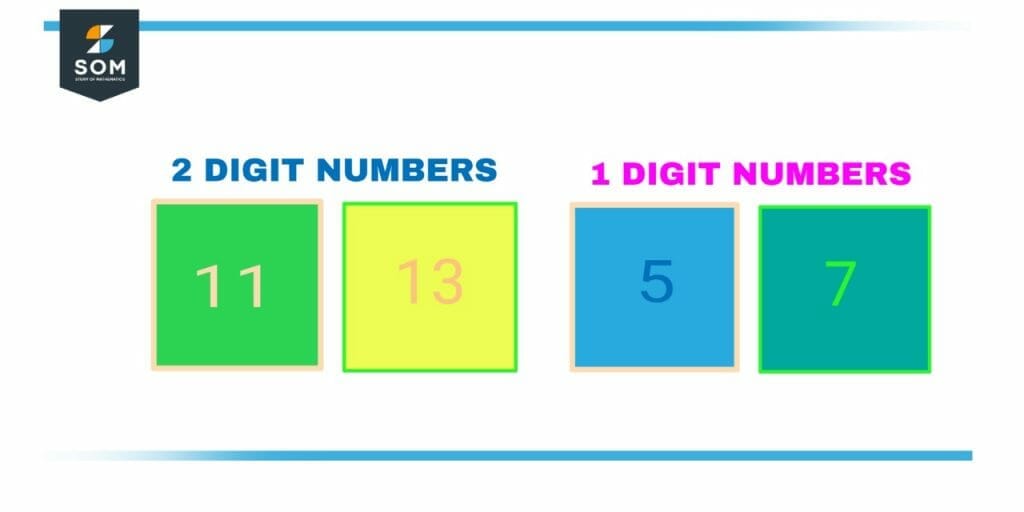
Figure 3 – Separate 1-digit numbers and 2-digit numbers classification functions

What Are Classify Types?

There are many ways to classify things, depending on the context and the information being considered. Here are a few examples of common classifications types:

1. Categorical: This type of classification involves grouping items into categories based on shared traits or characteristics. For example, animals can be classified as mammals, birds, fish, reptiles, or amphibians.
2. Numerical: This type of classification involves grouping items based on numerical values or measurements. For example, data can be classified into groups based on ranges of values (e.g. 0-10, 11-20, 21-30).
3. Hierarchical: This type of classification involves grouping items into a hierarchical structure, with broader categories at the top and more specific subcategories below. For example, a hierarchical classification of animals might include the categories of “vertebrates” and “invertebrates” at the top level, with subcategories such as “mammals,” “birds,” “fish,” “reptiles,” and “amphibians” below.
4. Binary: This type of classification involves grouping items into one of two categories, typically based on true/false or yes/no criteria. For example, data can be classified into two groups, one with a certain characteristic and one without.
5. Multiclass: This type of classification is used when there are more than two classes. In machine learning, it is used to predict the output in multiple categories.
6. Clustering: This type of classification is used in unsupervised learning; it is used to group similar data points together in clusters.

Importance of Classify

Classifying is an important concept in mathematics that helps students to understand and organize different shapes and numbers. It is a process of grouping similar objects or things together based on their characteristics or properties.

In biology, classification is used to organize living organisms into groups based on their characteristics. The most widely accepted classification system is the Linnaean system, which Carl Linnaeus developed in the 18th century. 

This system classifies living organisms into different taxonomic groups such as kingdom, phylum, class, order, family, genus, and species.

In computer science, classification is used in machine learning, which is a field of artificial intelligence that deals with the development of algorithms that can learn from data. Machine learning algorithms are used to classify data into different categories based on their characteristics. 

For example, an algorithm could be trained to classify emails as spam or not spam.

Conclusion

Classification is a process of organizing and grouping things based on their shared characteristics or properties. It is used in various fields, such as mathematics, biology, computer science, and engineering. 

It helps in the understanding and analysis of data by grouping it into different categories. Classification is an essential concept in mathematics that helps students to understand and organize different shapes and numbers.

 It is a powerful tool that helps to identify patterns and relationships between different mathematical objects, making it easier to learn and study mathematics. Understanding classification will help students to become more proficient in math and allow them to approach more advanced mathematical concepts with more ease.

Three Examples of Classification in Mathematics

Example 1

How can you classify polygons?

Solution

In mathematics, classification organizes shapes according to their specific properties.

Polygons can be classified according to their number of sides. Triangles have three sides, quadrilaterals have four sides, pentagons have five sides, and so on. This is known as the polygon classification system. 

Example 2

Is it possible to group numbers based on certain features? How can it be done?

Solution

Another example of classification in mathematics is the classification of numbers. Numbers can be classified into several categories, such as natural numbers, whole numbers, integers, rational numbers, and irrational numbers. 

Natural numbers are the numbers that are used to count objects and are positive integers (1, 2, 3, 4). Whole numbers are natural numbers, along with the number zero (0, 1, 2, 3, 4). Integers include both positive and negative whole numbers (-3, -2, -1, 0, 1, 2, 3). 

Rational numbers are numbers that can be expressed as the ratio of two integers (e.g., 3/4, 22/7, etc.), while irrational numbers cannot be expressed as a ratio of two integers (e.g., √2, π, etc.). By classifying numbers into different categories, students can understand their properties and how they relate to each other.

Example 3

How can we classify the nature of the roots of a quadratic equation using a numerical equation?

Solution

A quadratic equation is an equation of the form ax² + bx + c = 0, where a, b, and c are constants. The solutions to this equation, also known as the roots, can be found using the quadratic formula:

\[ x = \frac{-b \pm \sqrt{b^2-4ac}}{2a} \] 

The nature of the roots can be determined by the value of the discriminant, b² – 4ac. If the discriminant is positive, the equation has two distinct real roots. If the discriminant is zero, the equation has one double real root. If the discriminant is negative, the equation has no real roots, only complex roots.

For example, consider the equation 2x² + 5x – 3 = 0. Using the quadratic formula, we can find the roots:

\[ x = \frac{-5 \pm \sqrt{5^2 – 4(2)(-3)}}{22} \]

\[ = \frac{-5 \pm \sqrt{25 + 24}}{4} \]

\[ = \frac{-5 \pm \sqrt{49}}{4} \]

\[ = \frac{-5 \pm 7}{4} \]

The roots are x = (-5 + 7) / 4 = 2/4 = 1/2 and x = (-5 – 7) / 4 = -12/4 = -3/2. 

Since the discriminant, b² – 4ac = 5² – 42 * (-3) = 25 + 24 = 49, is positive, the roots of the equation are real and distinct.

All images were created with GeoGebra.

Class Interval Definition < Glossary Index > Clockwise Definition