JUMP TO TOPIC
Column Addition|Definition & Meaning
Definition
The most common and basic method used for adding numbers by writing them in columns over each other is called column addition. In this method, numbers are vertically stacked such that the digit in units place is over each other for all operands and similarly for all the other digits. The numbers are then added 1 digit at a time, starting from the right (unit’s place) and moving towards the left. Each step may produce a carry if the sum is a two-digit number which is carried onto the next addition on the left.
Figure 1 shows the column addition of two one-digit numbers.
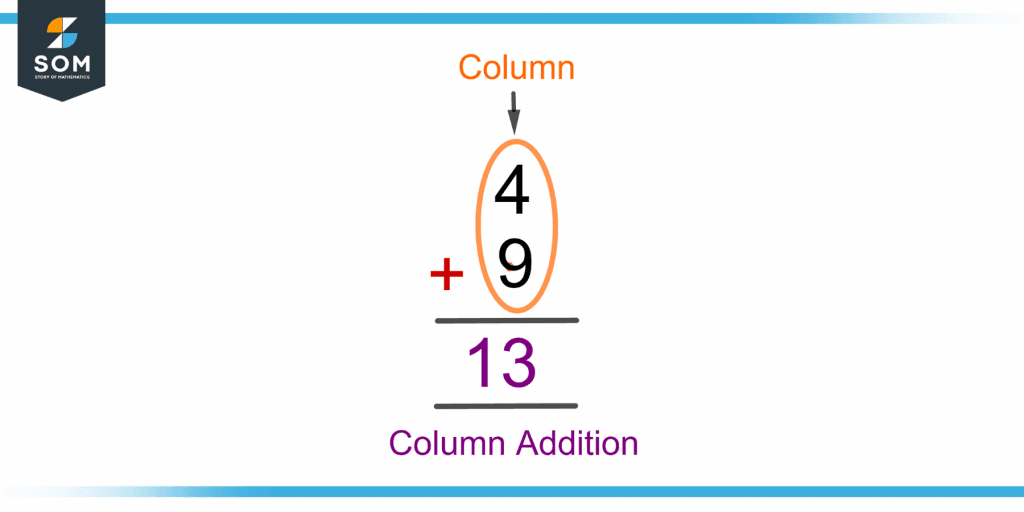
Figure 1 – Demonstration of Column Addition of Two Numbers
Addends
The word “addend” comes from the Latin word “addendum,” which means “to be added.” For example, in the expression given below:
12 + 34 + 16 + 8
The numbers 12, 34, 16, and 8 are the addends as they are being added together.
In column addition, the addends are written one over the other in a column such that the digits of units, tens, hundreds, etc., place of all the addends align in each column.
For example, in the above equation, the two-digit numbers 12, 34, 16, and 8 have the digits in the units place as 2, 4, 6, and 8 and in the tens place as 1, 3, 1, and 0, respectively. In the tens place of 8, 0 can be written, or the space can be left empty.
Augend
The first addend while writing an addition expression or equation is known as the “augend.” For example, in the expression:
5 + 7 + 10
The augend is 5; the augend can also be 7 or 10 if the order of the addends is changed. This is because the addition process holds commutative and associative properties.
Sum
The result obtained after the addition process is known as the sum. An addend is also known as a “summand” as it includes the word “sum.” For example, the sum of the summands 4, 7, and 8 is:
4 + 7 + 8 = 19
The sum of addends is found using column addition. For example, in the expression given under the “Addends” heading:
12 + 34 + 16 + 8
The sum of the column addition of 12, 34, 16, and 8 is shown in figure 2.
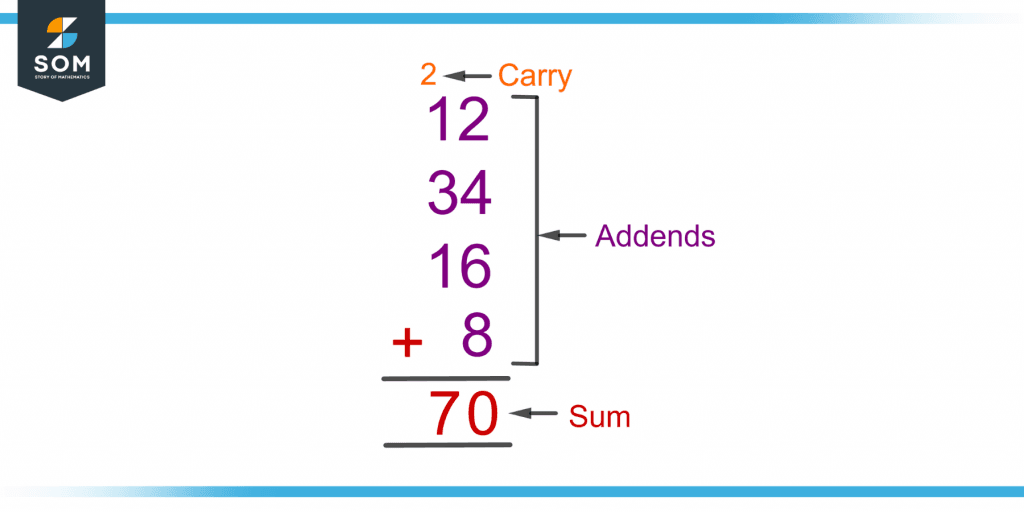
Figure 2 – Demonstration of Addends, Sum, and Carry in the Column Addition of Four Numbers
Properties of Addition
To perform column addition, the properties of addition should be known, which are discussed as follows:
Closure Property of Addition
The closure property of addition states that adding two natural numbers results in another natural number. The same is true for integers, decimals, fractions, and whole numbers. For example, adding decimals 1.3 and 2.5 results in another decimal, i.e., 3.8.
Commutative Property of Addition
The commutative property of addition states that changing the order of two addends does not have an effect on the sum of the addends. It means the two addends can be written in any order. If p and q are two addends, they can be added in any order, and the result will be the same as:
p + q = q + p
For example, two numbers, 16 and 21, are to be added. In column addition, either 16 can be written on top of 21 or the other way around; the sum does not change as addition holds the commutative property.
So,
16 + 21 = 21 + 16 = 37
Associative Property of Addition
The associative law of addition states that the sum does not change by changing the order of grouping of addends. If l, m, and n are three addends, then according to the associative property of addition:
l + (m + n) = (l + m) + n
It means that if l is added to (m + n) or (l + m) is added to n, the result will be the same. For example, the three addends 17, 23, and 33 can be grouped in any order to obtain the same sum, i.e., 73 as:
17 + (23 + 33) = (17 + 23) + 33
17 + 56 = 40 + 33
73 = 73
Additive Identity
The additive identity is a numerical value, when added to any number, gives the identity of that number. The additive identity is zero “0”, as it is the only number when added to any number, gives the same number. If g is any number, then
g + 0 = g
For example,
21 + 0 = 21
Additive Inverse
The additive inverse is the of a number that is the same number but with the opposite sign. It is such a number, when added to the original number, produces the sum of zero. It is the negation of the original number. So, the additive inverse of a is -a and vice versa. For example, in the equation:
10 – 10 = 0
The additive inverse of 10 is -10, and that of -10 is 10, as their sum produces zero.
Column Addition of One-digit Numbers
The column addition of a two one-digit number is the simplest form of addition. One-digit numbers are from 0 to 9. Two or more two one-digit numbers are placed separately in a column and added together.
For beginners, small lines are marked on the right side of the column, next to and equal to each number in the column. These lines are then counted to know the total or sum of all the numbers. The answer is written in alignment with the column. Small lines are skipped if the student learns the addition operation.
Column Addition of Two-digit Numbers
The two-digit numbers have the digit on the right side in the units or one’s place and the digit on the left in the tens place. The digits of the numbers in the units place and tens place are stacked separately in two columns. U or O denotes Units or Ones, and T denotes Tens. U is written on the top of the units column, and T is on top of the tens column.
The addition process is started from the right-most column(units column), and each column is dealt with separately. After adding the units column, similar to one-digit column addition, move towards the left to add the digits in the tens column. The total of every column is written below and in alignment with each column; thus, the final sum is obtained.
Concept of Carry
A carry can be generated if the sum of two numbers in a column is a two-digit number(greater than 9). In this case, the number in the tens place of the sum in a column is forwarded to the top of the next column. This number is known as “carry” as it is “carried” forward to the next column. This is done in order to remember to add the carry when the next column is added with it.
Column Addition of Three-Digit Numbers
Column addition of three-digit numbers is similar to two-digit numbers, with the addition of a hundred’s place. The hundreds place column is denoted by H and is written on top of the hundreds column. After the tens column is added, the hundreds column is added. Thus, column addition is performed from right to left, always starting from the unit’s place.
Numbers with different numbers of digits can also be added through column addition, keeping in mind to place the digits of each number correctly in the units, tens, hundreds, thousands, etc., column place.
Column Addition in Multiplication
The process of multiplication also involves column addition at the end if two two-digit numbers or more are being multiplied. At first, the unit place of the second number is multiplied by all the digits of the first number separately and written in a row from right to left.
Then, in the next row, after leaving a space in the units place, the tens place of the second number is multiplied by all the digits of the first number and written in a row. The columns are added to obtain the product. Figure 3 shows the multiplication of two numbers, 31 and 22.
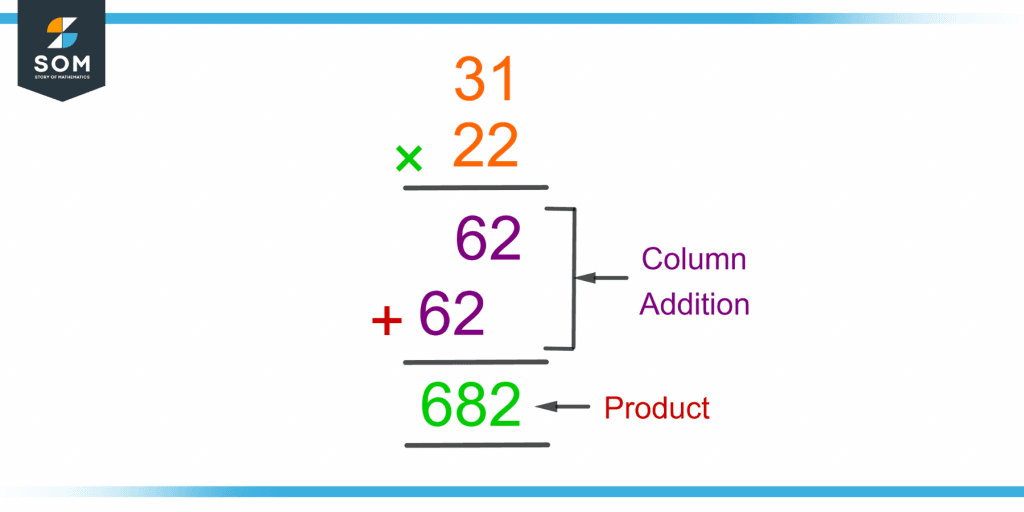
Figure 3 – Demonstration of Column Addition in the Process of Multiplication
Column Addition of Algebraic Expressions
Algebraic expressions can be added using column addition. Like terms are placed on top of one another in different columns so they can be added. Like terms have the same variables, the exponents of variables should also be the same.
For example, 3y2 and 5y2 are like terms as the variable y and its exponent, i.e., 2 are the same, and the coefficient can be different.
To add 4a2 + 2ab + 7b2 and 2b2 + 5a2 + 3ab, the like terms are placed in different columns, as shown in figure 4.
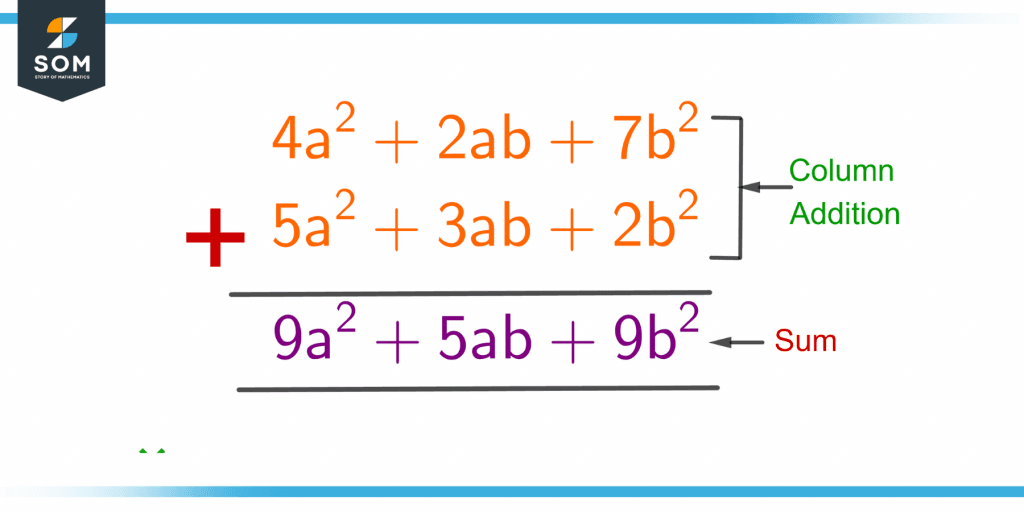
Figure 4 – Demonstration of Column Addition of Two Algebraic Expressions
Solved Examples of Column Addition
Example 1
Find the sum of 27, 52, and 369 using column addition.
Solution
Figure 5 shows the column addition of 27, 52, and 369.
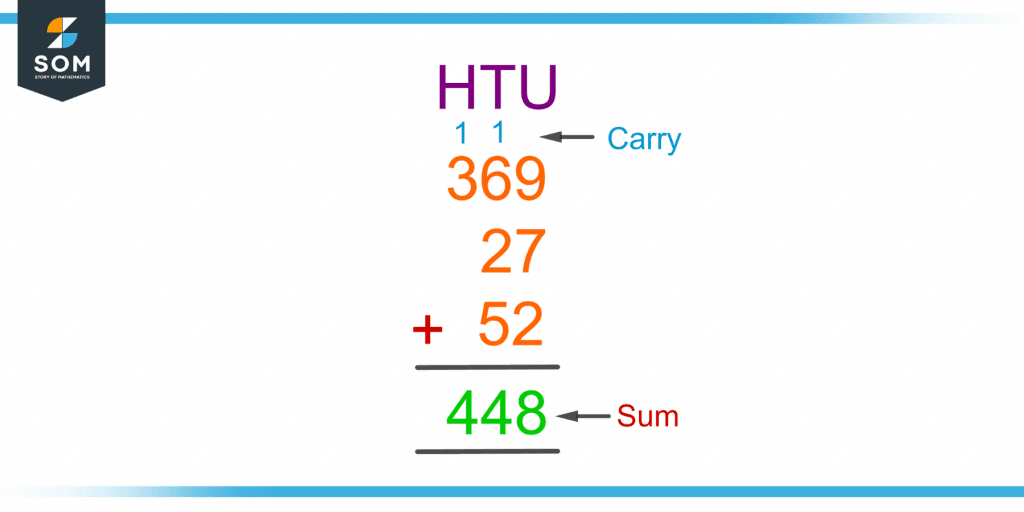
Figure 5 – Example of Adding Three Numbers by Column Addition
Hence, the sum obtained is 448.
Example 2
Two algebraic expressions are given below:
x3 + 3xyz + 4z2 + 2y + 4y2
3z2 + 5y + 3y2 + 5x3
Find the sum by using column addition.
Solution
At first, like terms should be separated and placed in columns. The terms x3 and 5x3, 4y2 and 3y2, 4z2 and 3z2, 2y and 5y are like terms. The term 3xyz has no like term, so it is placed separately with no term underneath it. Figure 6 shows the column addition of the two algebraic expressions.
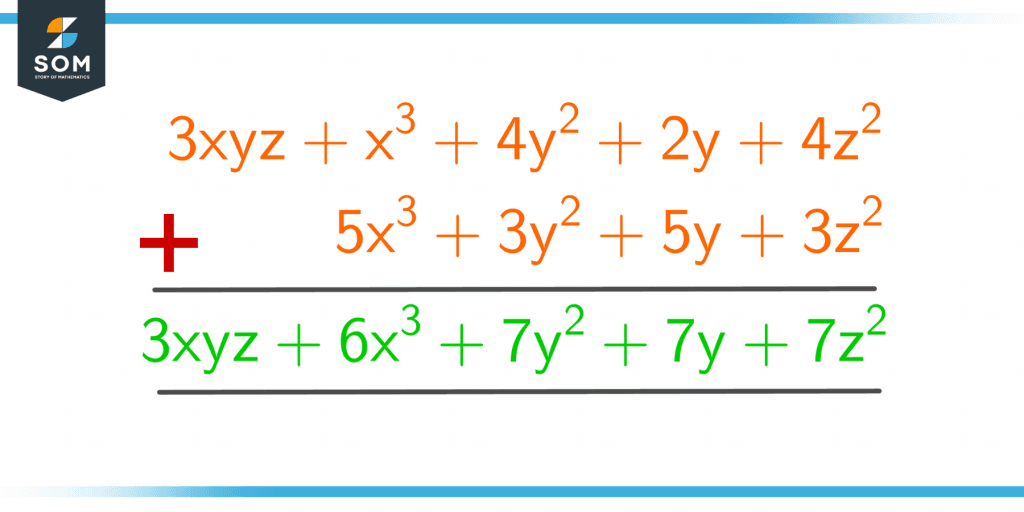
Figure 6 – Example of Adding Two Algebraic Expressions by Column Addition
All the images are created using GeoGebra.
