JUMP TO TOPIC
Concentric Circle|Definition & Meaning
Definition
If two objects in geometry have a common center, they are deemed to be concentric. Due to their shared center, regular polygons and circles are all concentric. In Euclidean geometry, two concentric circles always have different radii but the same center.
The Meaning of Concentric Circles
The circles that share a center are referred to as concentric circles, and they each have their own unique radius and consequently, circumference. To put it another way, it is described as two or even more circles sharing the same center point. The space between the circumferences of two concentric circles is called the annulus.
The following diagram depicts a figure with two concentric circles with a common center O.
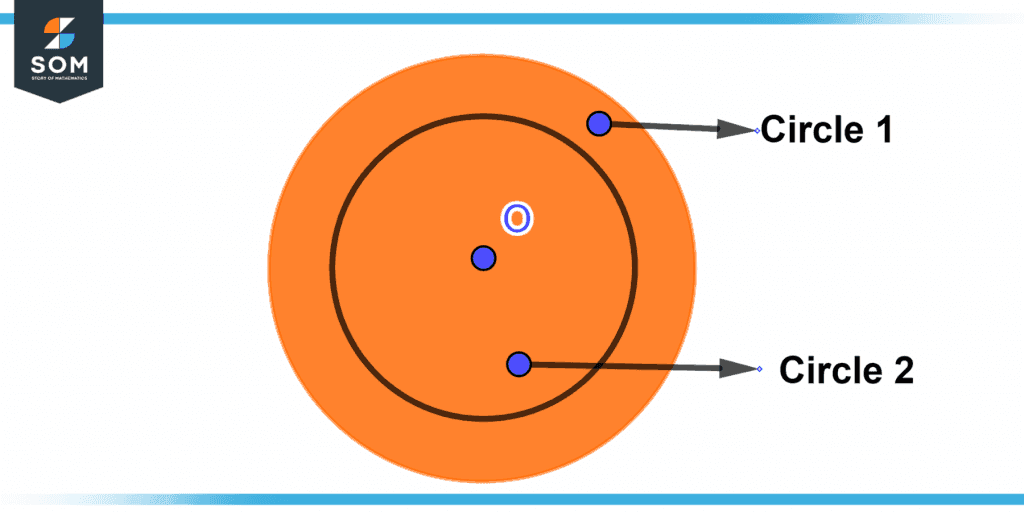
Figure 1 – Concentric circles.
By selecting the inversion center as one of the restricting points, any two circles could be formed concentric by inversion.
Examples of Concentric Circles Taken from Real Life
Have you ever looked at the wheel that’s on the ship? It consists of two concentric rings that are connected by spokes. Darts have been played by a good number of us. In addition, there are concentric circles on a dartboard. The circles on the dartboard were drawn around the bull’s eye, which serves as the standard middle of the line.
What Is the Annulus?
The region that is between two concentric circles is known as an annulus. An annulus is a name given to the space that is created by the intersection of two concentric circles. It has the shape of a ring but is flattened out. It is possible to determine the area of an annulus by first determining the size of the outer ring and then the area of the inner circle. To acquire the result, we need to calculate the difference in an area that exists between the two circles. The annulus is depicted in the following illustration by the portion that is shaded.
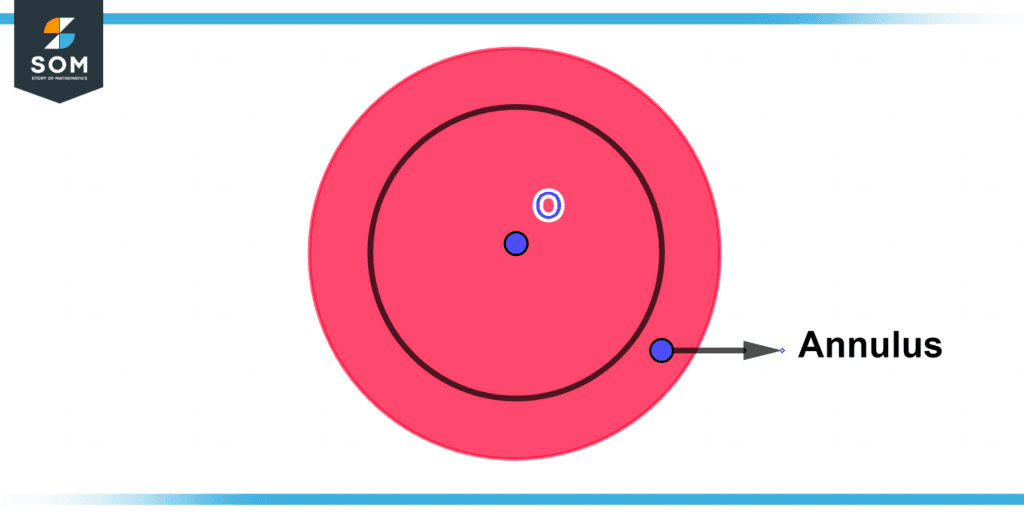
Figure 2 – Annulus of concentric circles.
Look at figure 3. When we subtract the area of a smaller circle from that of a larger circle, we are able to calculate the area of an annulus, also known as the blue zone. The value of r is used to indicate the radius of a smaller circle, whereas R is used to indicate the radius of a larger circle. Consequently, the following formula can be used by us in order to calculate the area of an annulus:
(πR)2 – (πr)2 = π (R2 – r2)
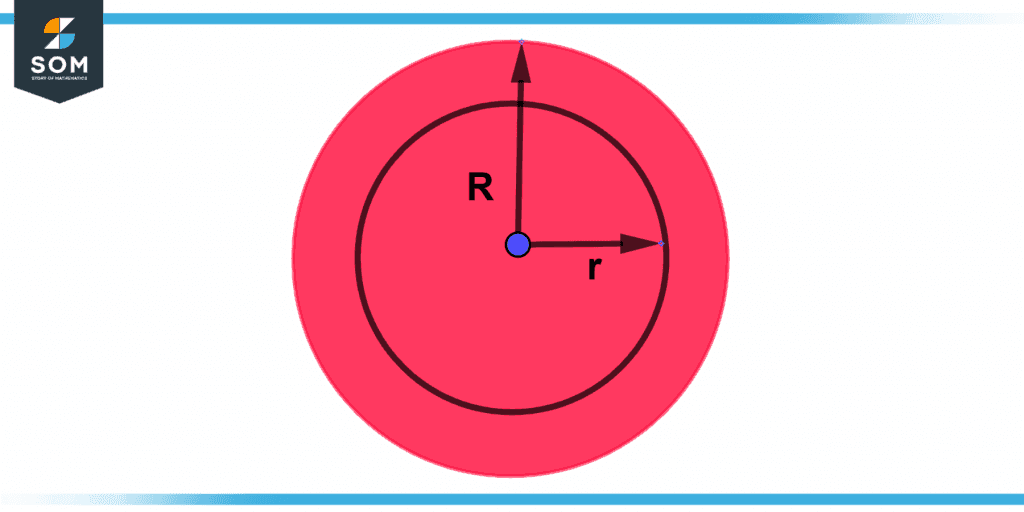
Figure 3 – Annulus formula
Important Points on Annulus
- The center of each concentric circle’s points is always the same.
- If two concentric circles overlap one another, then the radii of those circles will be equal.
- The region enclosed by 2 concentric circles is known as the annulus.
Can There Be More Than Two Concentric Circles?
It is possible to have more than two concentric circles. In fact, there can be infinitely many concentric circles around the same center point. The standard equation of a circle with radius r and center offset from the origin (a, b) :
(x – a)2 + (y – b)2 = r2
Consider a set of n circles c1, c2, …, cn with distinct radii r1, r2, …, rn and equal center offsets such that a1, a2, …, an = a and b1, b2, …, bn = b. Then, these circles are concentric with respect to the center point (a, b).
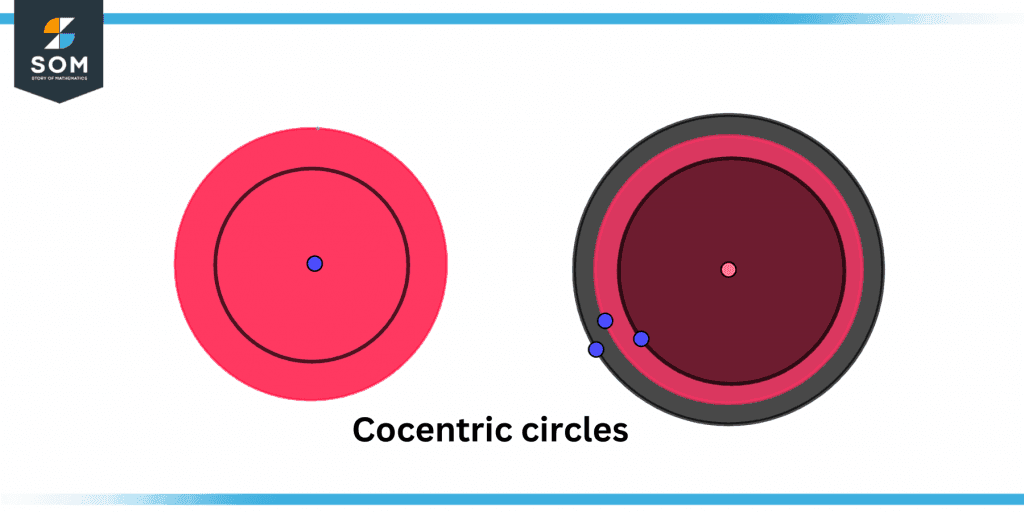
Figure 4 – Two concentric circles (left) and three concentric circles (right).
Numerical Examples of a Concentric Circle
Example 1
How much area does an annulus with an outside radius of 22 cm and an inner radius of 15 cm have?
Solution
Given that:
The outer radius is 22 cm.
The inner radius is 15 cm.
To find:
The area of annulus.
Since the area of a circle is:
Area = $\pi$ R$^2$
For the outer circle, the area is:
Area = $\pi$ R$^2$
By putting values, we get:
Area = 3.14 x 22 x 22
By calculating, we get:
=1519.76 cm$^2$
For the inner circle, we know that:
Thus annulus area is:
= 1519.76 – 813.26
= 706.5 cm$^2$
Example 2
How much area does an annulus with an outside radius of 52 cm and an inner radius of 25 cm have?
Solution
Given that:
The outer radius is 52 cm.
The inner radius is 25 cm.
To find:
The area of annulus. Again, using the formula for the area of a circle:
Area = $\pi$ R$^2$
For the outer circle, the area is:
Area = $\pi$ R$^2$
By putting values, we get:
Area = 3.14 x 22 x 22
By calculating, we get:
= 8490.56 cm$^2$
Thus annulus area is:
area of annulus = outer circle area – inner circle area
By putting values, we get:
= 8490.56 – 1962.5
= 6528.06 cm$^2 $
Thus the area of annulus for the given values is:
= 6528.06 cm$^2 $
All images/mathematical drawings were created with GeoGebra.
