JUMP TO TOPIC
Conclusion|Definition & Meaning
Definition
The term conclusion in maths is used to define us about the problem that we solve and when we produce the final result at the end then that stage of processes is called as conclusion.

Figure 1 – Give the Right Conclusion to the problem
When you solve a maths question, you have to end the problem by calculating the last answer and pulling a conclusion by writing the answer. A conclusion is the last step of the maths problem. The conclusion is the final answer produced in the end. The answer is completed by writing the arguments and statements by telling the answer to the question. The ending statement of a problem is called a conclusion.
Drawing conclusions refers to the act of thinking of interpreting a series of premises or some ideas and, from them, suggesting something that leads to a meaningful finding. It is normally regarded as a conscious way of learning.

Hypothesis and Conclusion
As a rule, a mathematical statement comprises two sections: the first section is assumptions or hypotheses, and the other section is the conclusion. Most mathematical statements have the form “If A, then B.” Often, this statement is written as “A implies B” or “A $\Rightarrow $ B.” The assumptions we make are what makes “A,” and the circumstances that make “B” are called the conclusion.
To prove that a given statement “If A, then B” is said to be true, we will require some assumptions for “A,” and after doing some work on it, we need to conclude that “B” must also hold when “A” holds.
If we are asked to apply the statement “If A, then B,” firstly, we should be sure that the conditions of the statement “A” are met and true before we start to talk about the conclusion “B.”
Suppose you want to apply the statement “x is even $\Rightarrow$ x2 is an integer.” First, you must verify that x is even before you conclude that x2 is an integer.
If-then Statement
In maths, you will, at many times, confront statements in the form “X $\Leftrightarrow$ Y” or “X if and only if Y.” These statements are actually two “if, then” statements. The following statement, “X if and only if Y,” is logically equivalent to the statements “If X, then Y” and “If Y, then X.” One more method for thinking about this kind of explanation is an equality between the statements X and Y: so, whenever X holds, Y holds, and whenever Y hold, X holds.
Assume the example: “x is even $\Leftrightarrow$ x2 is an integer“. Statement A says, “x is even,” whereas statement B says, “x2 is an integer.” If we get a quick revision about what it suggests to be even (simply that x is a multiple of 2), we can see with ease that the following two statements are identical: If x=2k is proved to be even, then it implies x2=2k2=k is an integer, and we know that x2=k is an integer, then x=2k so n is proved to be even.
In day-to-day use, a statement which is in the form “If A, then B,” in some cases, means “A if and only if B.” For example, when people agree on a deal, they say, “If you agree to sell me your car for 500k, then I’ll buy from you this week” they straightaway mean, “I’ll buy your car if and only if you agree to sell me in 500k.” In other words, if you don’t agree on 500k, they will not be buying your car from you.
In geometry, the validation or proof is stated in the if-then format. The “if” is a condition or hypothesis, and if that condition is met, only then the second part of the statement is true, which is called the conclusion. The working is like any other if-then statement. For illustration, the statement “If a toy shop has toys for two age groups and 45 percent of toys in the shop are for 14 or above years old, then 55 percent of the toys in the shop are for 13 and fewer years old.” The above statement concludes that “55 percent of the toys in the shop are for 13 and fewer years old.”
A implies B
In maths, the statement “A if and only if B” is very different from “A implies B.” Assume the example: “x is an integer” is the A statement, and “x3 is a rational number” is the B statement The statement “A implies B” here means “If x is an integer, then x3 is a rational number.” The statement is proven to be true. On the other hand, the statement, “A, if and only if B,” means “x is an integer if and only if x3 is a rational number,” which is not true in this case.
Examples of Drawing Conclusions
Example 1
Consider the equation below. Comment if this equation is true or false.
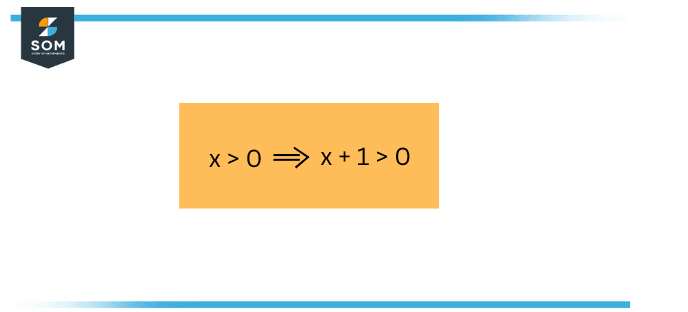
Figure 3 – Example Problem
Solution
To calculate its true answer, first, consider the hypothesis $x>0$. Whatever we are going to conclude, it will be a consequence of the truth that $x$ is positive.
Next, consider the conclusion $x+1>0$. This equation is right, since $x+1>x>0$.
This implies that the provided inequality is true.
Example 2
Simplify the below problem by providing a conclusion by calculating the answer of A.
\[ A= \dfrac{35}{3} \]
Solution
The expression given in the question is: $A= \dfrac{35}{3}$
Calculating the answer of A to make a conclusion, The arithmetic operation division is found in the question that is to be figured out in the provided problem. After figuring out the answer to expression A, The conclusion will be given.
\[ A= \dfrac{35}{3} \]
\[ A= 11. 667 \]
Therefore, we conclude the question by calculating the answer of $A=11.666$
Example 3
Consider the equation $0>1 \Rightarrow sinx=2$. Is this equation true or false?
Solution
To calculate the correct answer, first consider the hypothesis $0>1$. This equation is clearly false.
Example 4
calculate the below problem by providing a conclusion by estimating the value of X.
\[ 3+8 \times 2\]
Solution
The expression given in the problem is $3+8 \times 2 $.
Multiplication and Plus operation is to be carried out to calculate the answer to the given problem. After figuring out the answer to X the conclusion will be given.
\[ 3+8 \times 2\]
\[ 3+ 16\]
\[ 19\]
Thus, we conclude the example by calculating the value of $X = 19$.
All images/mathematical drawings were created with GeoGebra.
