JUMP TO TOPIC
Cone|Definition & Meaning
Definition
A cone is a three-dimensional geometric structure that starts from a circular base and converges as you move up to a point known as the apex. It can also be described as a circle that is moving up while continuously decreasing in radius till it reaches zero. The circle part of the cone is known as the base and the pointy end of the cone is called the apex.

Figure 1: The cone here is shown with a circle as a base and an endpoint called the apex.
These cones are usually formed by taking a line segment from every point of the circumference and joining it at the apex point over the circle. This creates a circular surface area and shape that is considered a cone.
Geometrically, cones are considered one of the sub-basic shapes and are easy to construct. They bear similarities with pyramids with the only difference being that the pyramids have a quadrilateral base as compared to a circular one of the cone.
Properties of Cones
Cones are considered easy-to-make shapes that have properties that make them different from other geometrical shapes. A cone will always have one circular face, which will be its base. It will never be considered a cone shape if the only face it has is not a circle.
Furthermore, having a circular base converging to one point, a cone will never have an edge, such as in a pyramid or a cubical shape. The lack of edges in the cone makes it smooth and sleek-looking with multiple real-life applications.
A cone is a convergence of points of a circle at one point in a different plane, hence it will have a third property of having only one vertex, that is the apex. A pyramid is similar in this regard in that it has one apex point but it also has other vertices on its base due to its quadrilateral base structure. Hence, a cone will only have one vertex.
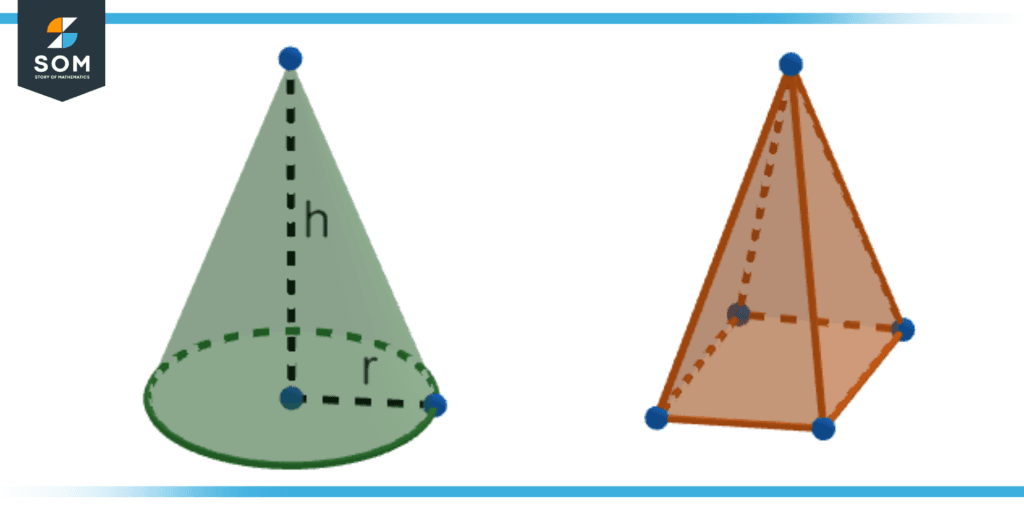
Figure 2: A cone and a pyramid are shown side by side.
Elements of a Cone
A cone consists of three core elements used to describe the cone’s properties:
- The radius of the circular base,
- Height of the apex from the base,
- The slant height of the apex from the circumference of the circle.
The radius of the base decides the size of the circle. This is explained to be the length of the line from the circumference to the center of the circle. The greater the radius, the larger will be the base of the cone.
The height of the cone is stated as the perpendicular distance of the apex from the base of the cone. This height is not necessarily taken from the center of the circle but it is taken perpendicular to the base straight up to the apex point.
Finally, the slant height is the line’s length from the apex point to the outer circumference of the circular base. The length of this slanted height can be calculated by using the Pythagorean theorem:
l$\mathsf{^2}$ = r$\mathsf{^2}$ + h$\mathsf{^2}$
Here, we have h denoting the height of the cone, l as the slant height, and the radius of the circular base denoted by r.
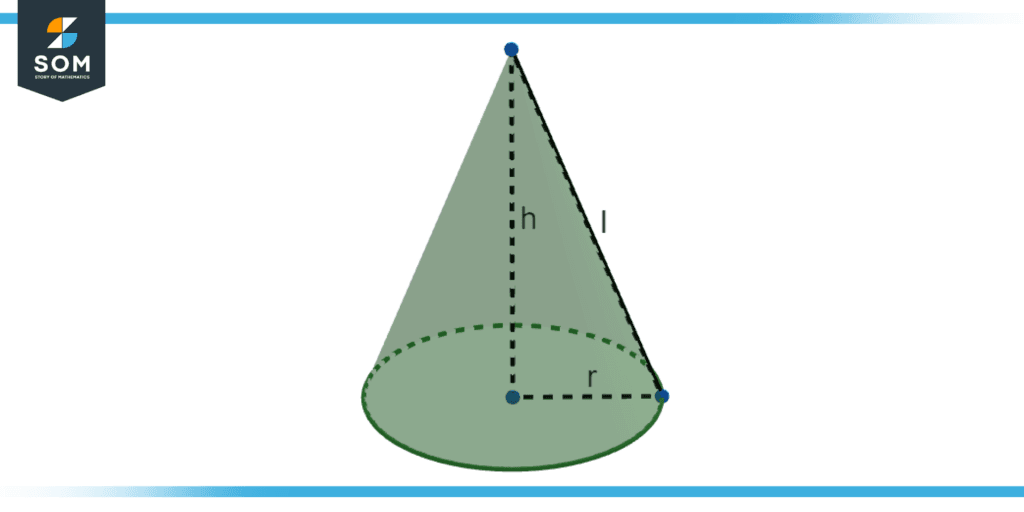
Figure 3: The elements of a cone are shown in this figure.
Important Formulae Regarding the Cone
A cone has properties that can be calculated using mathematical formulae: Total volume and Surface area. These two quantities are important to describe the cone’s implicit values and characteristics.
The surface area of the cone is described as the area of the outer shell of the cone. This includes the circular base’s area and the area of the curved surface of the cone. The formula for the curved surface area is derived as follows:
Curved Surface Area = $\pi$ x l x r
Where l is the slant height, r is the radius and $\pi$ is equal to 3.142. This curved surface area can be added to the area of the circular base $\pi r^2$ to form the following formula of the total surface area:
Total Surface Area = $\pi$ x r x l + $\pi$r$\mathsf{^2}$
Hence:
Total Surface Area = $\mathbf{\pi}$ x r(r + l)
The volume of the cone is the total amount of space the cone occupies or in easier terms, the quantity of liquid it can hold if the cone were to be hollow. The total volume of the cone can be calculated using a formula derived as follows:
Volume = $\dfrac{1}{3} \pi$ x r$\mathsf{^2}$ x h
Here, r and h respectively represent the radius of the circular base and the height of the cone. This formula is similar to the formula of a cylinder, but here we can deduce that the cone is always one-third of a cylinder of the same radius and height.
An Example of Cones Volume and Surface Area Formulae
A cone is given with a 10 cm height and a 5 cm radius. Find the total surface area and volume of this cone.
Solution
In this problem, the elements of the cone h = 10 cm and r = 5 cm. Using this data, we can calculate the slant height l of the cone with the help of the Pythagoras theorem.
l = $\mathsf{\sqrt{r^2 + h^2}}$
l = $\mathsf{\sqrt{5^2 + 10^2}}$
l = $\mathsf{\sqrt{25 + 100}}$
l = $\mathsf{\sqrt{125}}$
l = 11.18 cm
Thus, after finding the slant height, we can find the surface area of the cone as shown below:
Total Surface Area = $\pi$ x 5 (5 + 11.18)
Total Surface Area = $\pi$ x 5(16.18)
Total Surface Area = 254.16 cm$\mathsf{^2}$
Hence the total surface area is equal to 254.16 square cm.
Finally, the volume of the cone can be calculated as:
Volume = $\dfrac{1}{3} \pi$ x 5$\mathsf{^2}$ x 10
Volume = $\dfrac{1}{3} \pi$ x 25 x 10
Volume = $\dfrac{1}{3} \pi$ x 250
Volume = 261.80 cm$\mathsf{^3}$
Thus, the volume of the cone is calculated as 261.8 cubic cm.
All drawings and mathematical graphs are made using GeoGebra.
