JUMP TO TOPIC
Consecutive Numbers|Definition & Meaning
Definition
Consecutive numbers are those that come after one another in a predictable pattern or counting order. They are written in sequential order with the defined difference between the numerals and no gaps in between. In this tutorial, let’s study more about consecutive numbers.
What Are Consecutive Numbers?
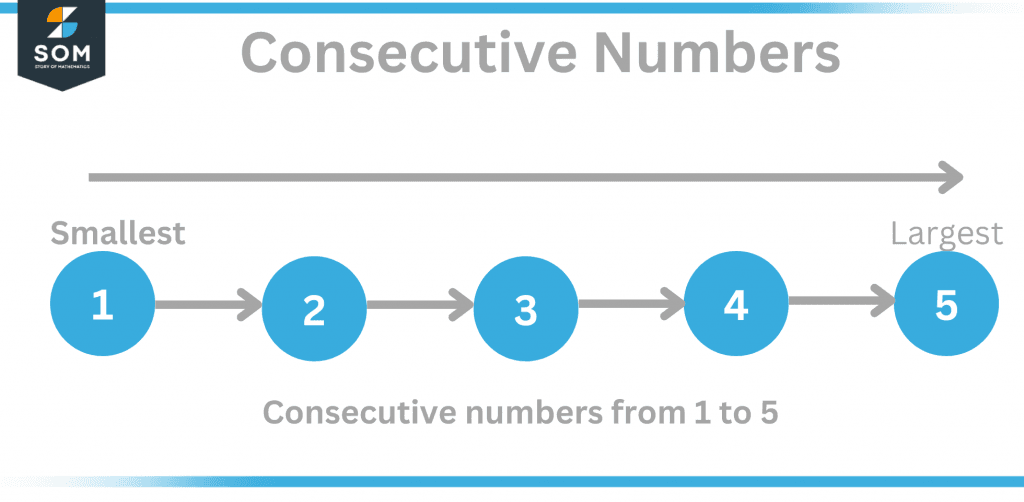
Figure 1 – Consecutive numbers
We must first understand the idea of predecessors and successors to comprehend consecutive numbers. The preceding number is always put before a number and is referred to as the predecessor. A number’s successor is the one that is written just after it. Consider the following natural numbers: 1, 2, 3, 4, and 5. 1 comes before (precursor) 2, and 2 comes after (successor ) one.
Consecutive numbers are those that come after one another in ascending sequence, from smallest to largest. The typical difference between every two numbers is 1. Remember that there is always a set difference between any predecessor-successor combination. Let’s examine a few instances of successive numbers.
The difference between any predecessor-successor pair in the aforementioned example is 1. The subsequent numbers in the series will be a, a+1, a+2, a+3, a+4, and so on if we use the symbol ‘a’ for the first number.
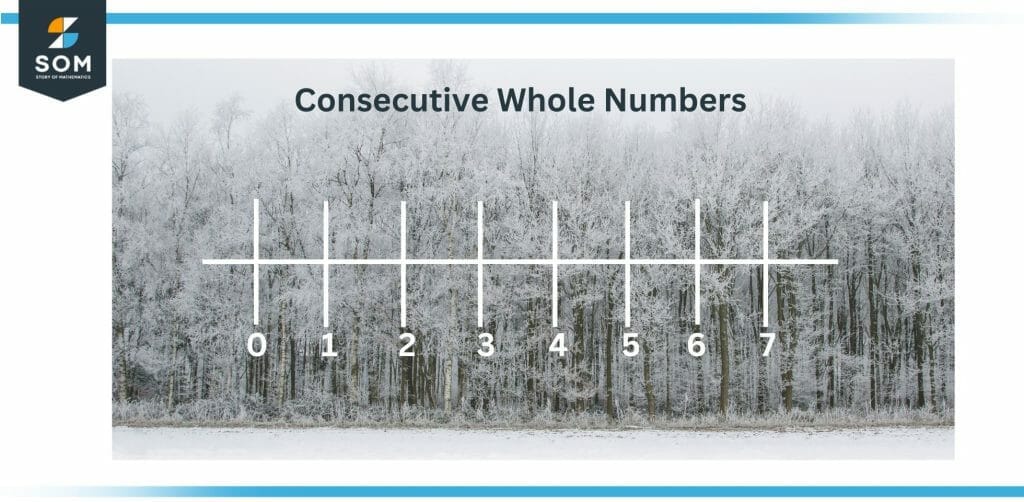
Figure 2 – Consecutive whole numbers
Consecutive Even Numbers
We are aware that even numbers are those with the following last digits: 0, 2, 4, 6, and 8. Let’s now take into consideration and write down the set of ascending even numbers from 2 to 12.

Figure 3 – Consecutive even numbers
The numbers are 2, 4, 6, 8, 10, and 12 when written from smallest to largest. We can observe that there is always a 2 difference between any pair of predecessors and successors. These figures, therefore, make up the list of succeeding even numbers.
Consecutive Odd Numbers
We are aware that odd numbers are those that cannot be divided in half by two. When we arrange them in ascending order, we can see that the difference between them is always 2. For instance, the numbers 3, 5, 7, 9, and 11 are referred to as consecutive odd numbers since each predecessor-successor combination has a difference of two, such as 7-9 = 2 and 11-9=2, and so on.

Figure 4 – Consecutive odd numbers
Consecutive Number Properties
The difference between any pair of predecessors and successors is fixed. If we write the initial number as n, the subsequent numbers in the sequence will be a, a+1, a+2, a+3, a+4, and so on. Any two consecutive odd numbers have a difference of 2. For instance, the difference between any two consecutive odd numbers in the series of 3, 5, 7, 9, and 11 is 2, so 5 – 3 = 2, 7 – 5 = 2, and so on.
Any two consecutive even numbers are divisible by two. For instance, any two consecutive even numbers in the series of even integers 4, 6, 8, and 10 are different from each other by 2, so 6-4 = 2, 8-6 = 2, and so on.
The sum of n succeeding numbers can be divided by n if n is an odd number. Consider the odd number sequence 5, 7, 9, 11, 13, 15, and 17 as an example. There are 7 numbers in the sequence. The property, therefore, dictates that these consecutive odd integers should add up to a number that can be divided by 7.
11+13+15+17+5+7+9= 77.
This property is satisfied by 77/7 = 11.
Here, it’s important to notice that this property only holds true if n is an odd number, or, more specifically, if the sequence only contains odd numbers.
Any two integers added together will always be an odd number. As an illustration, think about the numbers 1, 2, 3, 4, 5, 6, 7, and 8. The two consecutive numbers in this case will always add up to an odd number. 6 + 7 = 13, 7 + 8 = 15, 4 + 5 = 9, etc.
Two successive odd integers added together always equal an even number. Consider the odd number sequence 3, 5, 7, 9, 11, 13, 15, for instance. When two successive odd integers are added together, the result is always an even number. 9 + 11 = 20, 5 + 7 = 12, 7 + 9 = 16, etc.
When you add two even integers together, the result is always an even number. Take the even number sequence 12, 14, 16, 18, 20, 22, and 24 as an illustration. In this case, the result of adding two successive even integers will also be an even number. 12 plus 14 equals 26, followed by 14 plus 16, and so on.
The Formula for Consecutive Numbers
The following two numbers are (n + 1) and (n + 2) for an integer n. More formulas for consecutive numbers are provided below.
The equation for adding “n” numbers in a row is [a + (a + 1) + (a + 2) +…. a + (n-1)].
As a result, (n/2) (first number + last number) is the sum of “n” consecutive numbers or “n” terms of AP (Arithmetic Progression).
The formula for Even Consecutive numbers: 2n, 2n+2, 2n+4, 2n+6,…
The formula for odd consecutive numbers: 2n+1, 2n+3, 2n+5, 2n+7,…
Important Points
The following set of key ideas should be kept in mind when working with consecutive numbers.
Write the numbers in ascending order and then calculate the difference between any predecessor-successor combination to identify the missing numbers in the series.
If we denote the first number as a, the subsequent numbers in the series will be a+1, a+2, a+3, a+4 and so on.
If we indicate the first integer as a, the subsequent event or sequential odd integers will be a+2, a+4, a+6, a+8, and so on.
The general formula for an odd consecutive number is 2a+1, where a is any positive integer.
The general formula for an even consecutive number is = 2a (where ‘a‘ is any integer).
Examples of Consecutive Numbers
Example 1
Locate the omitted digit from the following series: 4, 8, 12,…, 20, 24, 28, 32.
Solution
Any predecessor-successor pair in this series has a 4 difference between them. The missing number’s forerunner is 12, therefore The next number after the one that is missing is 20. The number that is lacking is: forerunner + difference = 12 + 4 = 16. Alternately, successor – difference = 20 – 4= 16 would be the missing number. Therefore, 16 is the series’ uncompleted number.
Example 2
If all of the given numbers are sequential multiples of an odd integer, what is the third number in the series? 5, 15, __ , 25, 30.
Solution
Any pair of predecessors and successors in this series differ by 5 from each other. The missing number’s forerunner is 15, therefore The next number after the one that is missing is 25. Predecessor + Difference = 15 + 5 = 20 is the missing number. Therefore, 20 is the omitted digit
Example 3
Twenty-four is the total of three consecutive even numbers. Which three numbers are they?
Solution
Even numbers that follow each other differ by two. The second and third numbers are n+2 and n+4, respectively, if the first number is n. Since their total is 24, we can deduce that n + n+2 + n+4 = 24. As a result, n equals 6, and 3n + 6 = 24. Thus, n = 6, n + 2 = 6 + 2, n + 4 = 6 + 4, and n + 2 = 6 + 2 = 10 are the numbers. Let’s now add the three numbers and check our answer. Thus, 10 + 8 + 6 = 24. The figures are therefore 6, 8, and 10.
All images/mathematical drawings were created with GeoGebra.
