JUMP TO TOPIC
Constant|Definition & Meaning
Definition
A constant is a fixed, unchanging value. For example, in 7x – 3 + 5 = 4, the constants are 3, 5, and 4. If the value of a constant is unknown, we represent it as a, b, c, etc., to indicate a fixed value. Even then, they do not behave like variables. However, a constant may change if the system’s conditions change (e.g., the boiling point of water changes as the altitude changes).
Constant in Algebraic Expressions
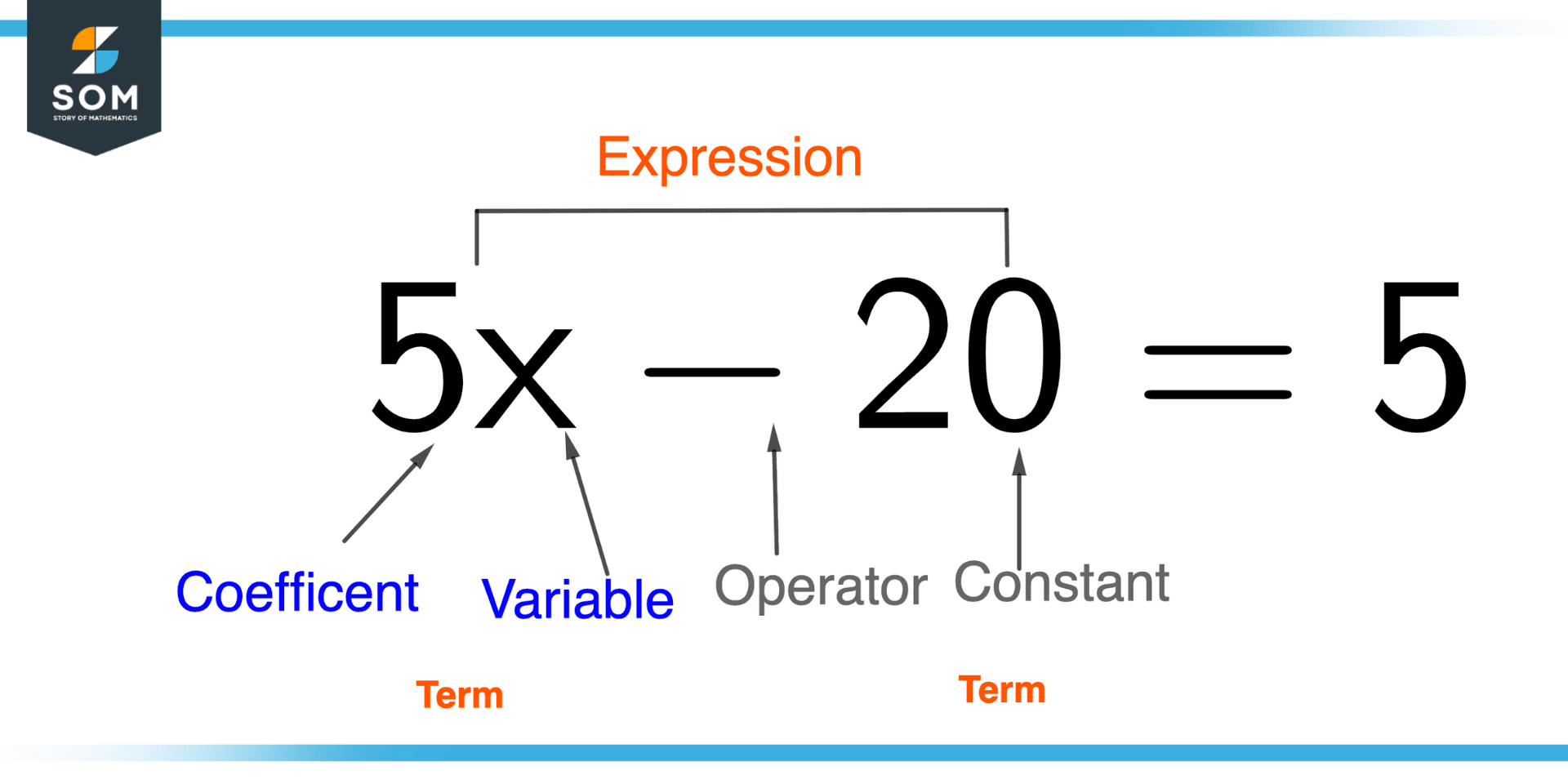
Figure 1 – Constant in Algebraic Expressions
In algebraic expressions, constants are values or symbols that don’t change during the computation. They are used to represent constant fixed values, such as “pi” or “e”, or specific numerical values that are given in a problem.
They can also be used to represent mathematical constants. A constant in an algebraic expression is typically denoted by a letter, like “c” or “k.” For instance, the constant number 2 is used to represent the y-intercept of the line denoted by the equation in the expression y = 3x + 2.
Types of Constants
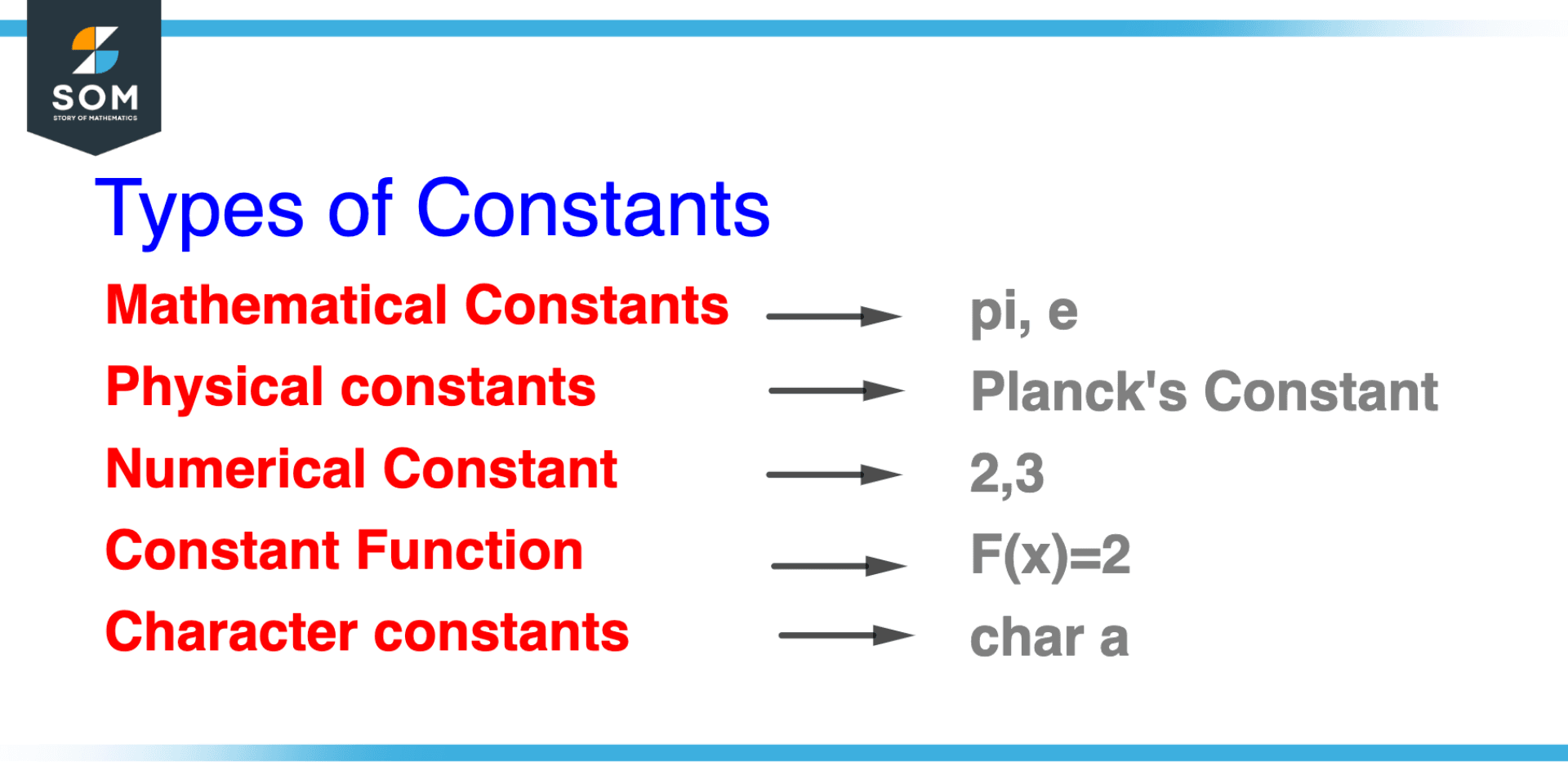
Figure 2 – Types of Constant
Numerous types of constants are employed in various contexts in mathematics, including:
- Mathematical Constants: Constants in mathematics are fixed numerical values that appear in a variety of mathematical formulas, such as pi or e.
- Physical constants: These are fixed numbers that stand in for physical constants like the gravitational constant, Planck’s constant, and the speed of light.
- Numerical Constant: The term “numerical constants” refers to specific numerical values, such as coefficients or arbitrary parameters, that are used in a particular problem or calculation.
- Constant Function: Functions that produce a constant value regardless of the input value are known as constant functions. For instance, the constant function f(x) = 2 always yields 2 and is referred to as a constant function.
- Character Constants: In computer programming, these symbols or characters are used to represent particular values, such as single letters, strings, or particular symbols.
Constant vs. Variable
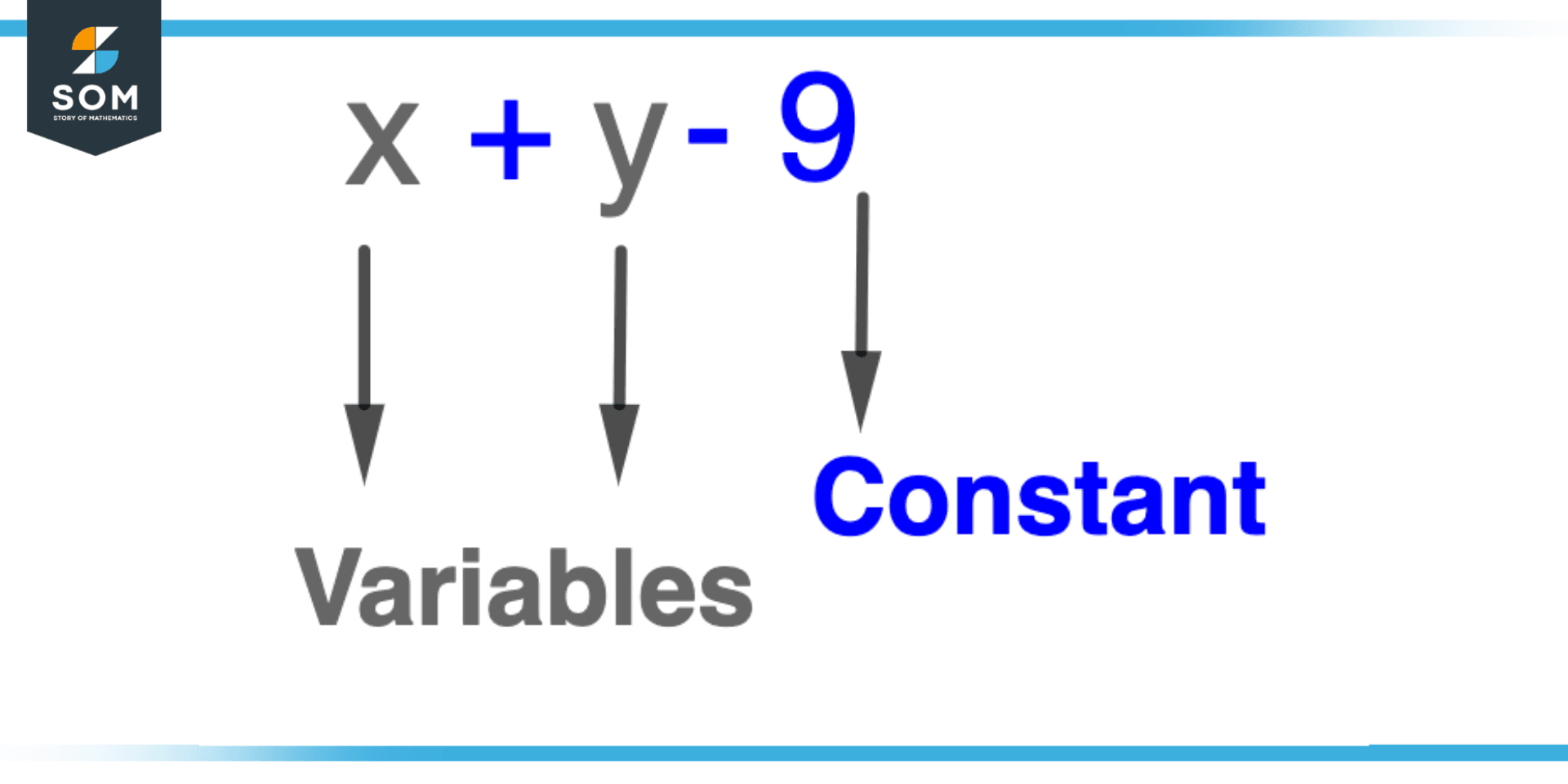
Figure 3 – Difference Between Constant and Variable
Constant
A constant is a value that does not alter over time or in response to different input values. Constants in mathematics are frequently denoted by symbols like pi , e, or by a particular numerical value like 2 or 5. Constants are used to represent fixed values that do not change, like the gravitational constant and the speed of light.
Variable
On the other hand, a variable is a value that can change or have different values assigned to it. Variables in mathematics are frequently denoted by letters like x, y, or z. For example, a person’s height or the number of apples in a basket are examples of values that can vary and are represented by variables.
In a nutshell, the primary distinction between constants and variables is that the former has fixed values that do not change, whereas the latter has variable values. Variables are used to represent values that can change, whereas constants are used to represent fixed values.
Properties of Constants
Following are a few properties of constants:
- Fixed Value: Regardless of the input or any other circumstances, a constant’s fixed numerical value never changes.
- Representation: Constants are frequently represented by Greek symbols or English letters like pi (π) and Euler’s number (e) or particular numerical values like 2, 7.5, etc.
- Immutability: Constants are immutable; they retain their original value throughout the course of a calculation or a program.
- Use in mathematical formulas: Fixed values like the speed of light, the gravitational constant, and Planck’s constant are represented by constants in a variety of mathematical formulas.
- Application in computer programming: Constants are used to represent particular values that never change, such as single characters, strings, or special symbols.
- Predefined Value: Constants frequently have predefined values. Examples include mathematical constants like π and e, as well as physical constants like the speed of light. These numbers have been calculated with great accuracy and are generally accepted.
These properties make constants a significant part of any mathematical equation or expression.
Use of Constants in Daily Life

Figure 4 – Applications of Constant
Constants are used in a variety of ways in daily life, frequently without our awareness. Here are a few illustrations:
- Timekeeping: In our daily lives, we measure time using the fixed length of a day. It is simple to keep track of time because a day is divided into 24 hours, and each hour is divided into 60 minutes which is constant.
- Navigation: To pinpoint a device’s location, navigation systems like GPS use the speed of light, a constant. In order to pinpoint a device’s location, the GPS system calculates the time it takes for satellite signals to reach the target.
- Cooking: The temperature constant, also known as the water’s boiling point, is used to calculate the cooking times for various foods. For instance, cooking eggs at a set temperature and time will result in either soft-boiled or hard-boiled eggs.
- Physics: When an object is falling, the velocity and position are calculated using the constant acceleration of gravity (g). This is applied in daily life when, for instance, designing roller coasters, figuring out how fast a projectile will travel, or figuring out how tall a building should be.
- Engineering: To calculate the properties of gases, such as pressure, temperature, and volume, engineers use the gas constant (R). This is crucial when designing engines, engines, and other systems that use gases, such as heating and cooling systems.
There are infinitely many more examples of constants we can observe in daily life.
Solved Examples Utilizing Constants
Example 1
Consider the equation of line y = 2x + 2. Find the value of y when x = 2(constant).
Solution
The equation y = 2x + 2 represents a line in this problem, with x serving as the independent variable and y serving as the dependent variable. The y-intercept of the line is symbolized by the constant number 2, which is used in the equation.
By substituting the value of x into the equation below, we can determine the value of y when x = 2.
y = 2 (2) + 2
y = 4+ 2
y = 6
Consequently, y equals 6 when x equals 2.
The y-intercept of the line is represented in this problem by the constant value of 2, which stays the same throughout the calculation.
Example 2
Consider a scenario where Andrew went to McDonald’s to buy snacks. After 3 years, he again went to McDonald’s and bought snacks. Which quantity in this scenario is constant, and which quantity is variable?
Solution
Constant
McDonald’s is a constant quantity in this scenario. At different times, he went to the same shop, i.e., McDonald’s, so that would be a constant.
Variable
Snacks may be variable as he might buy different snacks, and time is also a variable quantity.
All mathematical drawings and images were created with GeoGebra.
