Converse (Logic)|Definition & Meaning

Notation, Truth Table, and Other Details 

Usually, you will see the converse notated as A $\boldsymbol\leftarrow$ B rather than B $\boldsymbol\to$ A, but we use the latter frequently in this article. The following truth table shows that the converse and the original statement are only logically equivalent if the antecedent and consequent imply each other. All other cases are ambiguous.

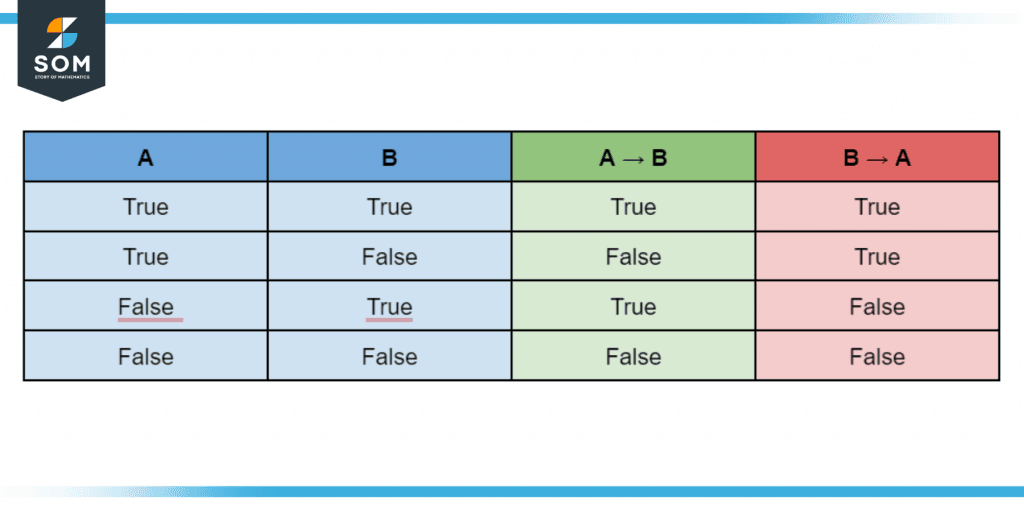
Figure 1 – Truth table indicating that a statement and its converse are logically equivalent if the constituents A and B imply each other.

The converse operation is often called “conversion.” It belongs in the same category of logical concepts as inverse and contrapositive, where, for a statement A $\to$ B:

• Converse: B $\to$ A or A $\leftarrow$ B
• Inverse: $\neg$A $\to$ $\neg$B
• Contrapositive: $\neg$B $\to$ $\neg$A

Remember that, unlike the converse and inverse, the contrapositive is always logically equivalent to the original statement. Further, the converse and inverse are logically equivalent, so if the converse is true, the inverse is also true. 

You can verify this using the fact that the converse and inverse have the same relationship as the original statement and the contrapositive.

Statements and Their Constituents

The constituents of the statement are called the antecedent (or hypothesis) and consequent (or conclusion). You can think of this as an if-then statement where: 

1. The “if” portion represents the antecedent
2. The “then” portion represents the consequent

Thus, a statement would look like “if this happens, then that happens.” Logically, “if x is true, then y is true.” 

Formally, we write a statement as A $\to$ B (contrapositives as $\neg$B $\to$ $\neg$A). For example, consider the statements: 

1. “If David has an apple, then he has fruit.” Here, the hypothesis is that David brought an apple, and consequently, he has fruit.
2. “If a polygon is three-sided, then it is a triangle.” In this statement, the hypothesis is that a polygon is three-sided, and the conclusion is that it is a triangle.
3. “If x is a natural number, it is a whole number.” Here, the antecedent is that we have a natural number x, and the consequent is that x is a whole number.

Keep these examples in mind as we analyze their converses in the coming sections.

Validity of the Converse

The validity of the converse of an implicational or categorical statement is not always guaranteed, even if the original was perfectly valid. 

The validity of the result of the conversion – much like inversion – depends on the mutual relationship of the constituent elements. For example, if other possible antecedents can lead to the same consequent, then the converse of the statement is likely false. 

Usually, the converse is only true if it does not imply or affirm anything other than the original statement. A statement whose converse is true is called a biconditional statement. 

From the earlier examples, we had the statement: “If a polygon is three-sided, then it is a triangle.” The converse would be: “A triangle is a three-sided polygon.” We can tell that it is true because a triangle is a three-sided polygon (by definition). Therefore, the converse is true, and the statement is biconditional. You can see this in the following figure:

Figure 2 – “If a polygon is three-sided, then it is a triangle” is a biconditional statement because its converse is true.

If the statements contain mutually inclusive terms, then the converse is true for those terms. We illustrate this below:

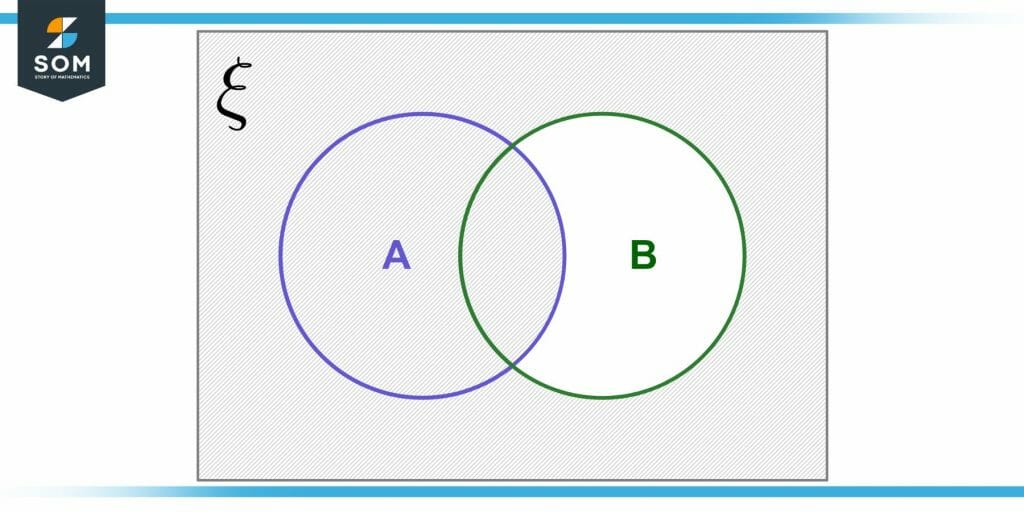
Figure 3 – Venn diagram for the converse A $\leftarrow$ B of a statement A$\to$ B where the constituents have mutually inclusive terms. The converse is invalid for the white region within B.

Keeping with the set logic, consider A a subset of B. Then, A $\to$ B is always true (anything in A automatically belongs to B), but the converse B $\to$ A is not necessarily true since some elements of B do not belong to A. Thus, B $\to$ A is only true for the lined part in the following figure:

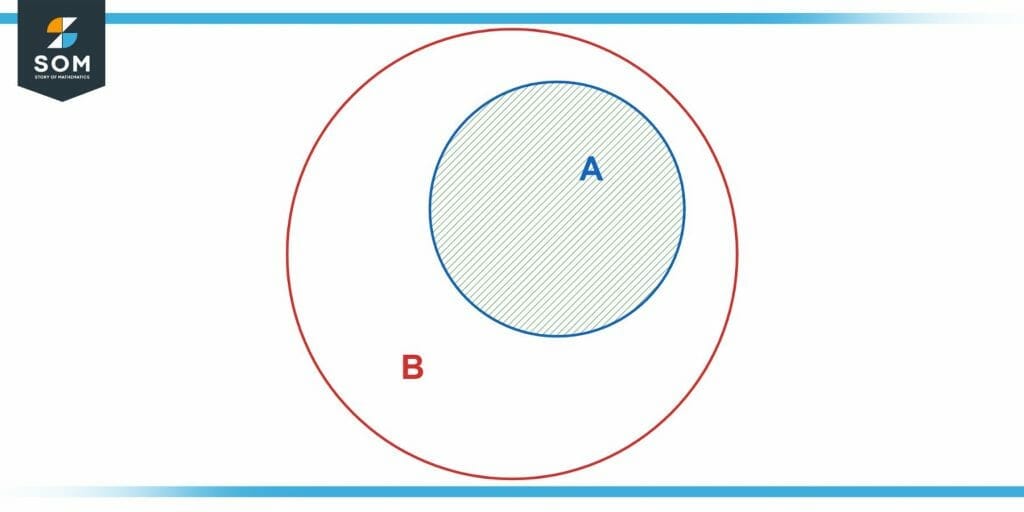
Figure 4 – If A is a subset of B, the converse of A $\leftarrow$ B is only true for the choice of B within A (the lined part).

If two sets are equal (every element in A belongs to B and every element in B belongs to A), then they completely imply each other. In logic, such a scenario is called biconditionality.

Figure 5 – Venn diagram depicting biconditionality; both sets A and B completely imply each other as they specify the same circle.

The Fallacy of Affirming the Consequent

A false converse is usually inferred from what is formally called the converse error or the fallacy of affirming the consequent. 

To understand the fallacy, consider the statement “a human is a mortal” and the converse, “a mortal is a human.” However, all living things are mortal! Therefore, for the original statement, there are other valid antecedents.

Now, consider the statement: “The lamp is broken, so the room is dark.” The converse is: “The room is dark, so the lamp must be broken,” which is invalid because, as shown in the figure, the room could be dark for various reasons. The lamp may not even be in the room! We illustrate the statement’s fallacy below:

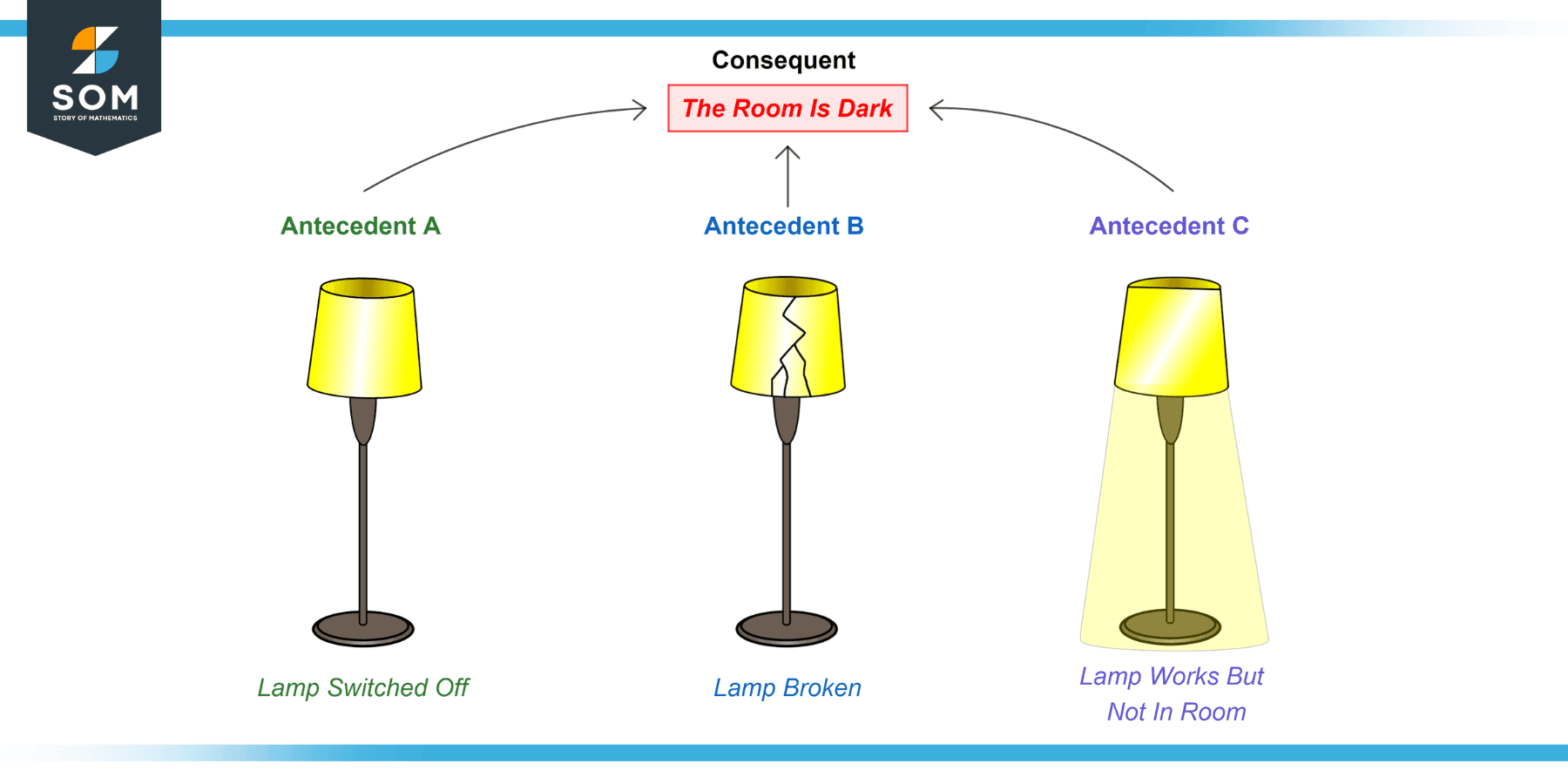
Figure 6 – The fallacy of affirming the consequent for a statement with multiple antecedents.

Ultimately, it is the absence of light that causes darkness. Thus, the bigger picture is that: “The room is dark because of the absence of a light source,” where the “absence of a light source” encompasses all possible antecedents at the cost of specifics.

For further clarification, let us see the converse of the first and third statements from the earlier section. The first statement is true because an apple is a type of fruit. Therefore, if David has an apple, he has fruit. 

However, the converse of the statement is “If David has fruit, then he has an apple,” which is not necessarily true. He could have a banana (which falsifies it), or he may adore apples and always bring them (which makes it true). Whatever the case, we can not know for sure.

Now, for the third statement, the converse is: “If x is a whole number, then it is a natural number.” Clearly, it is true for all x except for x = 0 because 0 is not in the set of natural numbers. Therefore, the converse is not necessarily true in this case either!

An Example of Finding the Converse

Verify the statement: “If Claire does not live in the US, then she does not live in New York.” Additionally, find its converse and state if it is true with reasoning.

Solution

First, we identify the hypothesis and conclusion. Let them be A and B.

A = Claire does not live in the US.

B = She does not live in New York.

Now, the statement S = A $\to$ B is true because New York is part of the US. Thus, if she is not in the US, she is definitely not in New York.

Let the converse of S be Q, then:

Q = B $\to$ A = A $\leftarrow$ B 

Q = “If Claire does not live in New York, she does not live in the US.”

Which is not valid! This is because New York is only part of the US – Claire could still be residing in another city within the US. Therefore, the converse of the given statement is not true.

All mathematical drawings and images were created with Geogebra.

Converse Logic Definition < Glossary Index > Convex Definition