Convex|Definition & Meaning

Convex Sets and Their Importance in Optimization 

In geometry, a subset of an affine space over the reals, or more broadly a subset of Euclidean space, is said to be convex if it contains the whole line segment connecting any two points in the subset. A subset that connects each line into a single line segment is known as a convex set or convex area (possibly empty). A solid cube is an example of a convex set, but anything hollow or depressed, such as a crescent shape, is not. This example of a convex and non-convex set is illustrated in figure 1.

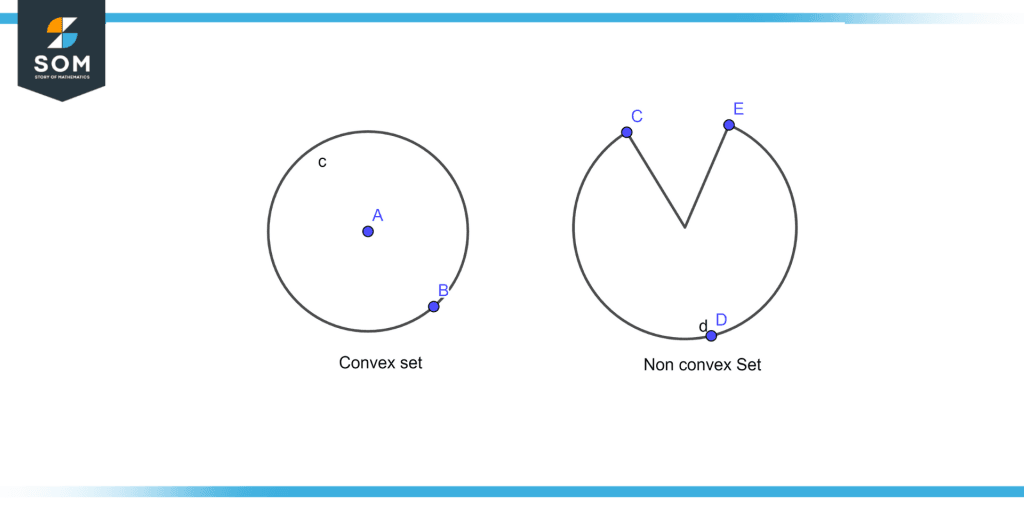
Figure 1 – Convex and non-convex set

An algorithm can be improved via convex optimization, which can hasten the rate at which it converges to the answer. Instead of computing a precise solution to the system, it may also be used to solve linear systems of equations.

Convex Functions

If the line segment connecting any two points on the function’s graph sits above the graph between the two points, the function is said to be convex in mathematics. A function is equivalently said to be convex if its epigraph the collection of points on or above the function’s graph is also a convex set. If and only if the second derivative of a single-variable twice-differentiable function is non-negative over the whole domain, the function is said to be convex. An example of a convex and non-convex function is illustrated in figure 2.

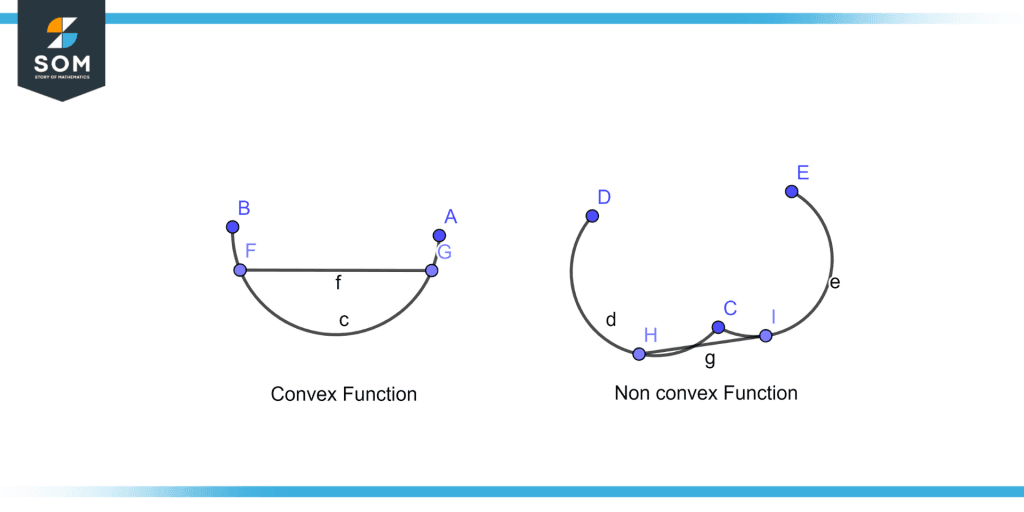
Figure 2 – Convex function and non-convex function

As illustrated in figure 2 in the convex function line segment f is above the function and in the non-convex function, line segment g is below the function.

Difference Between Convex and Concave Functions

The first derivative of a convex function increases, giving the appearance of an upward curve. A concave function, on the other hand, has a decreasing first derivative that causes it to bend downward. Examples of convex and concave function is illustrated in figure 3.

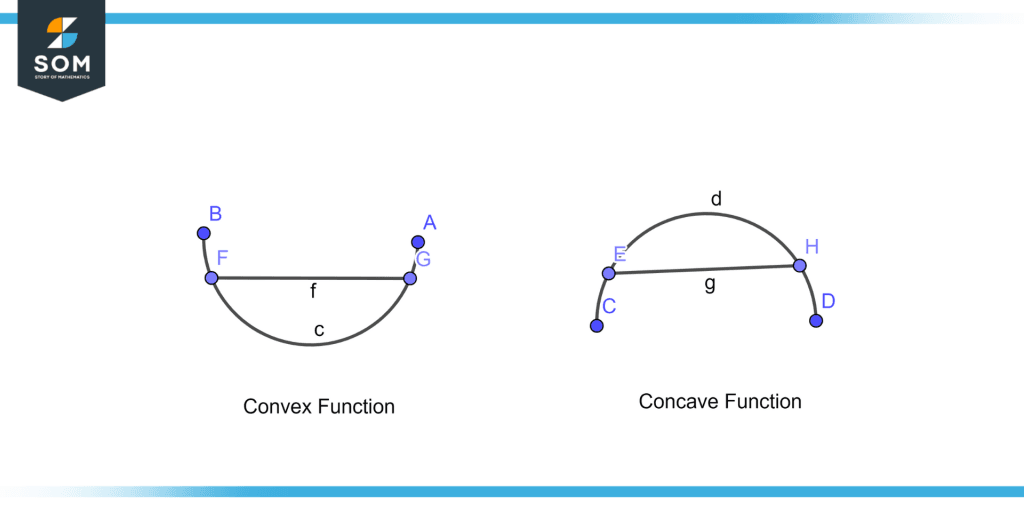
Figure 3 – Convex and concave function

Sufficient Conditions for Convexity and Concavity

Consider a function f(x) whose first derivative f′(x) occurs in the closed interval [a,b] and whose second derivative f′′(x) exists in the open interval (a,b). Consequently, the following prerequisites for convexity or concavity are met:

• If f′′(x)≥0 for all x∈(a,b),then the function f(x) is convex downward (or concave upward) on the interval [a,b].
• If f′′(x)≤0 for all x∈(a,b),then the function f(x) is convex upward (or concave downward) on the interval.

Operations That Preserve Convexity

In order to configure the set is convex by following rules

• X,Y belong to C, 0<=theta<=1 then (theta)x +(1- theta)y belong to C
• Show that C is obtained from simple convex sets that preserve convexity like intersection, affine function etc.

The intersection of any number of a convex set is convex illustrated in figure 4. In figure 4 the shaded region shows the intersection of two convex sets i.e. Euclidean ball and hyperplane.

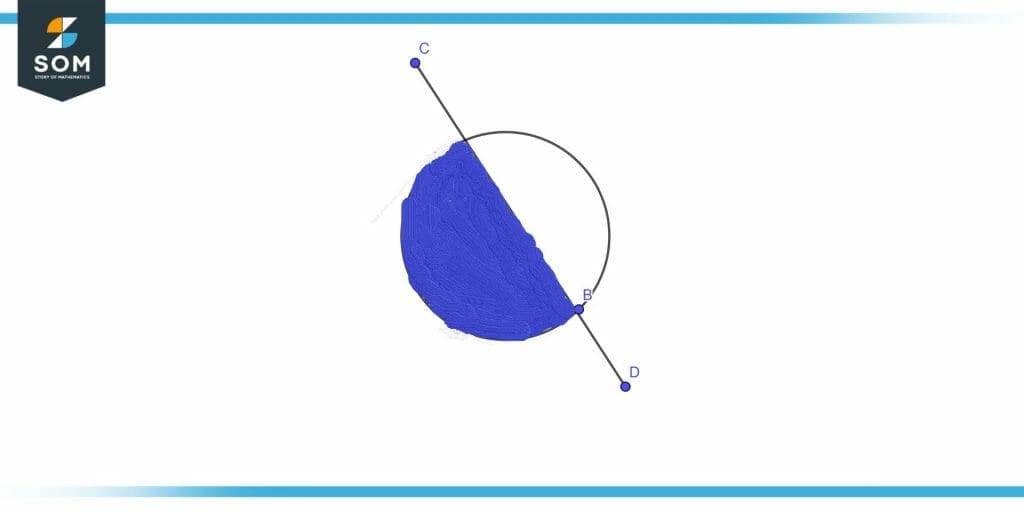
Figure 4 – Intersection of two convex sets

The affine functions Ax+b are the only functions that are both convex and concave. The same as images and inverse images of convex sets is also convex.

Difference Between Strictly and Non-strictly Convex Functions

A function is said to be strictly convex if the local minima are equal to the global minima, if the function in which local minima is not equal to the global minima, then the function is convex but it is not strictly convex. Figure 5 illustrates the difference between the convex and strictly convex functions.

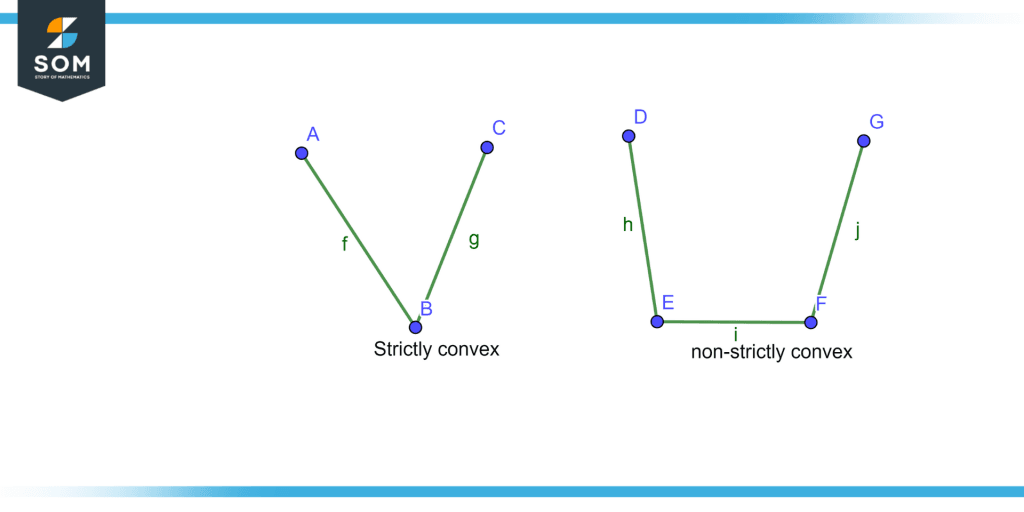
Figure 5 – Strictly convex and non-strictly convex

Practical Ways of Establishing Convexity of Function

In order to prove the function is convex we have the following practical solutions

• Basic definition (restriction of a function to the line).
• The function should be twice differentiable and the hessian of a function should be greater than or equal to zero.
• The function is obtained from the simple convex function by operations that preserve Convexity.

Importance of Convexity in Mathematics

Convex functions and convex sets are very important in many areas of mathematics. They are characterized by various useful properties and thus play an important role in investigating optimization problems. For example, a strictly convex function on an open set has only one minimum. Convex functions satisfy these properties even in infinite-dimensional space, if appropriate additional assumptions are included, making them the best-known functionals in the calculus of variations.

In probability theory, the expected value of a convex function of a random variable always defines the upper bound of the convex function that applies to the expected value of the random variable. From this finding, we can derive both the arithmetic-geometric mean inequality and Holder’s inequality, known as Jensen’s inequality.

Solved Problems Involving Convex Functions

Example 1

Check whether the Function $x^2$ is convex or not by calculating the Hessian of the function.

Solution

F(x)=$x^2$

F'(x)=2x

F”(x)=2

F’’(x) is greater than zero i.e. positive so the function is convex.

Example 2

Check whether the Function $e^x$ is convex or not by calculating the Hessian of the function.

Solution

F(x)=$e^x$

F'(x)=$e^x$

F”(x)= $e^x$

F’’(x) is greater than zero i.e. positive so the function is convex.

Example 3

Check whether the Function log(x) is convex or not by calculating the Hessian of the function.

Solution

F(x)=log(x)

F'(x)=$\dfrac{1}{x}$

F”(x)=$\dfrac{1}{x^2}$

F’’(x) is less than zero i.e. negative so the function is concave.

Example 4

Check whether the Function $\dfrac{1}{x}$ is convex or not by calculating the Hessian of the function.

Solution

F(x)=$\dfrac{1}{x}$

F’(x)=-$\dfrac{1}{x^2}$

F”(x)= $\dfrac{2}{x^3}$

F”(x) is greater than zero i.e. positive so the function is convex.

Example 5

Check whether the Function $e^x$-1 is convex or not by calculating the Hessian of the function.

Solution

F(x)= $e^x$-1

F'(x)= $e^x$

F”(x)=$e^x$

F”(x) is greater than zero i.e. positive so the function is convex.

All images/mathematical drawings were created with GeoGebra.

Convert Definition < Glossary Index > Coordinates Definition