JUMP TO TOPIC
Coordinates|Definition & Meaning
Definition
Coordinates are representative values of the distance of a point or object from a specific point or object used as a reference. The most common coordinates are the latitude and longitude coordinates which give the location of an object anywhere on the earth concerning the reference of the prime meridian located in Greenwich.
Theoretical Explanation of Coordinates
Coordinates are to address a point on a plane by using a pair of numbers. They are also known as math coordinates, which we use to make graphs. These coordinates are written in the form of ordered pair consisting of an x value and a y value (x, y) to give us a point to be used in a map or give directions.
This helps us to get the precise location of a point. The following example shows a point that tells us the exact position of a plane.
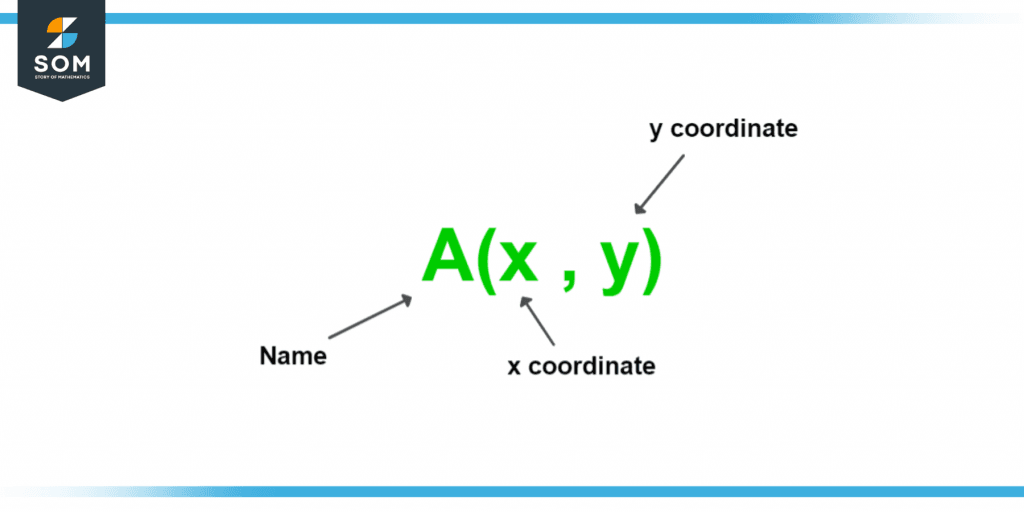
Figure 1 – Representation of Coordinates
In this example, we can see the ordered pair containing both x and y coordinates, which we use to determine the quadrant of a plane. When representing coordinates on a plane, we must first understand the position of points on a cartesian plane concerning the mathematical signs, which can be a+ or a-.
The Coordinates divide the cartesian plane into 4 quadrants using axes XX’ and YY’. Following are the 4 quadrants:
- The region XOY is called the 1st quadrant here; both X and Y are positive.
- The region X’OY is called the 2nd quadrant here; only X is positive and Y is negative.
- The region X’OY’ is called the 3rd quadrant here; X is negative and Y is positive.
- The region Y’OX is called the 4th quadrant here; both X and Y are negative.
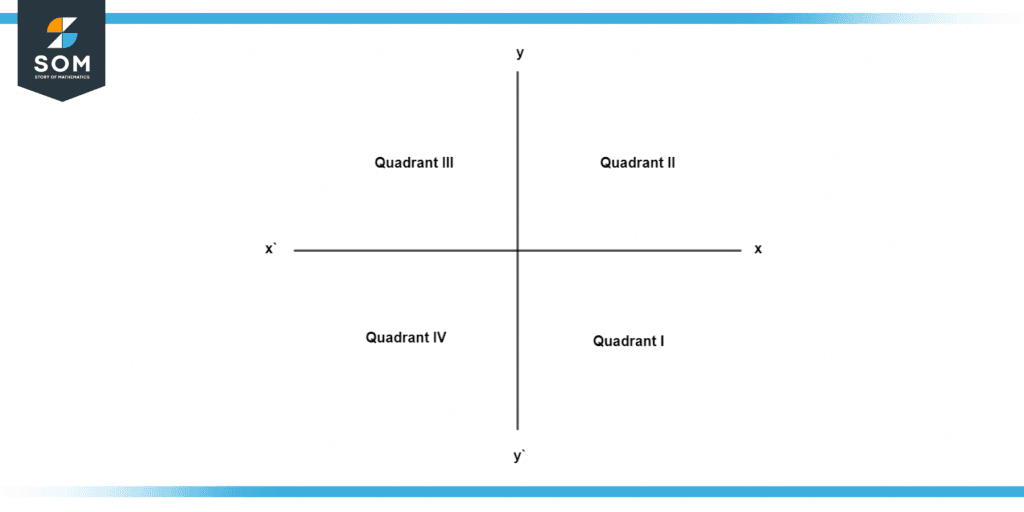
Figure 2 – Division of Quadrants in a Plane
Coordinates of a Point
A point, when plotted on a plane, uses an ordered pair consisting of values of both the x-axis and y-axis generally. To understand the concepts better, take a look at the following example:
In the following example, we can see that the following points have been plotted:
A = (2, 3)
B = (-4, 4)
C = (-2, -1)
D = (4, -2)
We can see that these points have been plotted by using both their x coordinates and y coordinates.
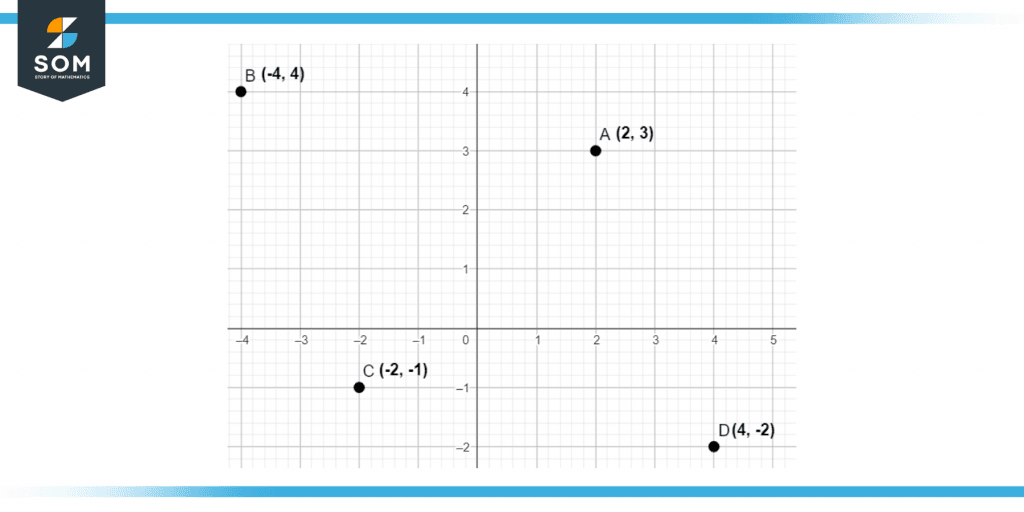
Figure 3 – Points plotted in a plane representing their coordinates
How To Read a Coordinate?
To plot a point, we must first know how to deal with a coordinate, and for that, we must be aware of certain points:
- To find the x coordinate, look at the perpendicular distance of the point from the y axis
- To find the y coordinate, find the perpendicular distance of the point from the x-axis
- After both of the coordinates have been found, write them in a round bracket which will be separated by a comma in this form (x, y)
- The first number, which represents the x-axis, is known as absicca
- The second number, which represents the y-axis, is called the ordinate
Uses of Coordinates
Coordinates hold significant importance in geometry and mathematics. They are used to perform different operations. Some of its uses are as below:
- The and y coordinates are used to find the slop of a line
- The x and y coordinates are used to find the distance between two points and the midpoint of a line
- The x and y coordinates help us in locating the exact position on the map
- The x and y coordinates are used to find the equation of a line
Types of Coordinates
If we go into the depth of coordinates, we get to know that 2 types of coordinate systems are used on a daily basis. Let us take a look at them.
Cartesian Coordinate System
It is a system that uses mutually perpendicular lines on a plane to denote the coordinates of a point. These lines may also b referred to as axes.
To locate a point, we can use these perpendicular lines, and the point where they both meet can be the desired point on the plane when we’re dealing with the x-axis and y-axis. The coordinates are referred to in the form of A(x, y), where x represents the number on the x-axis and y represents the y-axis.
Polar Coordinate System
It is a system where the origin, where both axes meet, holds quite important as it is taken as the reference point known as a pole. The pole is used to find the points depending on the distance of the point from the origin.
The coordinates are referred to in the form of (r,θ), where r represents the radius of the line and θ represents the angle which is forms between the line segment and the axis.
Coordinates on a 2D Plane
When we are dealing with a point on a plane of x-axis and y-axis, and the intersecting point is (0, 0), then it is known as a 2D plane, and any point plotted on such a plane consisting of perpendicular distances from both x and y axes will have 2D coordinates.
We write them as A(x, y), where x represents the values of the x-axis and y represents the values of the y-axis.
Coordinates on a 3D Plane
When we need to find a point in a 3D plane, we use the 3D coordinate system. This system consists of 3 axes; the x-axis, y-axis, and z-axis, which all are perpendicular at a single point known as the origin. We represent it in the following form: A(x, y, z)
Solved Examples of Coordinates
Example 1
If the centroid of a triangle has the following vertices (5, 2), (6,3), (8,2). Find the x and y coordinates.
Solution
The vertices of the triangle are: (5, 2), (6,3), (8,2)
(x1, y1) = (5, 2)
(x2, y2) = (6,3)
(x3, y3) = (8,2)
Coordinates = [(x1 + x2 + x3)/3, (y1 + y2 + y3)/3]
Putting values:
= [(5 + 6 + 8)/3, (2 + 3 + 2)/3]
= (19/3), (7/3)
= (6.3, 2.3)
Example 2
Harvey needs to find the x and y coordinates of the midpoint of a line with endpoints (-4, 4), (2, 8).
Solution
The points that we have are:
(x1, y1) = (-4, 4)
(x2, y2) = (2, 8)
To find the midpoints we will use the following formula:
MidPoint = [(x1 + x2)/2, (y1 + y2)/2]
= [(-4 + 2)/2, (4 + 8)/2]
= (-2/2, 12/2)
= (-1, 6)
Images/mathematical drawings were created with GeoGebra.
