JUMP TO TOPIC
Coplanar|Definition & Meaning
Definition
Co-planar refers to a collection of points, lines, line segments, rays, or other geometrical forms that all lie on the same plane.
In geometry, two terms share the same pronunciation and might be difficult to distinguish. Coplanar and co-linear describe them. “Co” means together, “linear” means “lying on a straight line,” and “planar” means “laying on a plane” in each of these phrases. Therefore, co-linear and coplanar are terms for objects that jointly lie on a line or a plane, respectively.
Coplanar Points
If there is a plane that encompasses both two lines in three dimensions, they are said to be coplanar. If the lines cross one another or are parallel, this happens. Skew lines are two lines that are not coplanar.
Four distinct points, x1, x2, x3, and x4 are coplanar if and only if their scalar triple product is equal to zero.
The set of points is said to be non-Coplanar points if these points are not in the plane. An example of Coplanar and non-coplanar points is illustrated in figure 1.
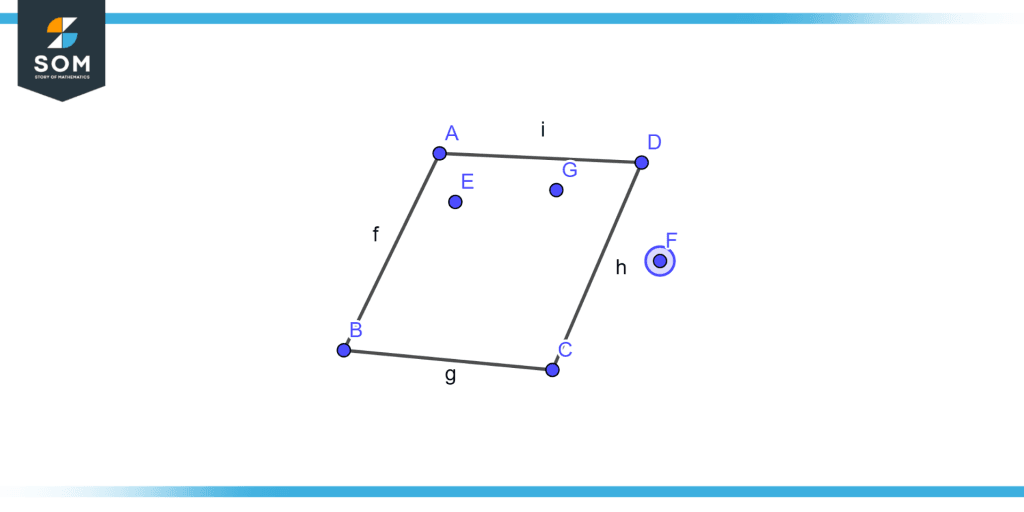
Figure 1 – Coplanar and non-coplanar points.
Points E and G are coplanar, while H is a non-coplanar point.
Coplanarity in N-dimensions
The challenge of establishing whether a group of points is coplanar is often only of importance when there are at least four points involved because three or fewer points are invariably coplanar. There are a variety of ad hoc ways that may be used when there are precisely four points. There is also a general method that we can apply to the case of any number of points, which makes use of vector methods and the fact that a plane is specified by two linearly independent vectors.
Coplanar and Non-coplanar Lines
If the lines lie on the same plane, they are coplanar lines, while the lines not on the plane are called non-coplanar lines. In figure 2, EF and GH are the coplanar lines, while IJ is the non-coplanar lines as illustrated below.
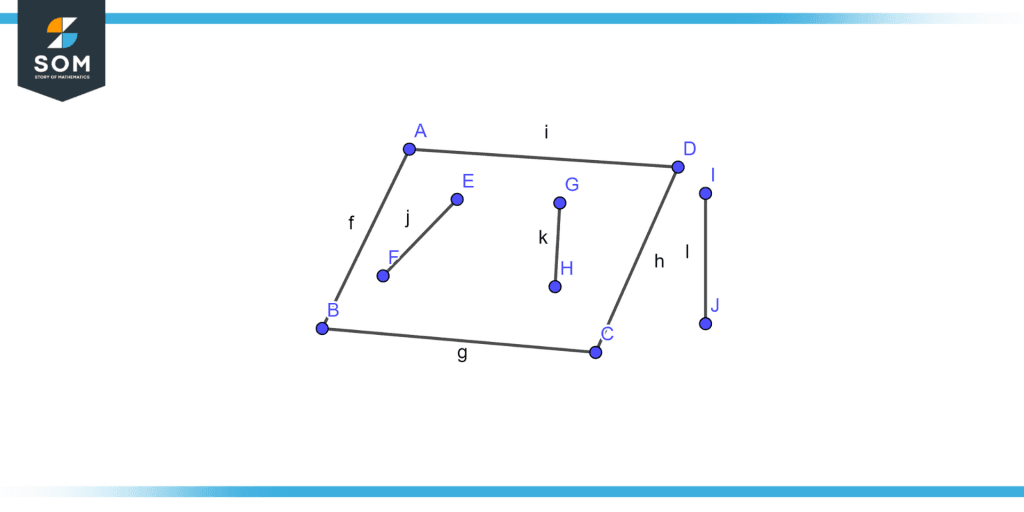
Figure 2 – Coplanar and non-coplanar lines.
Coplanar Vector
Coplanar vectors are those in a three-dimensional space that is located on the same plane. These are parallel vectors in the same plane. Any two random vectors may always be found that are coplanar in a plane.
Conditions for Coplanar Vector
Following are the conditions for vectors to be coplanar
- Three vectors in a three-dimensional space are coplanar only if the scalar triple product of the three vectors is zero.
- Three vectors in three-dimensional space, that are linearly independent of one another, are coplanar.
- In the situation of n vectors, all vectors are coplanar if there are no more than two linearly independent vectors.
Coplanar vectors are a type of mathematical structure that is frequently employed in the study of math, physics, engineering, and other subjects. Figure 3 illustrates the example of the coplanar vector.
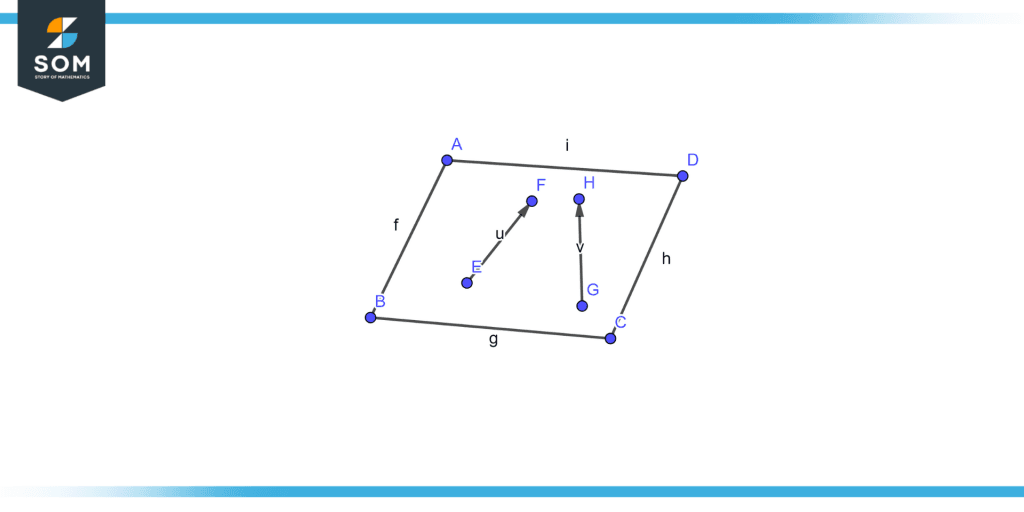
Figure 3 – Coplanar vectors.
Coplanar Forces
When forces occur simultaneously at the same place and in the same plane, they are referred to as concurrent forces rather than coplanar forces. Forces may be adjusted in a variety of ways. It is frequently simpler to deal with a sizable, complex system of forces by breaking it down into a smaller and smaller number of issues.
There are several ways to manipulate forces. In general, breaking down a large, complex system of forces into smaller and smaller difficulties makes it easier to manage. Coplanar systems of forces are easier to resolve than others.
The “resolution” of forces or force systems is what is meant by this. One method to make what would otherwise appear to be an impossibly complex system of forces operating on a body simpler is to do this. It is simpler to resolve some systems of forces than others. All the forces in a coplanar force system act on the same plane. They might be parallel, non-parallel, concurrent, or non-concurrent. Algebra or graphic statics can be used to solve any of these systems. Figure 4 illustrates the example of Concurrent and coplanar forces.
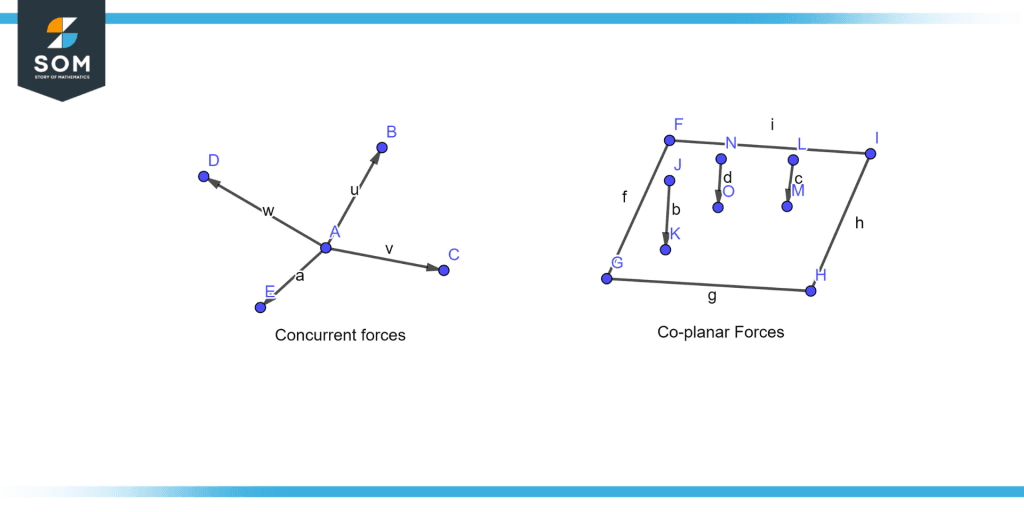
Figure 4 – Concurrent and coplanar forces.
Solved Examples Related to Coplanar Geometry
Example 1
Determine whether Points A, B, and C illustrated in figure 5 are coplanar.
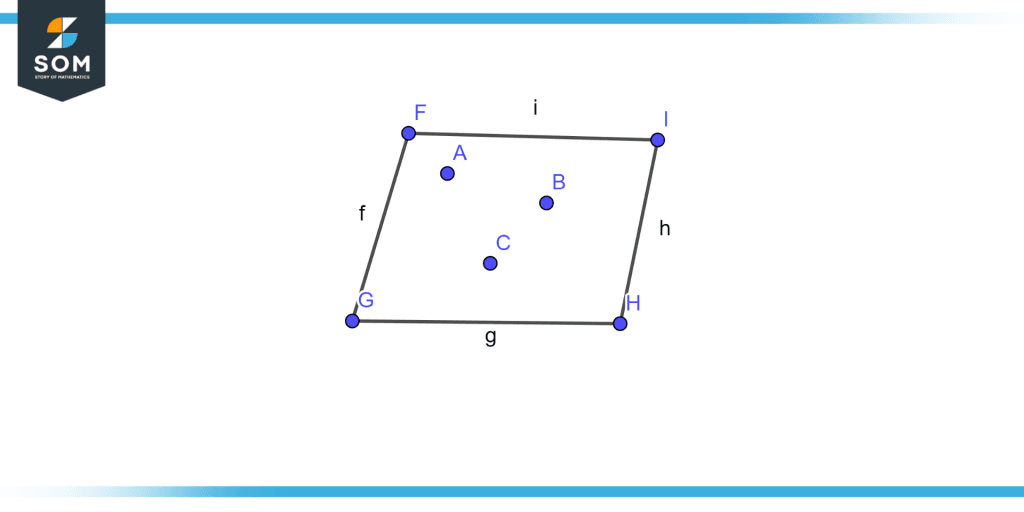
Figure 5 – Coplanar points.
Solution
Point A, B, and C lies in the same plane so these points are coplanar.
Example 2
Determine whether Points L, K, J, G, I, and H illustrated in figure 6 are coplanar.
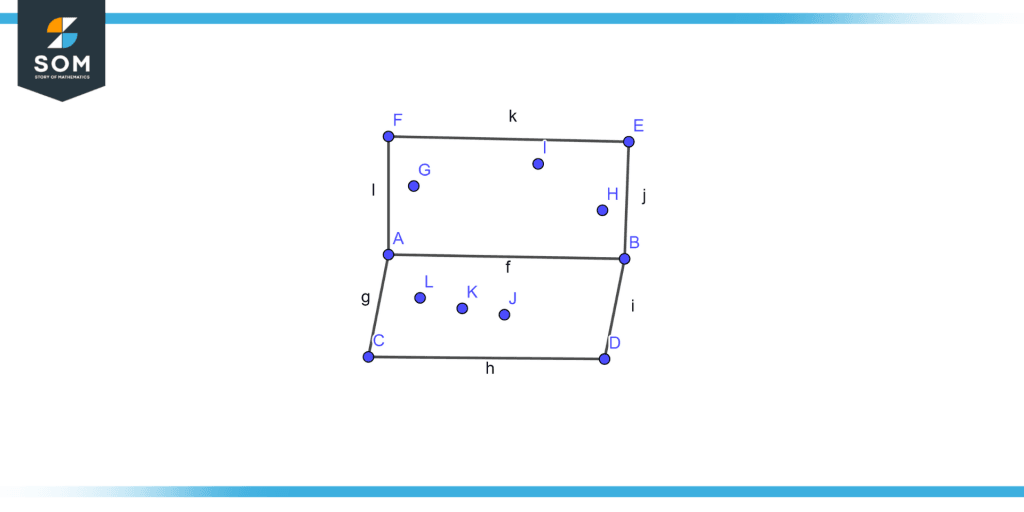
Figure 6 – Non-coplanar points.
Solution
Points L, k, and J are in plane ABCD while G, I, and H are in plane ABEF so these points are non-coplanar.
Example 3
Determine whether the given vectors are coplanar.
x = {1; 2; 3}
y = {1; 1; 1}
z = {1; 2; 1}
Solution
To evaluate whether the vectors are coplanar or not, we have to evaluate the scalar triple product
x . [y × z] = (1)·(1)·(1) + (1)·(1)·(2) + (1)·(2)·(3) – (1)·(1)·(3) – (1)·(1)·(2) – (1)·(1)·(2)
=1+2+6-3-2-2
=2
As the scalar triple product is equal to 2 so the given vectors are not coplanar.
Example 4
Determine whether the given vectors are coplanar.
x = {1; 1; 1}
y = {1; 3; 1}
z = {2; 2; 2}
Solution
To evaluate whether the vectors are coplanar or not, we have to evaluate the scalar triple product
x . [y × z] = (1)·(2)·(3) + (1)·(1)·(2) + (1)·(1)·(2) – (1)·(2)·(3) – (1)·(1)·(2) – (1)·(1)·(2)
=6+2+2-6-2-2
=0
As the scalar triple product is equal to zero so the given vectors are coplanar.
Example 5
A cube is illustrated in figure 8 to determine whether the following points are coplanar or not
a) A, B, and D
b) A, B, and G
c) E, F, G, B, and D
d) E, F, B, and A
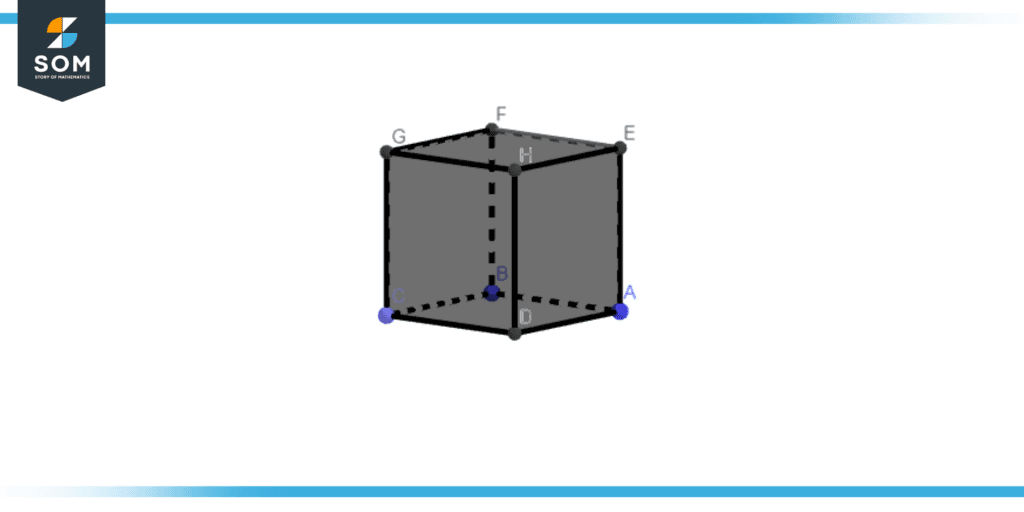
Figure 7 – Coplanar and non-coplanar points in a cube.
Solution
a) Points A, B, and D lie on the same plane so these are coplanar points.
b) Points A and B lie on the same plane while point G lie on the other plane so these points are not coplanar
c) Points E, F, and G lie on the same plane while points B and D lie on the other plane so these points are not coplanar.
d) Points E, F, B, and A lie on the same plane so these are coplanar points.
All images/mathematical drawings were created with GeoGebra.
