JUMP TO TOPIC
Cosine Rule|Definition & Meaning
Definition
The cosine rule, often known as the law of cosines, is used to solve triangles. It states: “The sum of the squares of the lengths of any pair of sides of a triangle minus two times the product of these two sides’ lengths multiplied by the cosine of the angle between them equals the square of the side length opposite to this angle.”
Figure 1 shows a triangle PQR. The length of the triangle’s three sides are p, q, and r, and their corresponding angles are P, Q, and R.
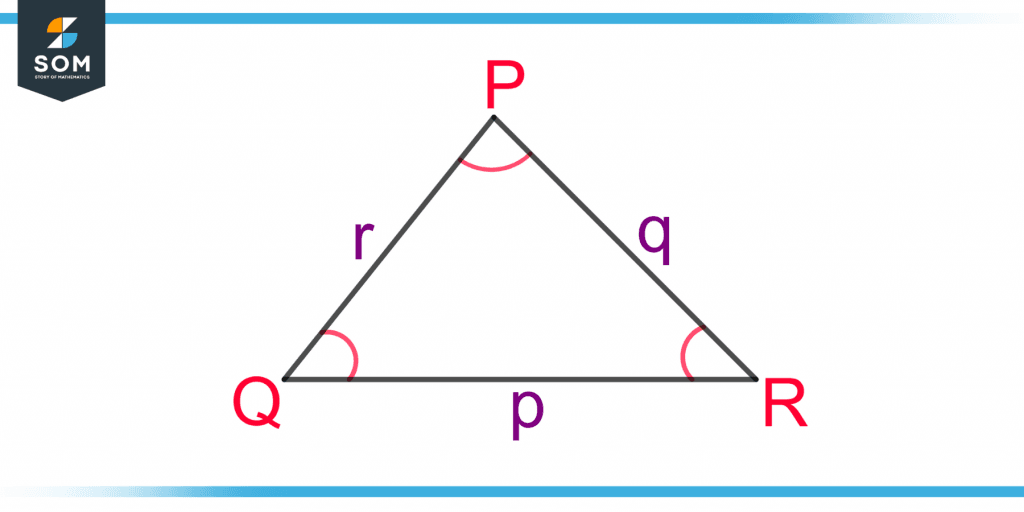
Figure 1 – A Triangle PQR for the Demonstration of the Cosine Rule
The cosine rule for the side r is given as:
r2 = p2 + q2 – 2pq.cos(R)
For the same figure, the other two forms of cosine rule are:
p2 = q2 + r2 – 2qr.cos(P)
q2 = p2 + r2 – 2pr.cos(Q)
Concept of Opposite Side
The side opposite to any given angle is termed the opposite side or the side opposite to that angle. Its concept is always associated with an interior angle of a triangle and is essential while dealing with the cosine rule. Figure 2 shows a triangle with three interior angles: L, M, and N.
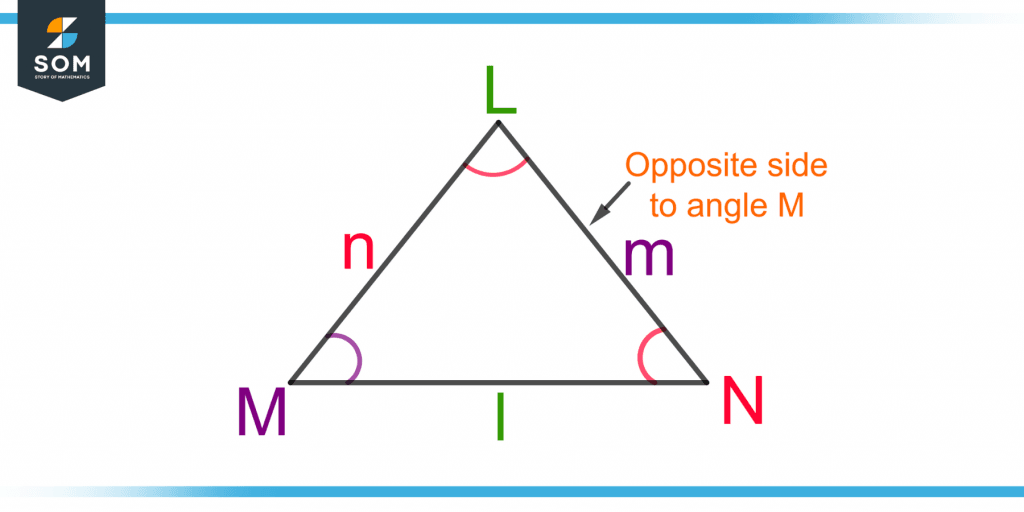
Figure 2 – Demonstration of the Opposite Side in Triangle LMN
The side opposite to angle L is l. Similarly, the side opposite to angle M is m, and the side opposite to angle N is n.
Solving a Triangle
A triangle is a polygon with three angles, three sides or edges, and three vertices. It is a two-dimensional closed shape in which no diagonal can be drawn. The cosine rule is used to solve the following types of triangles.
SAS Triangle
A SAS triangle refers to a Side-Angle-Side triangle, which means two adjacent sides and the angle between them. The cosine rule solves a triangle in which the factors known are the two adjacent sides and their corresponding angle to find the third side opposite to the given angle.
SSS Triangle
A SSS triangle refers to a Side-Side-Side triangle. The three sides are given, and the three angles are unknown. The three angles can be calculated using the three forms of the cosine rule to solve the triangle.
Sum of Angles of a Triangle
The sum of the angles of a triangle equals 180°. If the three angles of the triangle are P, Q, and R, their sum can be written as:
P + Q + R = 180°
It is used to calculate the third angle if the two angles of the triangle are known.
Pythagoras Theorem
The Pythagoras theorem only applies to right-angle triangles, whereas the cosine rule applies to all triangles, so it generalizes the Pythagoras theorem. Figure 3 shows a right-angle triangle UVW.
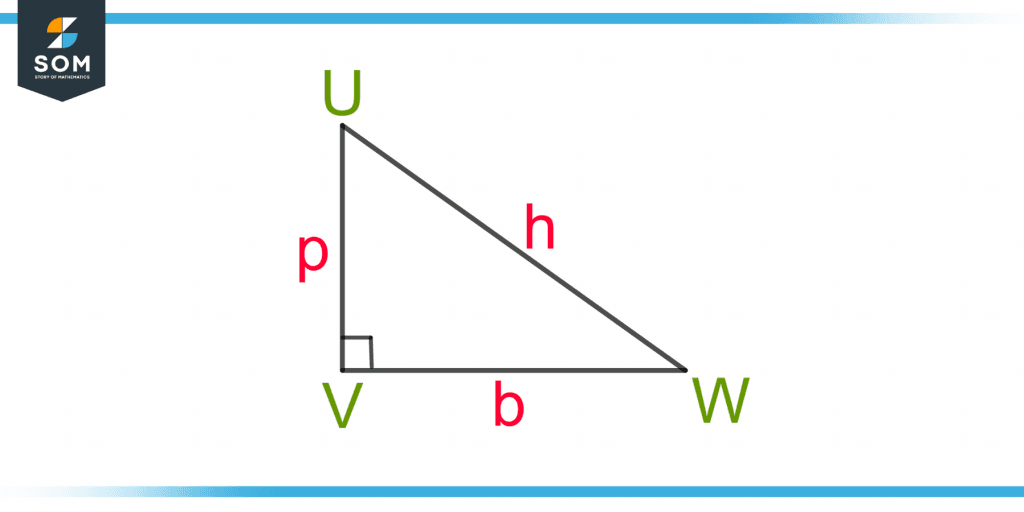
Figure 3 – A Right-angle Triangle UVW with Hypotenuse(h), Base(b), and Perpendicular(p)
The side opposite to the perpendicular (90°) angle is the longest side, known as the hypotenuse h. The base b is the side adjacent to the right angle, and the perpendicular p is the height of the triangle. The Pythagoras theorem is given as:
h2 = p2 + b2
The cosine rule is given as:
r2 = p2 + q2 – 2pq.cos(R)
If the angle R is taken as 90°, then the triangle is a right-angle triangle. Putting the value in the cosine rule gives:
r2 = p2 + q2 – 2pq.cos(90°)
As:
cos(90°) = 0
So:
r2 = p2 + q2
Which is the same as the Pythagorean theorem.
Derivation of Cosine Rule
Figure 4 shows a triangle PQR. A perpendicular PM is drawn from vertex P to meet the side QR at point M.
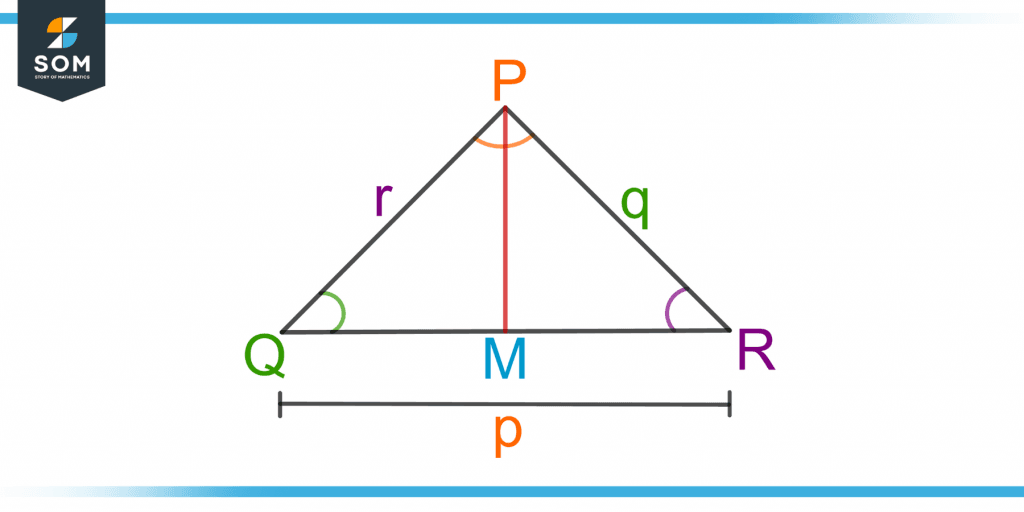
Figure 4 – A Triangle PQR with a Perpendicular PM drawn from Point P to meet the Side QR
In triangle PQM:
cos Q = QM / r
QM = r.cos Q
Similarly, in triangle PMR:
cos R = RM / q
RM = q.cos R
In triangle PMR, the Pythagoras theorem is given as:
PR2 = PM2 + RM2
Also, RM can be written as:
PR2 = PM2 + (QR – QM)2
Expanding the above equation gives:
PR2 = PM2 + QR2 + QM2 – 2.QR.QM
Also:
PM2 + QM2 = PQ2
Replacing (PM2 + QM2) with PQ2 in the above equation:
PR2 = PQ2 + QR2 – 2.QR.QM
As we know from figure 4:
QR = p, PR = q, PQ = r, QM = r.cos Q
Replacing PR, PQ, QR, and QM in the above equation gives:
q2 = r2 + p2 – 2.p.(r.cos Q)
which is the cosine rule and is the same as:
q2 = p2 + r2 – 2pr.cos Q
Rearranging the above equation gives:
cos Q = (p2 + r2 – q2) / 2pr
Similarly, we can also prove the other forms of the cosine rule.
Examples
Example 1 – SAS Triangle
A triangle PQR is shown in figure 5. Find the length of the third side using the cosine rule.
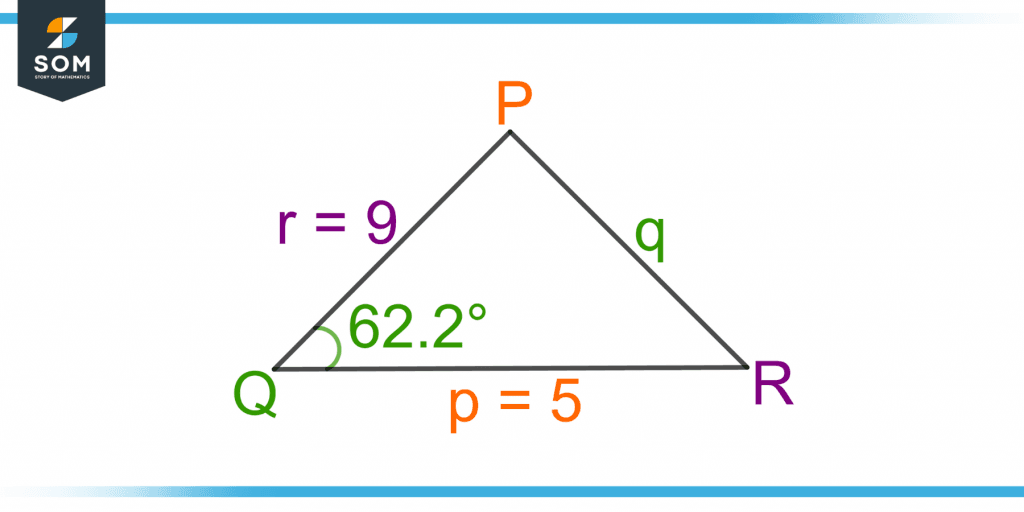
Figure 5 – A Triangle PQR with the Parameters given as the SAS Triangle
Solution
The length of two adjacent sides, p and r are given as 5 and 9, respectively. The angle between sides p and r is 62.2°. The cosine rule for side q is given as:
q2 = p2 + r2 – 2pr.cos(Q)
Here,
p = 5, r = 9, Q = 62.2°
Putting the values in the above equation gives:
q2 = (5)2 + (9)2 – 2(5)(9).cos(62.2°)
q2 = 25 + 81 – 42
q2 = 64
q = 8
Hence, the length of the side opposite to angle Q is 8.
Example 2 – SSS Triangle
Figure 6 shows a triangle PQR. Find the three angles of the triangle.
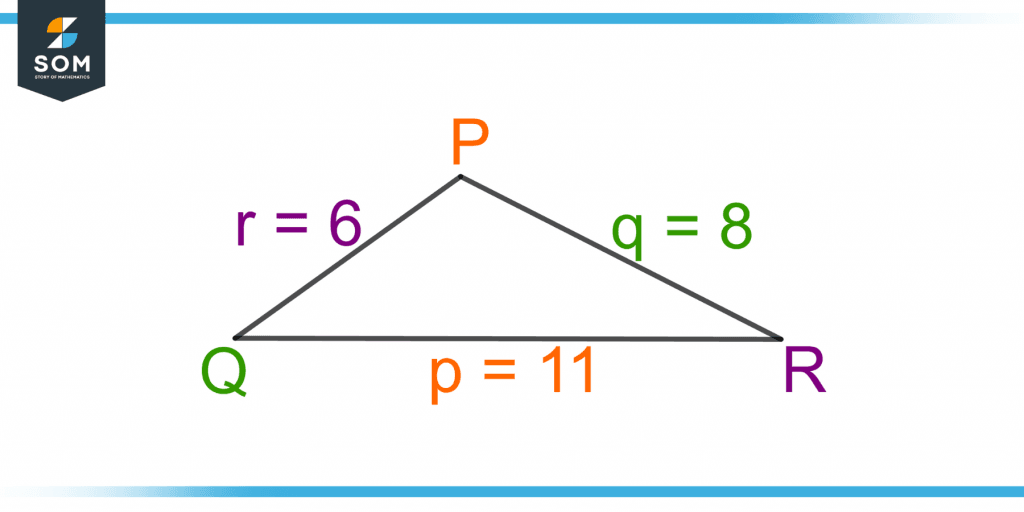
Figure 6 – A Triangle PQR with the Parameters given as the SSS Triangle
Solution
The length of the triangle’s three sides, p, q, and r, is given as 11, 8, and 6. Using the cosine rule for angle P as:
p2 = q2 + r2 – 2qr.cos(P)
Rearranging the above equation gives:
cos(P) = (q2 + r2 – p2) / 2qr
Here:
p = 11, q = 8, r = 6
Putting the values gives:
cos(P) = [(8)2 + (6)2 – (11)2] / 2(8)(6)
cos(P) = [64 + 36 – 121] / 96
cos(P) = – 21 / 96
cos(P) = – 0.21875
P = 102.6°
Using the cosine rule for angle Q as:
cos Q = (p2 + r2 – q2) / 2pr
Putting the values of p, q, and r gives:
cos Q = [(11)2 + (6)2 – (8)2] / 2(11)(6)
cos Q = [121 + 36 – 64] / 2(11)(6)
cos Q = [121 + 36 – 64] / 132
cos Q = 93 / 132
cos Q = 0.7045
Q = 45.2°
As the sum of three angles of a triangle is 180°, so:
P + Q + R = 180°
For the angle R, rearranging the equation gives:
R = 180° – P – Q
Putting the values of P and Q gives:
R = 180° – 102.6° – 45.2°
R = 32.2°
All the images are created using Geogebra.
