Density|Definition & Meaning

The mathematical definition of density is very straight forward but the concept is very critical and important when we are dealing with quantity of matter. Density plays an important roles in many mathematical and scientific applications. It is the property of the material. This means that every material has a fixed density depending upon its internal structure. For example the density of iron and aluminum is 7800 and 2700 kilogram per cubic meters respectively.

Given the density information and the dimensions (or volume) of the material, we can easily find the mass by using the definition of density. This is explained in detail later in this article. This article covers a comprehensive introduction to the concept of density and its mathematical concepts. It also introduces some examples. 

Explanation of Density

Lets consider an example as shown in the figure below.

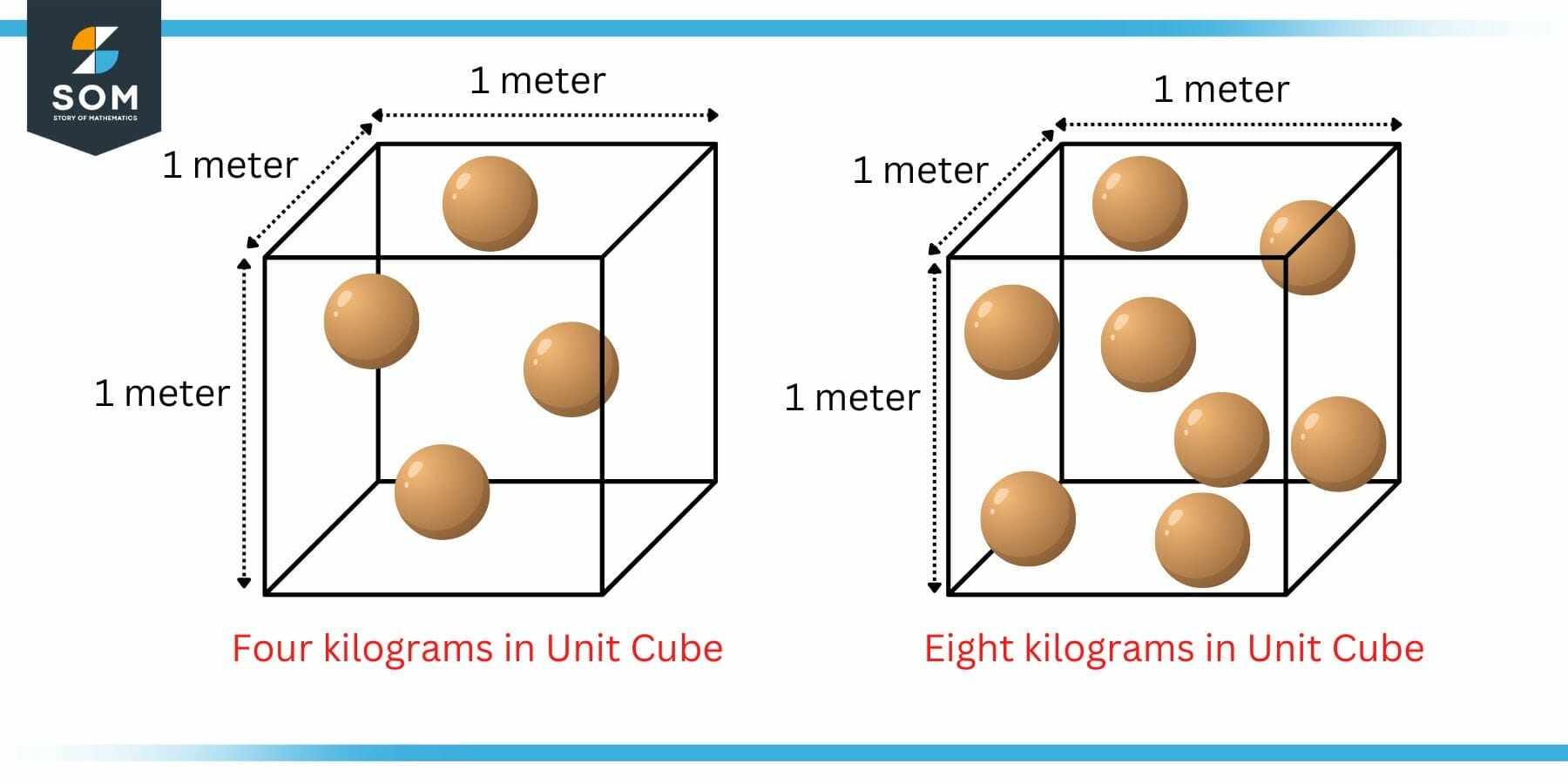
Figure 1: Unit Cube Example of Density

The above figure shows two boxes. Each box has fixed dimensions of 1 meter x 1 meter x 1 meter. In other words its a unit cube. The spheres inside the box represent one kilogram of matter each.

Now from mathematical definition, in the left box, there are four spheres packed in a unit cube which means that there are four kilograms packed in a unit cube. We can say that the density of this cube is four kilogram per cubic meter.

In the right box, there are eight spheres packed in a unit cube which means that there are eight kilograms packed in a unit cube. We can say that the density of this cube is eight kilogram per cubic meter.

Mathematical Form of Density

The above example was very intuitive and limited to unit cube for developing some basic understanding. This section introduces the concept of density in a more mathematically formal way.

Lets say that you are given with a piece of volume ‘V’ of some material that has density ‘d’. If ‘m’ kilograms of the matter are packed inside the given volume ‘V’, then the relationship between these quantity is formulated as follows:

d = $\mathsf{\dfrac{ m }{ V }}$

In SI units, the density ‘d’ is measured in ‘kilogram per cubic meter’, ‘m’ is measured in ‘kilogram’ and ‘V’ is measured in ‘cubic meter’.

The above formula can also be described as, “The mass of material per unit volume is called density“. This formula can be used in solving the numerical problems involving density.

Lets consider the similar example of figure 1 with a different arbitrary volume of the cube as shown in the figure 2.

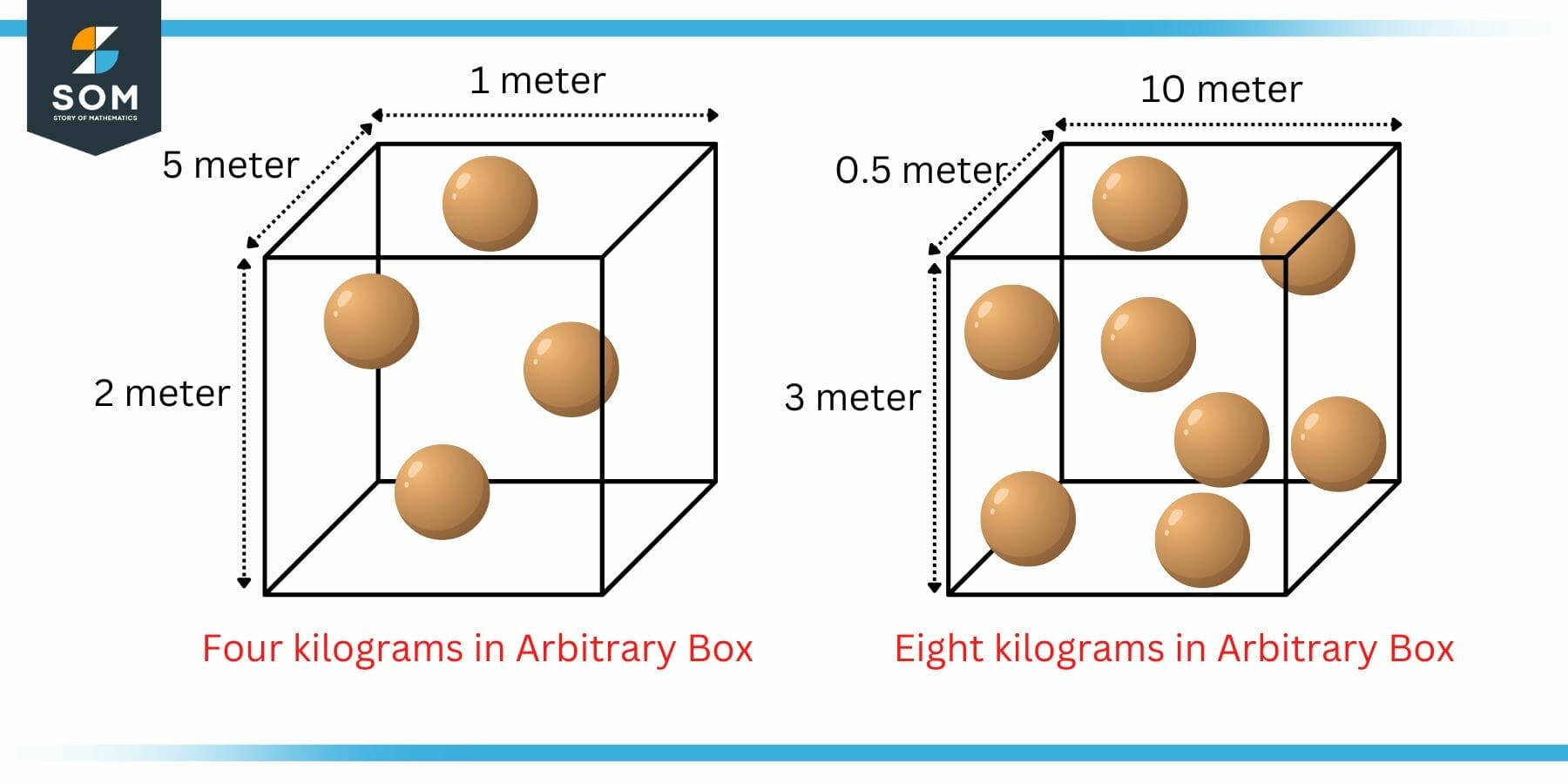
Figure 2: Example of Density with Arbitrary Cube Size

In the left box, the density can be using the above formula. Here, the volume is 2 meter x 5 meter x 1 meter which is equal to 10 cubic meters. As stated earlier, there are four kilograms of matter packed inside this 10 cubic meters volume. Mathematically:

d = $\mathsf{\dfrac{ m }{ V }}$ = $\mathsf{\dfrac{ 4 }{ 10 }}$ = 0.4 kg/m³

In the right box, the volume is 3 meter x 0.5 meter x 10 meter which is equal to 15 cubic meters. As stated earlier, there are eight kilograms of matter packed inside this 15 cubic meters volume. Mathematically:

d = $\mathsf{\dfrac{ m }{ V }}$ = $\mathsf{\dfrac{ 8 }{ 15 }}$ = 0.533 kg/m³

Examples of Density

The concept of density can be extended to many real life situations. Consider the case of population density for example. We have often heard that a particular area is densely populated while the other is sparsely populated. This is dependent on the value of the density (relative density to be specific).

Following figure illustrates this point. Two areas are shown in the figure. The left one is sparsely populated while the one on the right is densely populated. This decision is made on the basis of the density. The density of right one is higher than the left one since it contains more people in the same space compared to the left park.

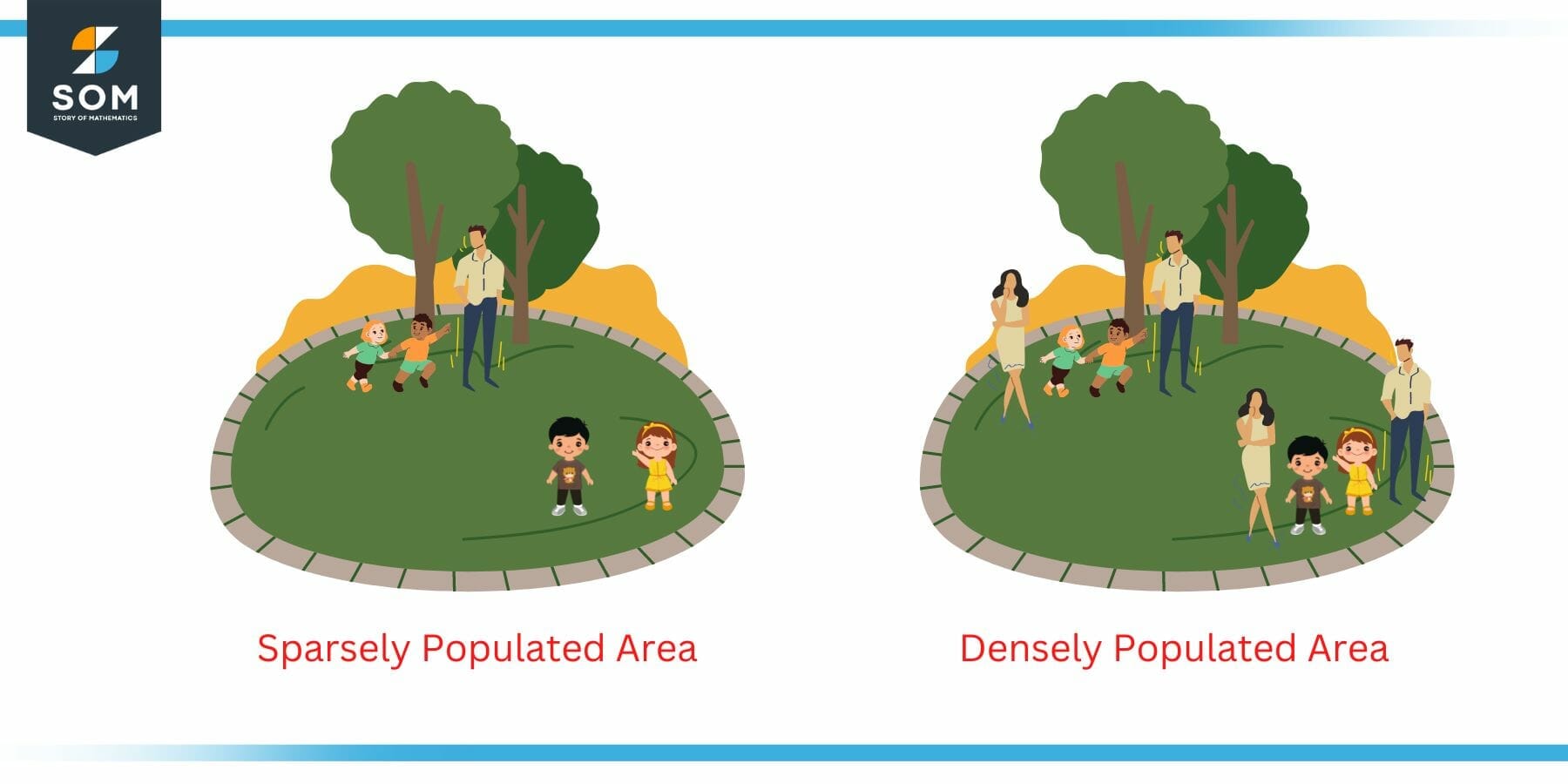
Figure 3: Example of Population Density

Density as a Measure of Heaviness

The density of a body can be used as a measure of heaviness. Lets say that someone asks you to pick up a two blocks of same size. One of the block is made of some heavy metal say iron while the other is made of some light metal say aluminum.

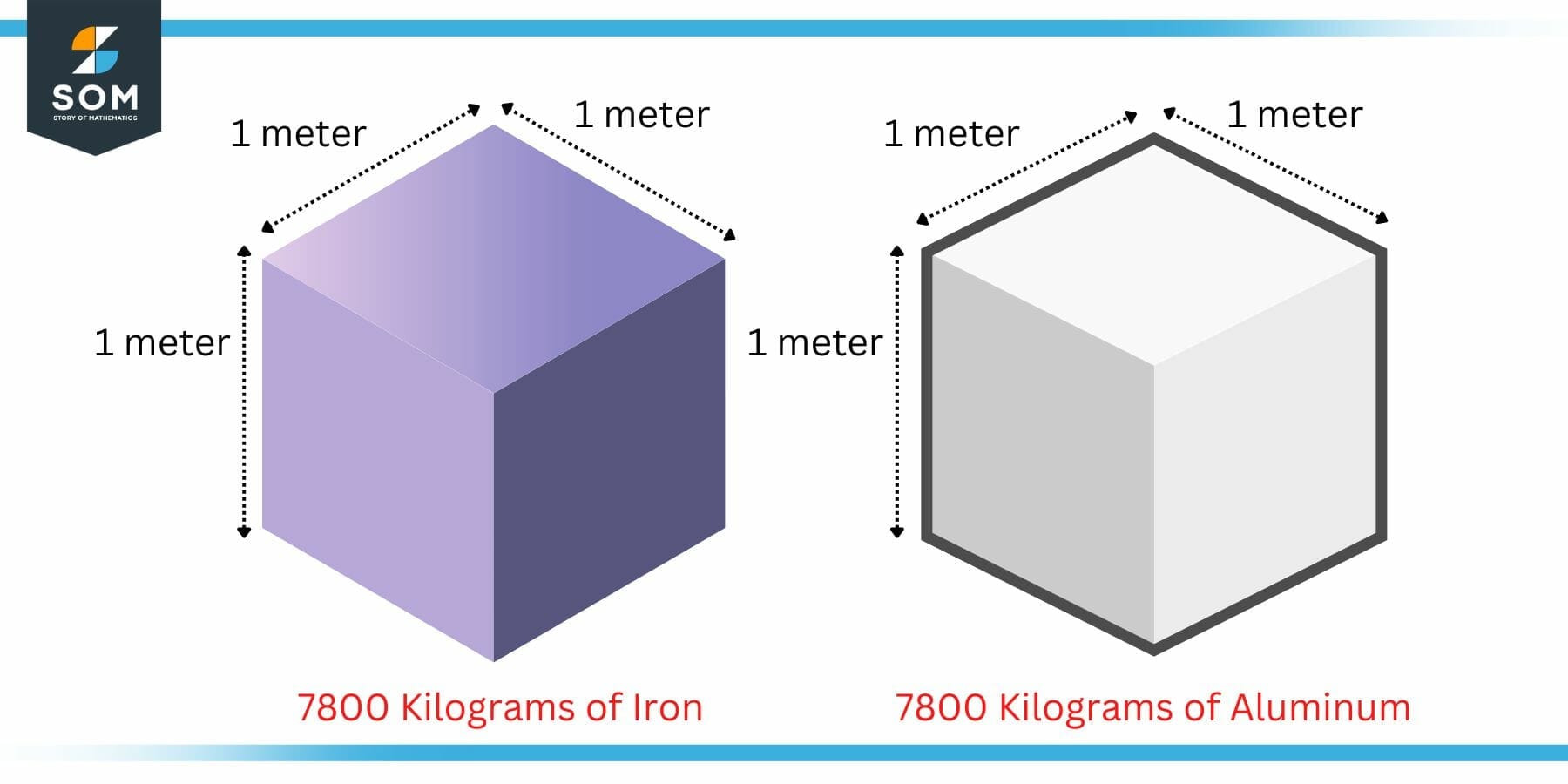
Figure 4: Example of Density as a Measure of Heaviness

Now we know from our experience that the iron block will be heavy compared to the aluminum one. However, the mathematical explanation may be found in the density. The density of iron is 7800 kilogram per cubic meter while that of aluminum is 2700 kilogram per cubic meter.

Since the density of iron is higher, it will have more matter in the same size volume. Hence, the iron block is heavier.

Numerical Problems of Density

Example 1

An iron block has a width of 2 meters, height of 1 meters and depth of 0.5 meters. If the mass of the 7800 kilograms, find the value of its density.

Solution

Given that:

m = 7800 kilogram

V = 2 meters x 1 meter x 0.5 meters = 1 cubic meter

Recall:

d = $\mathsf{\dfrac{ m }{ V }}$

Substituting values:

d = $\mathsf{\dfrac{ 7800 \textsf{ kilogram} }{ 1 \textsf{ cubic meter} }}$

d = 7800 kilogram per cubic meter

Example 2

An aluminum block has a width of 4 meters, height of 0.5 meters and depth of 0.25 meters. If the density of the aluminum is 2700 kilograms per cubic meters, find the value of its mass.

Solution

Given that:

d = 2700 kilogram per cubic meter

V = 4 meters x 0.5 meters x 0.25 meters = 0.5 cubic meter

Recall:

d = $\mathsf{\dfrac{ m }{ V }}$

Substituting values:

2700 kilogram per cubic meter = $\mathsf{\dfrac{ m }{ 0.5 \textsf{ cubic meter} }}$

Rearranging:

m = (2700 kilogram per cubic meter) x (0.5 cubic meter)

m = 1350 kilogram

All images/mathematical drawings were created with GeoGebra.

Denominator Definition < Glossary Index > Deposit Definition