Division|Definition & Meaning

Concept Building

Dividing simply means making equal parts or dividing into equal amounts among a group. An equal-area triangle consists of two equal triangles divided by a diagonal in a square. Depending on the division operation, the result may be an integer or not. Decimal numbers may sometimes be used to represent the result.

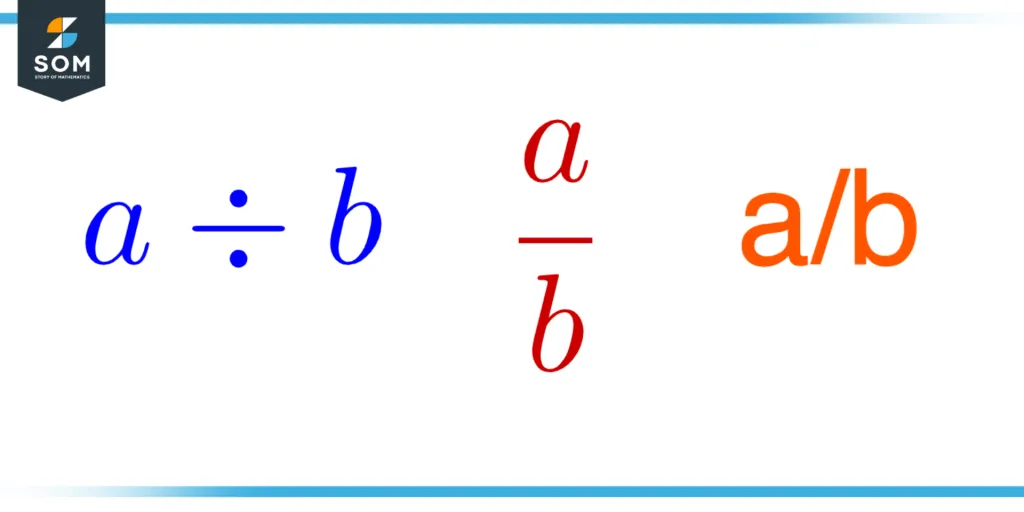
Figure 1 – Symbol of Division

Let us take an example of division. There are 50 students and 5 classes; we want to divide the students among the 5 classes. What we will do is simply split the students into 5 batches of 10 students each, and send each batch to a separate class. Thus, we have assigned 50 students equally in 5 classes, with each class containing 10 students. 

We can consider division as a repetition process of successive subtraction or the opposite of the multiplication operation.

Symbol Representation

There are generally three different symbols used for division shown above

Divide ($\boldsymbol\div$)

Division of number 6 with 3 gives:

6 $\div$ 3 = 2

Forward Slash ($\boldsymbol/$)

Division of 4 books among 2 students:

4/2 = 2

Bar ($\boldsymbol{\frac{\phantom{a}}{\phantom{b}}}$)

Division of 8 apples among 4 people:

$\mathsf{\dfrac{8}{4}}$ = 2

Mathematical Formula for Division

$\mathsf{\dfrac{Dividend}{Divisor}}$ = Quotient + Remainder

Dividend

The dividend is the term or item which we want to split into different equal sub-parts. For example, if we want to divide 10 oranges among 5 people then the 10 oranges will be the dividend.

Divisor

The divisor is the term that split the dividend into equal sub-parts or in other words we can say the term with which we want to divide something. In the above example, 5 people are the divisor.

Quotient

The result obtained by the splitting of the two items is known as the quotient, for example dividing 10 oranges among 5 people gives a quotient of 2. In other words, the quotient is the term that decides the quantity of each subgroup.

Remainder

The remainder is the residual result left after the division operation for example division of 10 pencils among 3 students results in the remainder equal to 1.

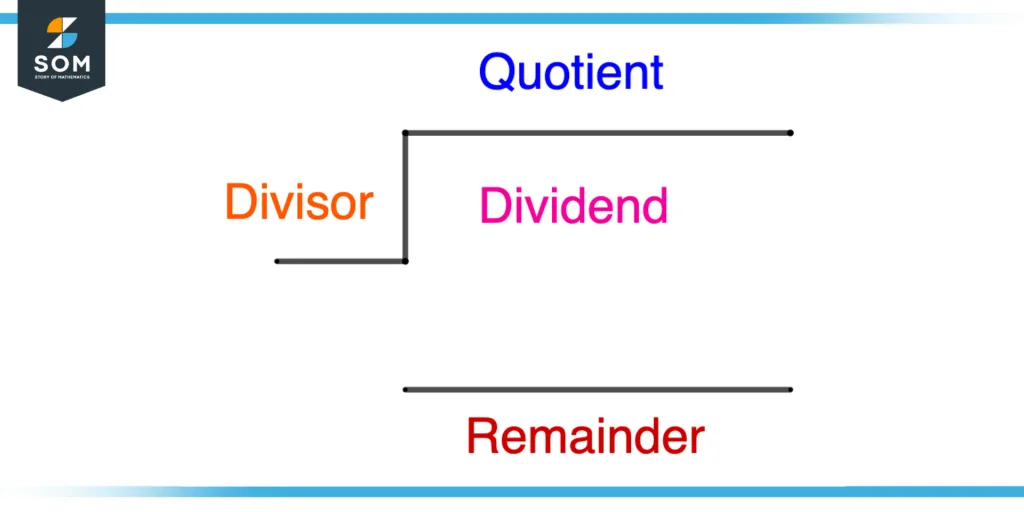
Figure 2 – Parts of Division Formula

Order of Division Operation

In mathematics, Division is highly prioritized among other arithmetic operations. Division operation has the first-order meaning that whenever there is an arithmetic problem we will first perform division operation.

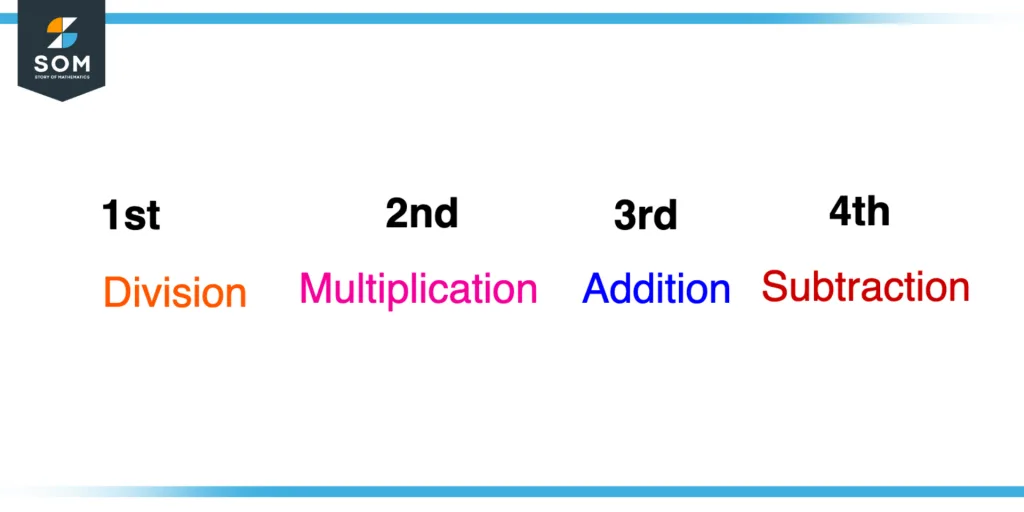
Figure 3 – Order of Division Operation

Properties of Division

1. The division of any number by integer 1 gives the number itself or in other words division of any number gives the dividend as the result.
2. The division of any number by integer 0 gives infinity or more precisely not defined.
3. The division of a number by the number itself gives the result as 1 or in other words, if the dividend and divisor are the same then the result will be equal to 1.
4. If the dividend is 0 then the division operation with any other number gives 0.
5. If we divide any number by 100 the remainder will be equal to the number at the unit and tens position and the rest of the number will be considered quotient.

Dividing Fractions

It is possible to divide fractions as well. Division operators need to be transformed into multiplication operators when dividing fractions. The following example shows the concept.

\[ \mathsf{ \frac{4}{3} \div \frac{4}{2} = \frac{4}{3} \times \frac{2}{4} = \frac{2}{3} } \]

In fraction, the division sign is changed into a multiply sign with the fraction being reversed as shown.

Dividing Float Numbers

Mathematics consists of a variety of concepts that divide decimal numbers. In many ways, the decimal division is similar to the fractional division. To understand how decimal division works, let’s look at the example below.

4.5 $\div$ 2.5 = $\mathsf{ \dfrac{45}{25} }$ = $\mathsf{\dfrac{9}{5}}$ = 1.8

Dividing Polynomials

It is possible to divide polynomials by other polynomials, as opposed to numbers and fractions. Two methods are available for polynomial division, however. As opposed to dividing numbers, the polynomial long division uses polynomial expressions to divide polynomial expressions. The synthetic division method is another way to divide polynomials.

Steps for Division

1. First, figure out the data and define terms such as divisor and dividend.
2. Write the dividend inside the division symbol hat as shown below example.
3. Write the divisor outside the hat of the division symbol as shown below example.
4. Now start dividing the dividend by the divisor and write the result on the top of the hat.
5. This result written on the top will be considered as the quotient.
6. If the dividend is not completely divided then bring the next digit down and repeat the process.
7. On repeating the process if we got any residual result left at the end and further dividend cant be divided then we will consider this residual result as the remainder.

Examples of Division

Example 1

Consider a scenario there are 51 players, and we want to make n teams in such a way that each team consists of players not more or less than 3. Describe the division process graphically also. How many numbers of teams can be formed?

Solution

As from the problem statement, we are provided with the dividend as 51 players and divisor as 3, so in order to find the n teams that can be formed, we will simply divide 51 by 3, which gives us 17. So we can make 17 teams by splitting or dividing 51 players into teams of 3 players each. The calculation is shown below.

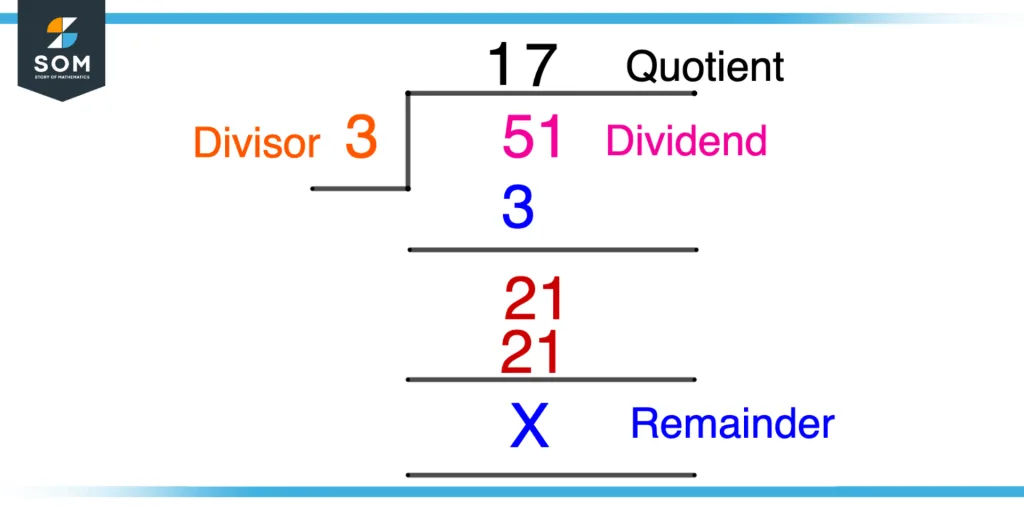
Figure 4 – Division of Players Examples

Example 2

Harry bought 16 Oranges, 4 Bananas, and 20 Apples for his family. The number of count of his family member is 4, including him. How will you divide all the fruits among family members of Harry?

Solution

We illustrate the division process in figure 5 below.

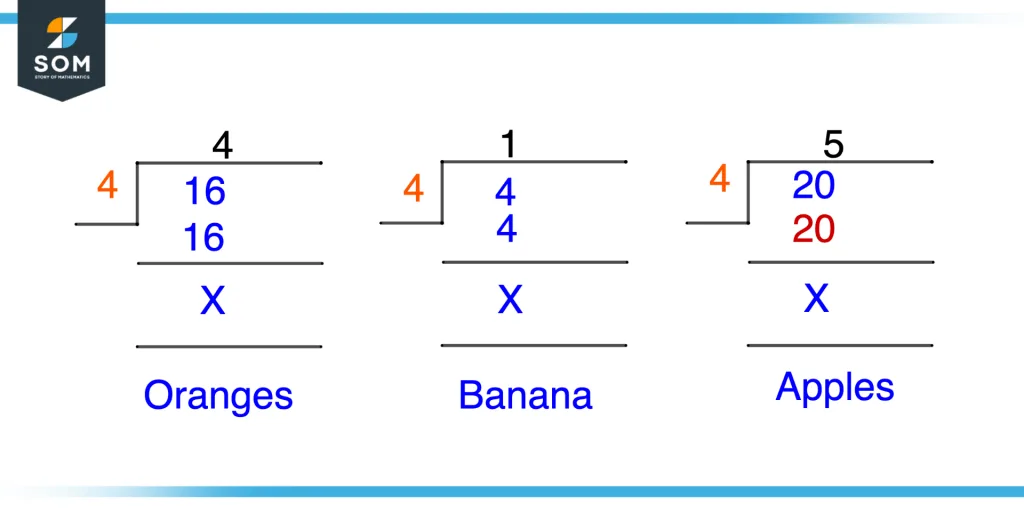
Figure 5 – Division of Fruits Example

Division of Oranges

Total oranges = 16

Number of family members = 4

Dividend = 16

Divisor = 4

Solving (leftmost in figure 5), we get:

Quotient = 4

Division of Bananas

Total bananas = 4

Number of family members = 4

Dividend = 4

Divisor = 4

Solving (middle in figure 5), we get:

Quotient = 1

Division of Apples

Total apples = 20

Number of family members = 4

Dividend = 20

Divisor = 4

Solving (rightmost in figure 5), we get:

Quotient = 5

So each family member got 4 oranges, 1 banana, and 5 apples.

All mathematical drawings and images were created with GeoGebra.

Divisible Definition < Glossary Index > Domain Of A Function Definition