Domain of a Function|Definition & Meaning

After we enter an x value, the process outputs this sequence of values. 

\[ f: X \rightarrow Y \]

Figure 1 below illustrates the domain of a function.

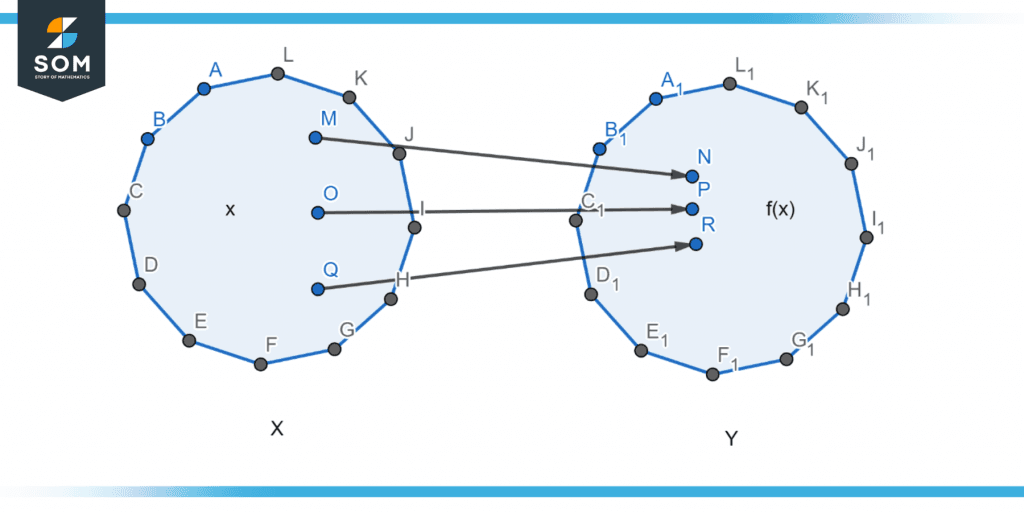
Figure 1 – Representation of a domain function.

Explaining Domains

A domain is the specified input of any function. You may claim that “domain” or “limited domain” is “man-made.” It is positioned by the question or by a component of the question that came before it that sets a constraint.

To be more exact, in $f: X \rightarrow Y$, the range of f is X given a function. In contemporary mathematical terminology, a function’s domain is a component of its definition rather than a quality. The function f could be plotted in the cartesian grid in the specific situation where X and Y are subsets of R. In this instance, the domain is shown on the graph’s x-axis as the reflection of the function’s graph onto the x-axis.

The set of values actually obtained by a function $f: X\rightarrow Y$ (a fraction of Y) is referred to as its range or image, while the set of all values obtainable by the function is referred to as the co-domain. The co-domain of a function is hence a superset of the its range.

A function may also be considered a “map” from inputs to outputs. For instance, the arrows in the picture below depict how the input (here on the left) is translated into the target value (on the right). Even though this graphic appears to be “unmathematical,” it accurately depicts a function. A portion of any function’s domain may be constrained.

What Are Co-domains?

A function’s co-domain is the collection of all feasible outputs. It is designated by domain and is referred to as the domain of a function f (f). The set among all potential output values is the function’s range: 

$\text{range}(f)=\left \{ f(x):x \ \in \ \text{domain}(f)  \right \}$

Nevertheless, the range refers to the outputs which are used. The domain in the picture above is 1, 3, and 4, whereas the co-domain is 3, 6, 8, and 9. The only numbers in the range that contains arrowheads are 3, 6, and 9. You will often work with the range instead of the co-domain.

Figure 2 below shows a simple function that displays input as domain-to-output as co-domain mappings as arrows.

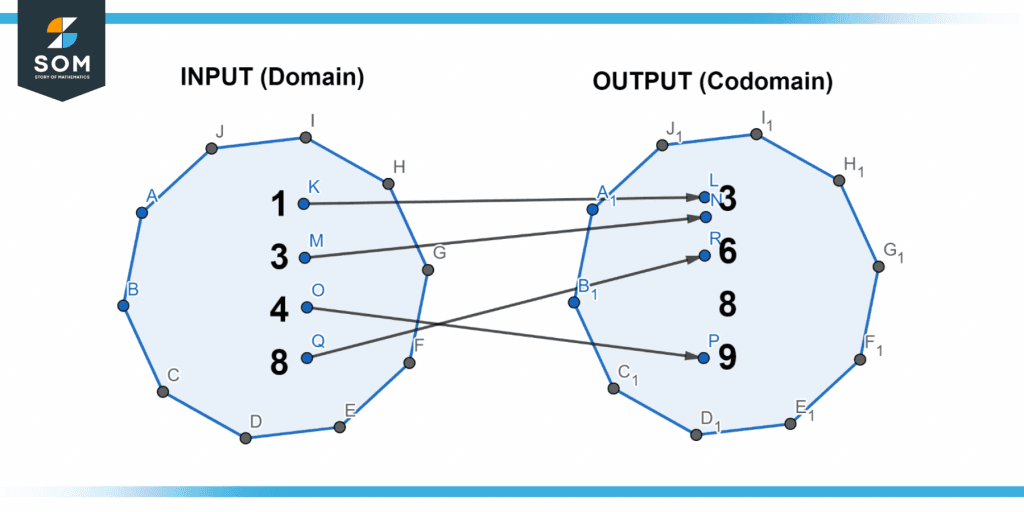
Figure 2 – Representing co-domain of a function.

Explaining Natural Domain

A natural domain is an area where that specific function is defined. Its natural domain is the longest chain of domains under which a function may be analyzed and extended to a single-valued variable. 

If a formula specifies a real function, f, it may not be defined for all possible values. In this situation, the set of actual figures on which the equation may be converted to an actual number is known as the natural range or range of interpretation of f. An incomplete function is frequently referred to as just a function, and its natural range is referred to as just a domain.

Rules of Finding the Domain of a Function

• The set containing all real numbers makes up the function f(a) domain.
• In the set including all real numbers except for zero, $f(a) = \frac{1}{a}$.
• If the collection includes all real numbers where $a\geq 0$ exists, then $f(a)=\sqrt{a}$.
• The set contains all real numbers such that a > 0 is the domain; hence, $f(a)=ln (a)$.

Domain as Square Root Function

A value y such that $y^{2}=x$, or a variable y whose square is equal to x, is the sum of squares of a value x in mathematics.

The primary square root, also known as the non-negative square root, of any non-negative real integer x, is represented by the symbol $\sqrt{x}$, where sqrt is also known as the radical sign or radix. For instance, we say $ \sqrt{9} = 3$ to indicate that the main square root of the 9 is 3. The radicand is the phrase (or integer) whose square root has been analyzed. 

The number or phrase that appears under the radical symbol, in this example 9, is known as the radicand. The primary square root can alternatively be expressed in exponent notation for non-negative x as $x^{\frac{1}{2}}$.

Figure 3 shows a graph showing the non-negative real numbers that make up the domain of the genuine square root function $f(x)=\sqrt{x}$.

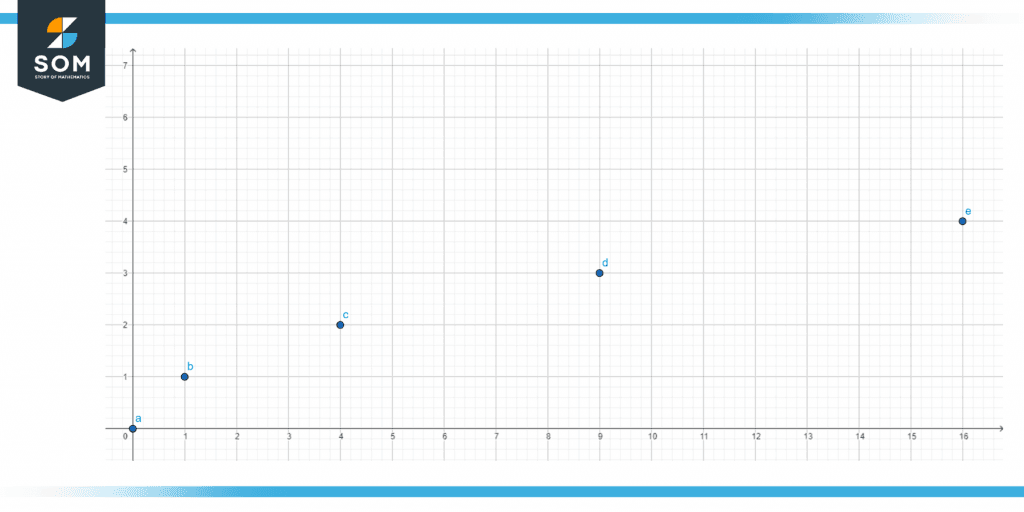
Figure 3 – Representation of a domain with square root function.

The Domain of Trigonometric Functions

In trigonometric functions, the angle of the right-angled triangle may be linked to side length ratios. Using real-world trigonometric functions, the right-angled triangle’s angle may be related to side length ratios.

Table 1 shows the domains of trigonometric functions.

Table 1 – Representation of domains in trigonometric functions.

Examples of Domain

Here are some of the examples of domains listed below

Example 1

Find the domain of a function  y = 2 – $ \mathsf{\sqrt{-4x + 2} }$

Solution

Only if the value included in a square root calculation is a non-negative value is a function defined. hence, take into account -4x + 2 $\geq$ 0.

Subtracting 2 on both sides: -4x $\geq$ -2 

Now, dividing both sides by 4: -x $\geq$ -0.5 $\Rightarrow$ x $\leq$ 0.5

Thus, the function’s domain is x $\leq  $ 0.5.

Example 2

Find the domain of a function y = 2 – $\mathsf{ \sqrt{-5x + 2}} $

Solution

Only if the value included in a square root calculation is a non-negative value is a function defined. hence, take into account -5x + 2 $\geq$ 0.

Subtracting 2 on both sides: -5x $\geq$ -2

Now, dividing both sides by 5 shows that the domain is x $\leq \frac{2}{5} $.

Example 3

Find the domain of a function y = 2 – $\mathsf{ \sqrt{-4x + 4}} $

Solution

Only if the value included in a square root calculation is a non-negative value is a function defined. hence, consider -4x + 4 $\geq$ 0.

Subtracting 4 on both sides: -4x $\geq$ -4.

Now, dividing both sides by 4 gets us the domain as x $\leq $ 1.

All images/tables are made using GeoGebra.

Division Definition < Glossary Index > Dot Plot Definition