Fahrenheit|Definition & Meaning

There are many scales of measuring temperature that have been in use in different parts of the world during different timelines. However, three units are most commonly used today. These include Celsius, Fahrenheit, and Kelvin scales. The following figure shows these scales side by side. 

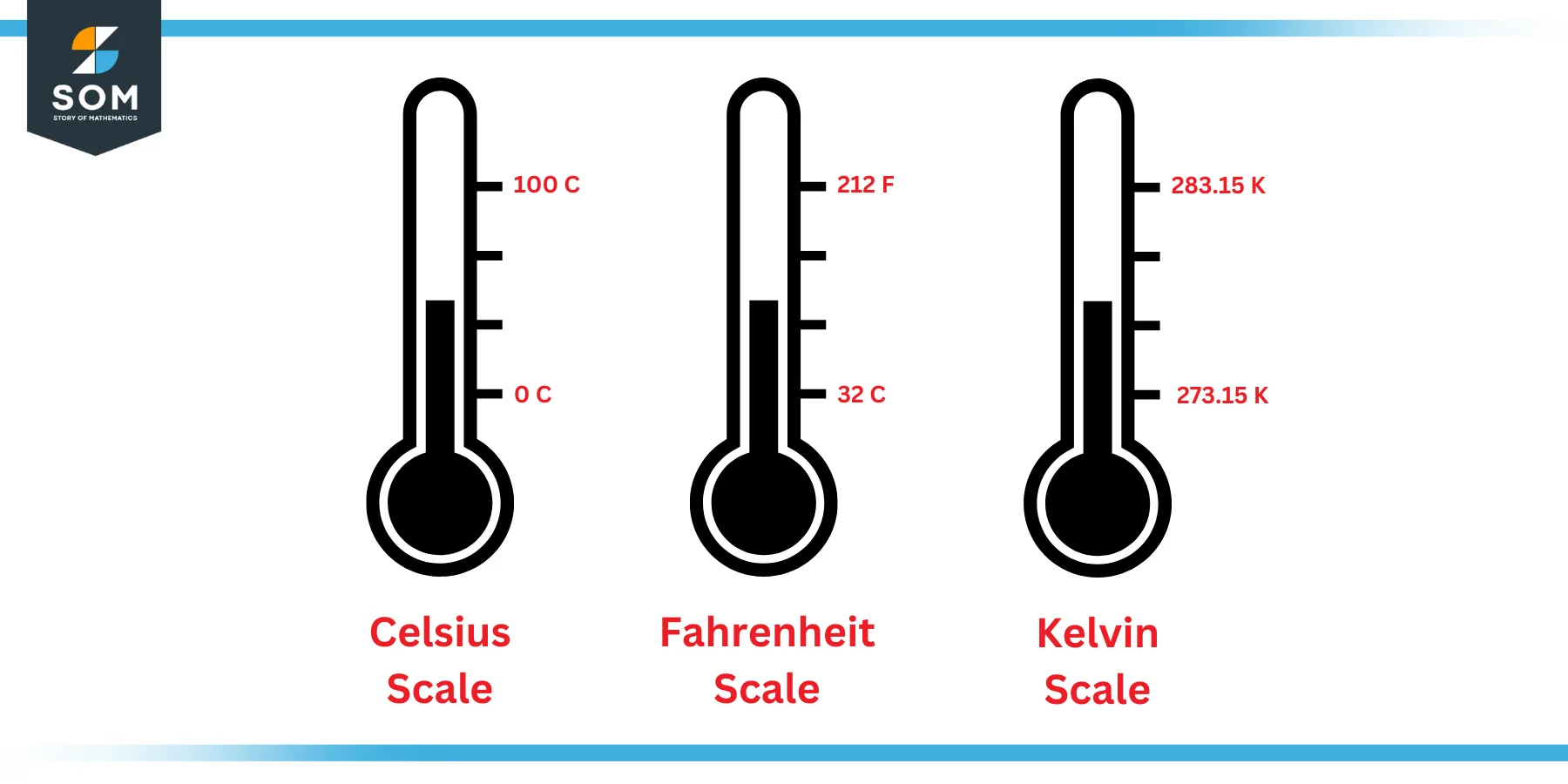
Figure 1: Celsius, Fahrenheit and Kelvin scales

As shown in the figure above, all three scales are related to each other through the freezing and boiling point of water. Consequently, all three scales are linear, and they can be completely defined by these two points.

The water freezes at zero degree Celsius, thirty-two degrees Fahrenheit and two hundred seventy-three Kelvin. It boils at a hundred degrees Celsius, two hundred and twelve degrees Fahrenheit and three hundred and seventy-three Kelvin.

Explanation of Fahrenheit Scale

All three of these scales have their own significance and utilization in terms of applications. While Celsius is used worldwide and Kelvin is the system international unit of temperature, Fahrenheit is the unit of choice when it comes to United States.

This scale is named after the renowned Polish physicist Daniel Gabriel Fahrenheit who invented the first ever precision thermometers in the seventeenth century. The scale is symbolized by capital letter F. Following figure shows some important temperature readings on this scale.

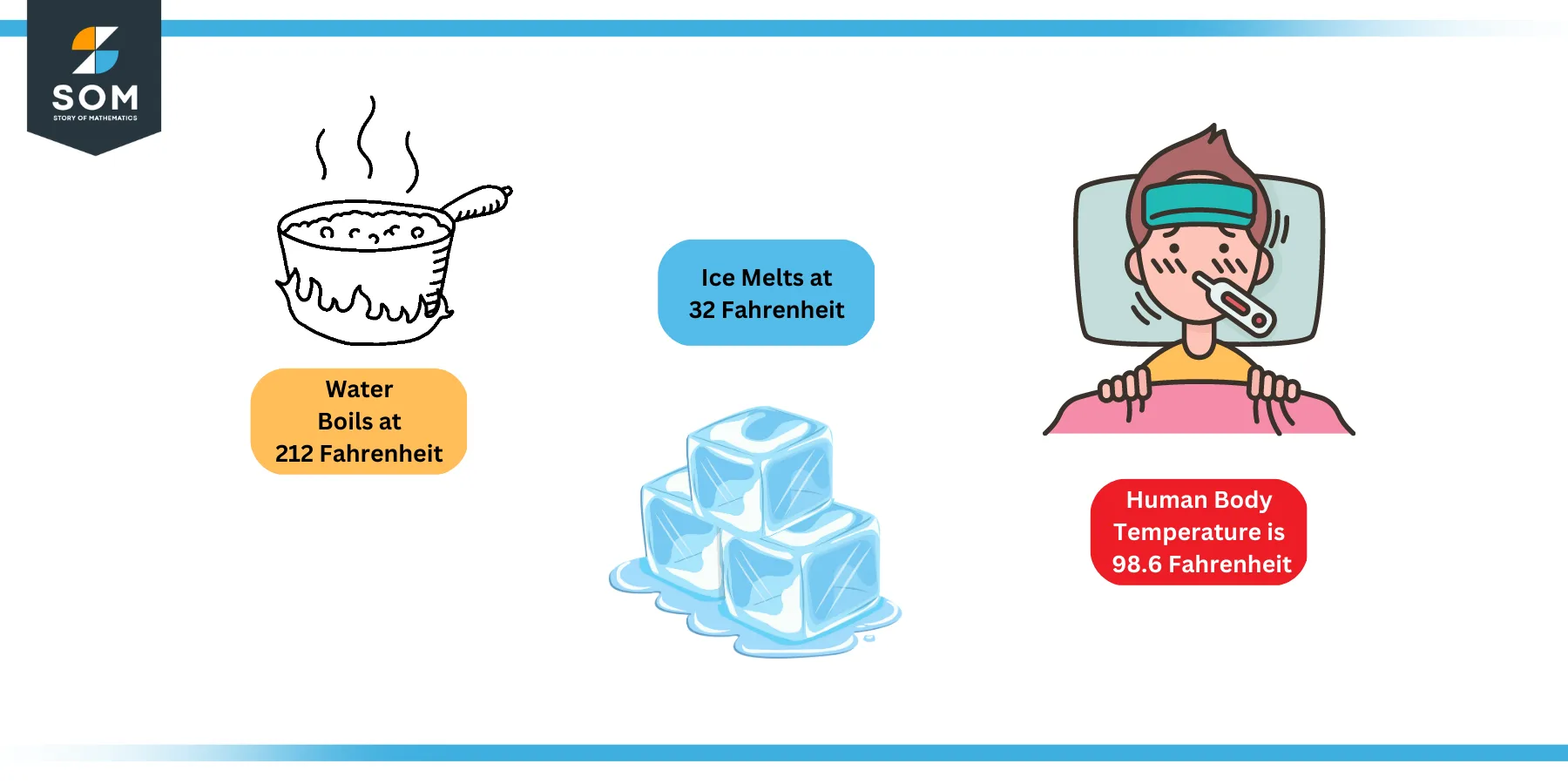
Figure 2: Important Temperature Readings on Fahrenheit Scale

Fahrenheit scale is the scale of choice in the medical community. Commonly used thermometer that we use for our body temperature to measure the fever is also graded in Fahrenheit scale. The normal human body temperature is 98.6 degree Fahrenheit.

The wide use of the Fahrenheit scale in the USA and the resistance to the adoption of the Kelvin or Celsius scale do have some logical reasons. One of the key reason is that the Fahrenheit scale is more suitable and intuitive in describing the outdoor temperature compared to the other scales.

It can be noticed that in many parts of the habitable world, the temperature does fall below zero degrees Celsius whereas in Fahrenheit, most areas are covered.

Similarly, on a hot summer day, the temperature is around a hundred degrees Fahrenheit in the USA. Therefore, the adoption of Fahrenheit is more suitable. The zero mark on this scale represents cold days of winter, while the 100-degree mark represents hot summer days.

Another notable reason for the use of Fahrenheit is that the resolution of the scale is larger than Celsius. Therefore more precise measurements can be noted on the Fahrenheit scale compared with Celsius or Kelvin.

Inter-conversion of Temperature Scales

Since all three scales of temperature are used in mostly all parts of the world, it is worthwhile to learn the interconversion formulae for these scales. As students of mathematics and science, we come across many such situations where an instrument measures in one scale of temperature while our formulae require the other one.

Or, there may be a situation when a scientist from one part of the world has to share temperature data with other scientists in other parts of the globe. So it is important to understand how these scales are related mathematically. The following headings summarize these interconversions.

Inter-conversion Between Fahrenheit and Celsius Scales

As explained earlier, both scales are linear, and the relationship can be drawn based on the temperature values of any two physical phenomena. Since we know the freezing and boiling points of water in both scales, we can formulate an equation of the line as follows:

F = 1.8 C + 32 … … … … (1)

The following figure explains this relationship:

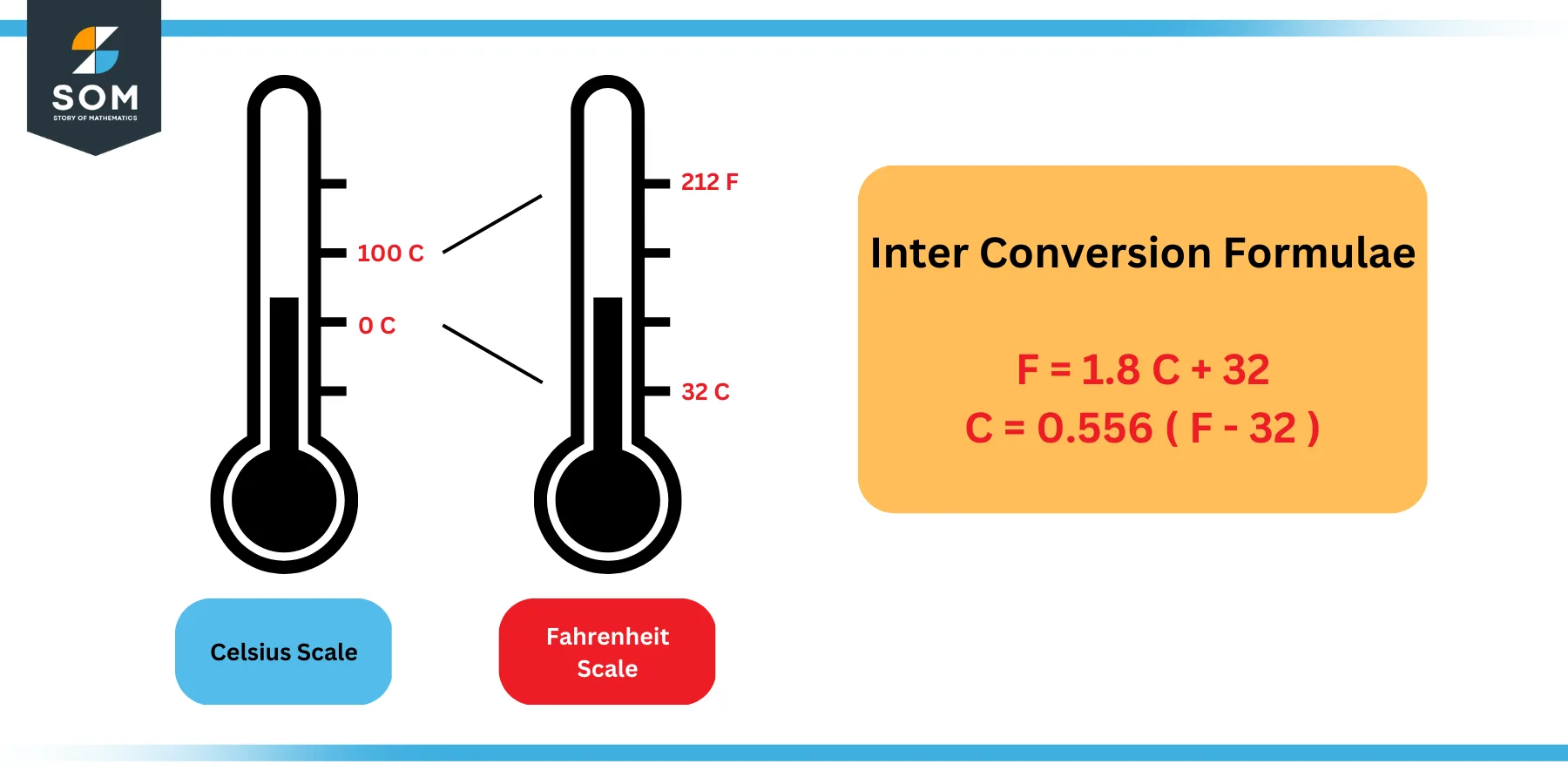
Figure 3: Inter-conversion between Fahrenheit and Celsius Scales

Which can be re-arranged to obtain the following formula:

C = 0.556 ( F – 32 ) … … … … (2)

Inter-conversion Between Fahrenheit and Kelvin Scales

Since we know the freezing and boiling points of water in both scales, we can formulate an equation of the line as follows:

F = 1.8 ( K – 273.15 ) + 32 … … … … (3)

The following figure explains this relationship:

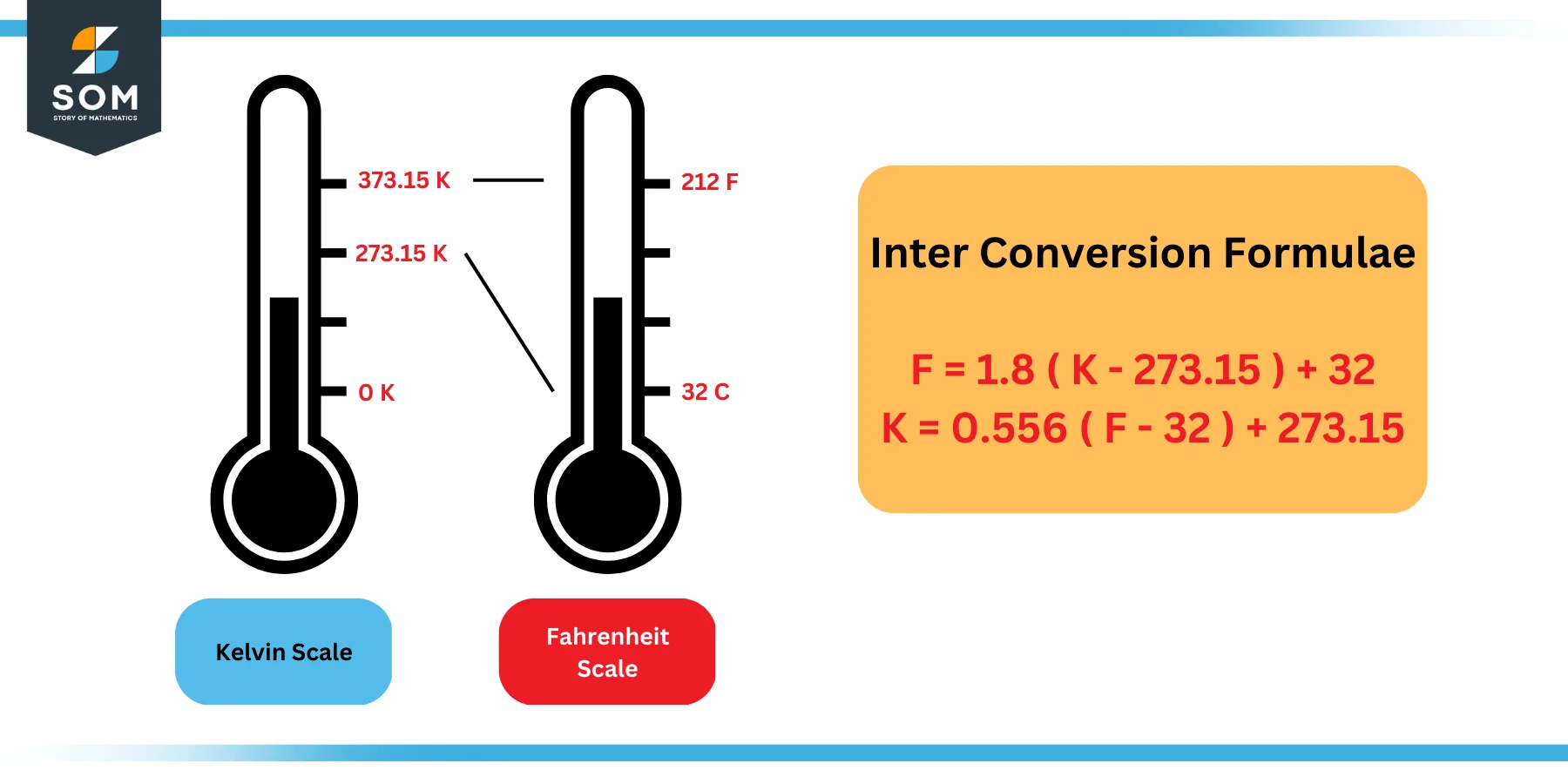
Figure 4: Inter-conversion between Fahrenheit and Kelvin Scales

Which can be re-arranged to obtain the following formula:

K = 0.556 ( F – 32 ) + 273.15 … … … … (4)

Examples of Inter-conversion

Since temperature conversion is a very commonly seen problem in real life as well as in many scientific problems, let us consider some numerical examples.

(a) Conversion from Celsius to Fahrenheit Scale

A can of water is heated up to a temperature of 80 degrees Celsius. Find the value of temperature in Fahrenheit scale. Using the formula no. 1 above:

F = 1.8 ( 80 ) + 32 = 176 degree Fahrenheit

(a) Conversion from Fahrenheit to Celsius Scale

A piece of ice is cooled to a temperature of 10 degrees Fahrenheit. Find the value of temperature in the Celsius scale. Using the formula no. 2 above:

C = 0.556 ( 20 – 32 ) = -6.67 degree Celsius

(a) Conversion from Kelvin to Fahrenheit Scale

The boiling point of a certain alcohol is 350 Kelvin. Find the value of temperature in Fahrenheit scale. Using the formula no. 3 above:

F = 1.8 ( 350 – 273.15 ) + 170.33 degree Fahrenheit

(a) Conversion from Fahrenheit to Kelvin Scale

The melting point of iron is 2800 degrees Fahrenheit. Find the value of temperature in the Kelvin scale. Using the formula no. 4 above:

K = 0.556 ( 2800 – 32 ) + 273.15 = 1812.158 Kelvin

Numerical Problems Involving Fahrenheit Temperatures

Part (a): Convert 70 degree Celsius to Fahrenheit

Part (b): Convert 200 degree Fahrenheit to Celsius

Part (c): Convert 273.15 Kelvin to Fahrenheit

Part (d): Convert 1000 Fahrenheit to Kelvin

Solution Part (a)

F = 1.8 C + 32

F = 1.8 ( 70 ) + 32

F = 158 degrees Fahrenheit

Solution Part (b)

C = 0.556 ( F – 32 )

C = 0.556 ( 200 – 32 )

C = 93.33 degree Celsius

Solution Part (c)

F = 1.8 ( K – 273.15 ) + 32

F = 1.8 ( 273.15 – 273.15 ) + 32

F = 32 degrees Fahrenheit

Solution Part (d)

K = 0.556 ( F – 32 ) + 273.15

K = 0.556 ( 1000 – 32 ) + 273.15

C = 810.93 degrees Celsius

All images/mathematical drawings were created with GeoGebra.

Factorising Definition < Glossary Index > Finite Number Definition