Irrational Number|Definition & Meaning

Irrational numbers are those that cannot be expressed as fractions. An irrational number cannot be written as just a ratio, such as p/q, where p and q are positive integers and q is greater than zero. 

It is inconsistent with rational numbers. Irrational numbers are typically written as R\Q, where the backslash signifies “set minus.” It is also possible to write the difference between the real numbers and the rational numbers as R – Q. The following figure shows the irrational number.

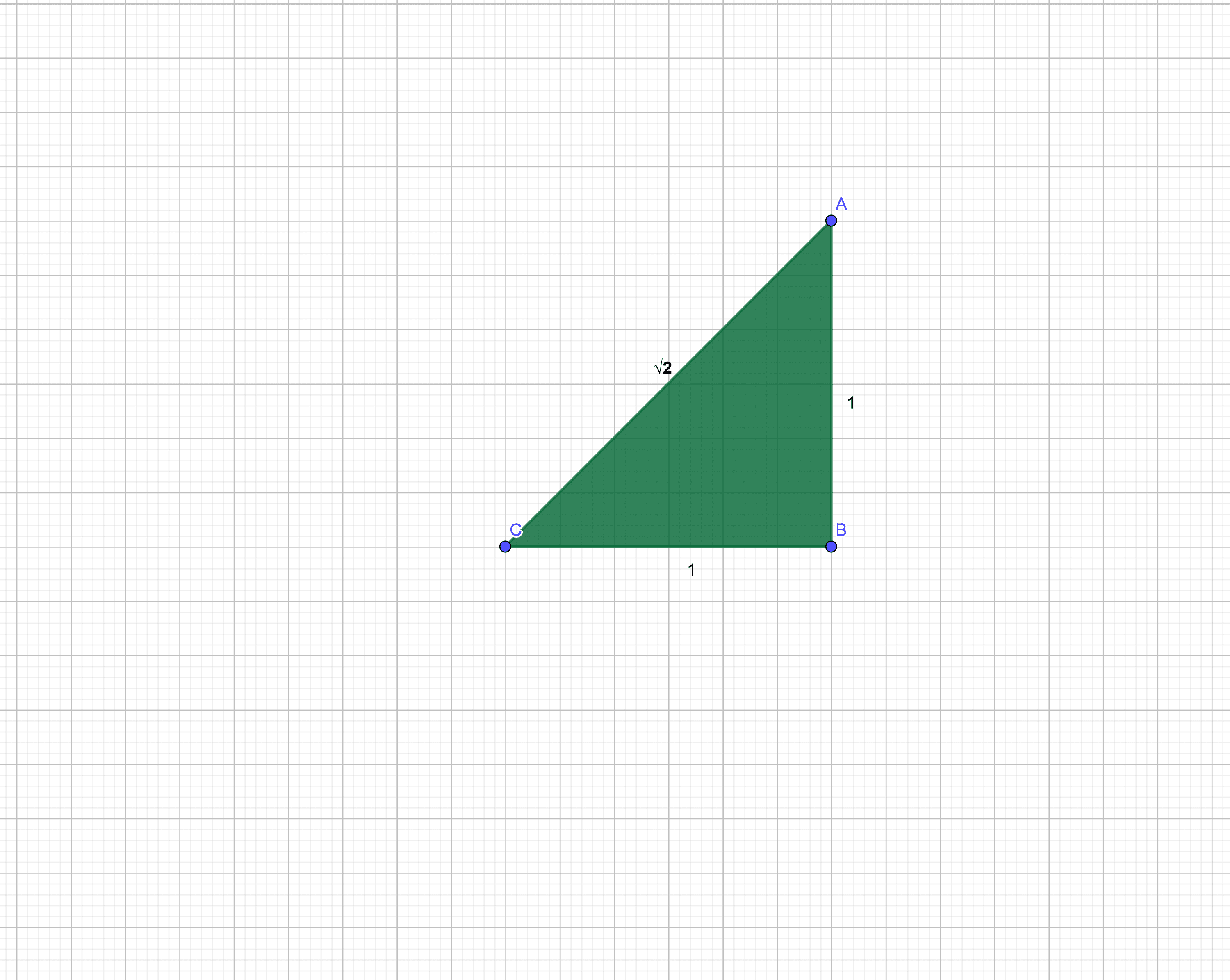
Figure 1 – Hypotenuse showing the irrational number

What Constitutes Irrational Numbers?

Irrational numbers are real numbers that cannot be represented like a ratio of integers. For example, -2 is indeed an irrational number because it can’t be represented as a ratio of two integers. We cannot represent any irrational number as a ratio, such as p/q, where p and q are integers and q is less than zero.

What Sort of Numbers Fall Within this Category?

Good examples of irrational numbers that are frequently used include pi (=314159265…), 2, 3, 5, Euler’s number (e = 2718281…), 2.010010001…., etc.

How Can You Tell Whether a Number Is Irrational?

Irrational numbers are real numbers that cannot be stated in the form of p/q, where both p and q are integers and q is less than zero. These real numbers are known as being irrational. Irrational expressions include things like 2 and 3, amongst others.

In contrast, the term “rational number” refers to any number that can be expressed as the fraction p/q, provided that both p and q are integers and that q is not equal to zero.

Is the Number Pi an Irrational Value?

Pi is considered to be an irrational number because it does not terminate or repeat in decimal form. In addition, 22/7 is indeed a rational number, whereas pi is indeed an irrational number; hence, the two quantities cannot be comparable. The calculated value of pi is 3.141592653589…………..

An illustration of pi, which is irrational, is shown below.

Figure 2 – Illustration of a pi

An illustration of Euler’s number e, which is irrational, is shown below.

Figure 3 – Irrational number

Irrational Numbers’ Inherent Characteristics

As a result of the fact that irrational numbers are subsets of real numbers, irrational numbers are subject to all of the characteristics that are associated with the real number system. Irrational numbers have the following characteristics as a result of their nature:

• Irrational numbers can be created by adding them to rational ones. For illustration, suppose x is irrational, and y is rational, and that the sum of the two, x + y, is also irrational.
• Any irrational number multiplied by a nonzero rational number yields another irrational number. Let us assume that x is irrational, but if xy=z, then x = z/y is rational. As a result, we can conclude that xy is an irrational product.
• There is no guarantee that the (LCM) of any pair of irrational numbers even exists.
• In contrast to the set containing rational numbers, the set containing irrational numbers does not become closed when the process of multiplication is applied to it.

What Applications Do Irrational Numbers Have In Everyday Life?

Irrational numbers are used in various components of life. Obviously, you may not be able to visualize it, but several components use irrational numbers.

1. Trigonometric Ratios need irrational numbers. The ratios are used in various height and distance measurements and also in several calculations in physics.
2. Pi (π) – Circles make no sense without π. Trigonometric Ratios also use π. Several Integrals use it, and it is also used in Polar Coordinates
3. Euler’s Number e – Used extensively in Logarithms and Algebra.

These components may not directly be used, but are used extensively in Engineering. Engineering revolves around designing things for real life, and several things like Signal Processing, Force Calculations, speedometers, etc., use irrational numbers. Calculus and other mathematical domains that use these irrational numbers are used a lot in real life. Irrational Numbers are used indirectly.

Do Irrational Numbers Represent Real Numbers?

Most irrational numbers are regarded as real numbers in mathematics, which is not rational. This implies that irrational numbers can’t be stated as the ratio of two other integers in any way. Non-perfect square roots, for example, will always yield an irrational value.

Sum of an Irrational Number

The addition of two rationales also results in a rational number. A rational number may be stated as a fraction having integer values in both the numerator and the denominator, according to the meaning of the term (denominator not zero).

Since integers are generally closed under addition and multiplication, adding two rational numbers is the same as adding two fractions of the same form, which will result in another fraction of the same form since integers have been closed under addition. The addition of two rational numbers results in the production of a third rational number.

Two irrational integers added together are still irrational, but only sometimes. When adding two irrational integers together, the result is sometimes irrational. The aggregate will be rational, nevertheless, if the irrational components cancel out one another to zero.

Product of an Irrational Number

Multiplying two rational integers yields a rational result. A rational number can be written as a fraction with numerator and denominator values that are both integers (denominator not zero).

Since integers are generally closed under multiplication, multiplying two rationals is equivalent to multiplying two such fractions, leading to yet another fraction of this kind. As a result, a rational number may be obtained by multiplying two rational numbers.

It is not always the case, but irrational numbers multiplying together produce irrational results. An irrational result can occur by multiplying two irrational integers together. But it’s feasible that the product of two irrational integers might be rational.

A Numerical Example of an Irrational Number

Example

Find the irrational numbers between two numbers which are 5 and 6.

Solution

We are required to find the 5 irrational numbers between the given two numbers, which are 5 and 6.

So we need to multiply the given number by 6.

 5 = 5 × (6/6) = 30/6

6=6 × (6/6) = 36/6

Thus, as a result, the five rational numbers that fall between 5 and 6 are as follows:

• 31/6
• 32/6
• 33/6
• 34/6
• 35/6

All mathematical drawings and images were created with GeoGebra.

Inverse Property Of Multiplication Definition < Glossary Index > Irregular Polygon Definition