Normal|Definition & Meaning

A normal is a line, ray, as well as vector which is perpendicular to some other object in geometry. For instance, the infinite line perpendicular towards the tangent line to a curve at a particular location is the normal line to the curve in the plane at that point.

Algebraic signs on a normal vector’s components can denote the number of sides an object has, and its length can describe the object’s curvature.

A vector that is perpendicular to a tangent plane of a surface at a given location in three dimensions constitutes a surface normal, also known as a normal, to that surface at that point. 

A line that is normal to such a plane and many other things are all examples of adjective uses of the word “normal.” The idea of orthogonality can be generalized from the principle of normality.

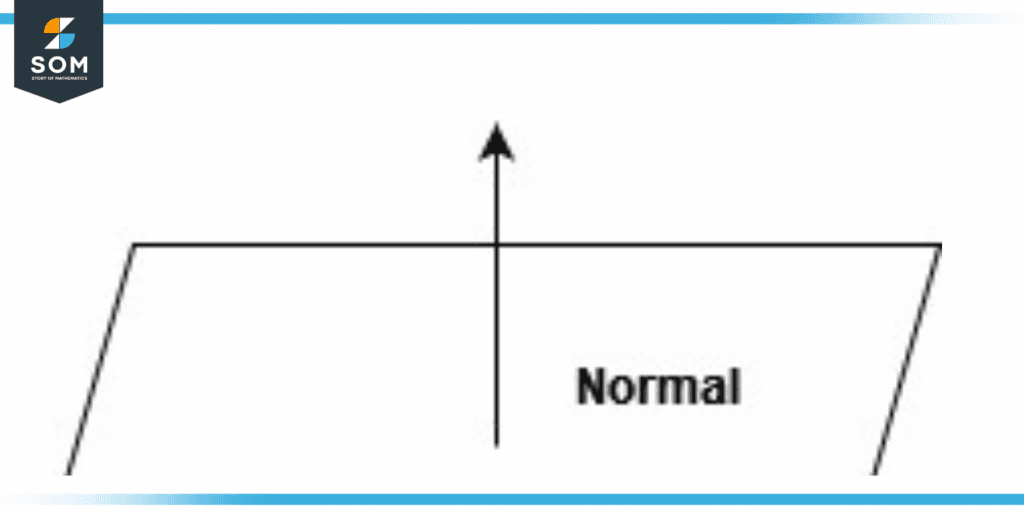
Figure 1 – Parallelogram showing the normal

What Are Normal and Tangent in Mathematics?

Tangent

If we are driving a car around a curve, when we drive over anything slick on the road (such as oil, ice, water, or loose gravel), and our automobile starts to slide, this will continue in such a direction that is tangent towards the curve.

If we grasp a ball in one hand and swing it through a circular motion, then let go of it, the ball would fly off in a direction that is perpendicular to the motion that it was being performed. The spokes of a bicycle wheel are parallel to the rim. A bicycle wheel’s spokes should be aligned perpendicular to the rim.

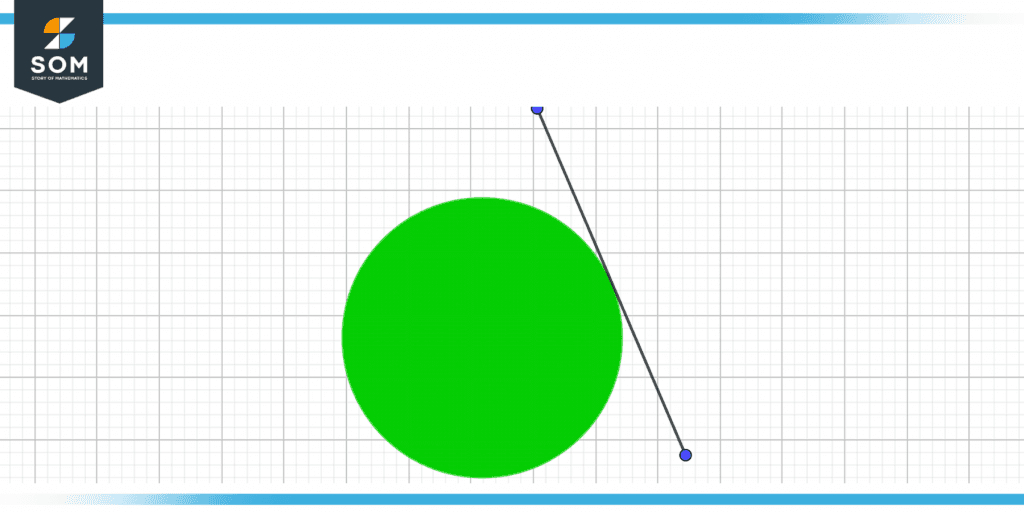
Figure 2 – Circle showing the tangent

Normal

When driving quickly around with a circular path in an automobile, the force which you sense pushing you outwards goes normal to the curvature of the road. This is the case even if the track is not circular.

It is interesting to note that the force that’s also causing you to travel around at that corner is directed specifically toward the center of the circle, and it is acting in a direction that is normal towards the circle. At every point where a spoke joins with the center of the wheel, it is positioned so that it is normal towards the circle form of the wheel.

The lines that are linked with curves like circles, parabolas, ellipses, and hyperbolas are referred to as tangents and normal.

A line is said to be tangent to a curve when it touches the curve at exactly one point, and this particular point is referred to as the contact point. At the point of contact, the normal is a line that runs in a direction that is perpendicular to the tangent.

Tangents can be created to a curve in a variety of different ways, one for each of the individual points that make up the curve. Because both the tangents and the normal are composed of straight lines, their mathematical representation is that of a linear equation between x and y.

The equation for the tangent and the normal can be written in a general form as ax + by + c = 0. Both the equation of a tangent as well as the equation of a curve can be solved using the contact point as a reference point.

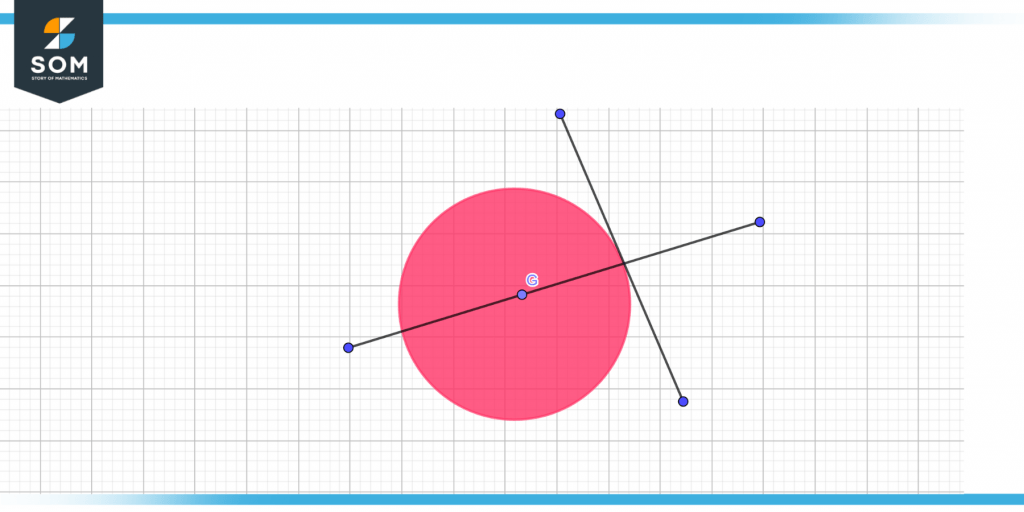
Figure 3 – Circle showing tangent and normal

Normal and tangents are the lines that define curves. Each of the curve’s points has a tangent, which is just a line that touches the curve at that point. The normal is the line that cuts through the contact point perpendicular to the tangent.

Why Do We Need Normal and Tangent?

When we are analyzing the forces that are operating on a moving body, we frequently need to locate the tangents and normal of the curves. A line is said to be tangent toward a curve if it meets the curve at exactly one place and if the slope of the line at that point is the same as the slope of the curve whereas a line that is perpendicular toward a tangent to a curve is referred to as the curve’s normal.

Uses of the Surface Normal

Surface normals are important for defining vector field surface integrals.

They are also frequently utilized in 3D computer graphics for the purpose of lighting computations, and normal mapping is frequently employed to make necessary adjustments.

Tangent and Normal Properties

Understanding tangents and normal are made easier by considering their respective qualities.

• Normal and tangents are parallel to one another.
• A tangent’s and a normal’s combined slopes are equal to -1.
• Normal are inside the curve, while tangents are outside it.
• There is a normal for each tangent of the curve.
• The focus or center of the curve may not always be crossed by the normal curve.
• Normal and tangents are both straight lines that are modeled by linear equations.
• A curve can have an endless number of tangents traced to it.

What Is the Connection Between Tangents and the Normal?

The tangents and the normal are two names for the lines that intersect a circle at this point. While the tangent at that location is parallel to the circle, the normal direction of motion is perpendicular towards the curve. There is a gradient equal to m along both the tangent and the normal if the slope of the curve is m.

Two lines that link curves are tangents and normal. Each point on the curve has a tangent or even a path that crosses the circular at a specific location. Only at the touch point, a normal line is perpendicular to the tangent. A horizontal line that intersects the curve up until a given point is the tangent of such a curve.

Only the precise area that was previously indicated is touched; the curve is not crossed. Such a tangent has a horizontal line perpendicular to it.

A Numerical Example of Calculating a Normal

Example

Determine the equation of the normal to the circle using the following:

\[2x^2 + 2y^2 -2x -5y +3 = 0 \text{ at }(1,1)\]

Solution

We know that:

The circle center is:

\[\left(\frac{1}{2},\frac{5}{4}\right)\]

Then, the equation to the normal circle passing through the given point is:

x + 2y = 3

All mathematical drawings and images were created with GeoGebra.

Nonlinear Equation Definition < Glossary Index > Normal Distribution Definition