Plane Shape|Definition & Meaning

What Is a Plane Shape? 

In mathematics, a plane shape is a 2-dimensional flat shape with no thickness. It is also known as a plane figure or 2-dimensional shape. The term 2-dimensional refers to the fact that these shapes have length and width.

A plane shape may be a combination of sides and corners. Some plane shapes are square, rectangle, circle, triangle, rhombus, etc.

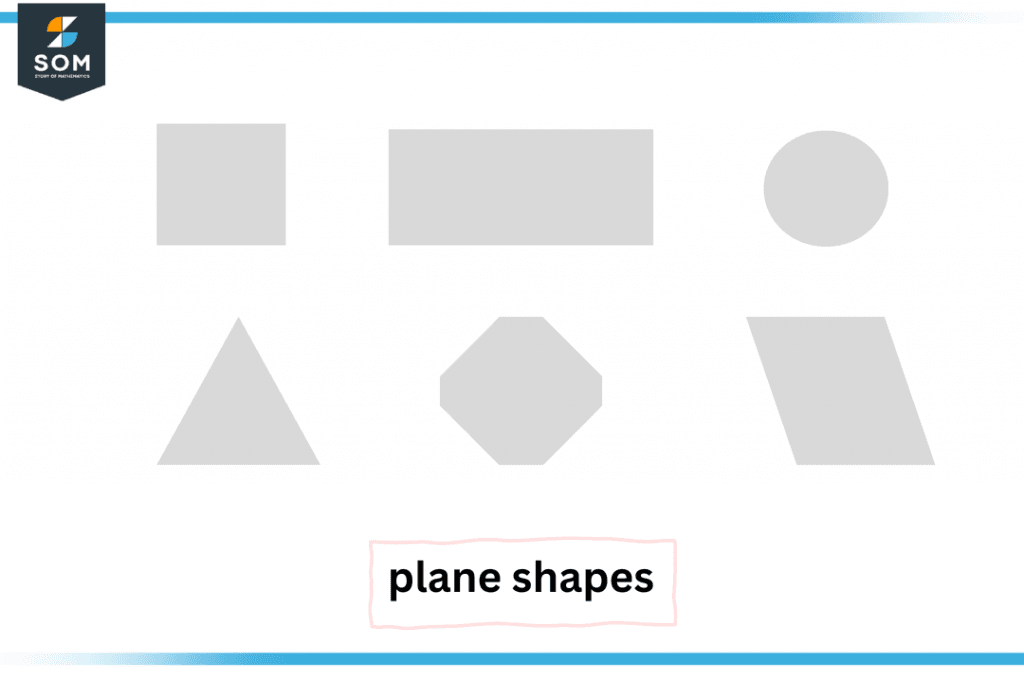
Figure 1 – A few examples of plane shapes

Sides and Corners of Plane Shapes

Plane shapes are a combination of sides and corners. The line segment that makes up a plane shape is called the side. The point where the two sides assemble is called the corner.

Different plane shapes have different numbers of sides and corners; for example, rectangles and squares have 4 sides and 4 corners, whereas a triangle has 3 sides and 3 corners.

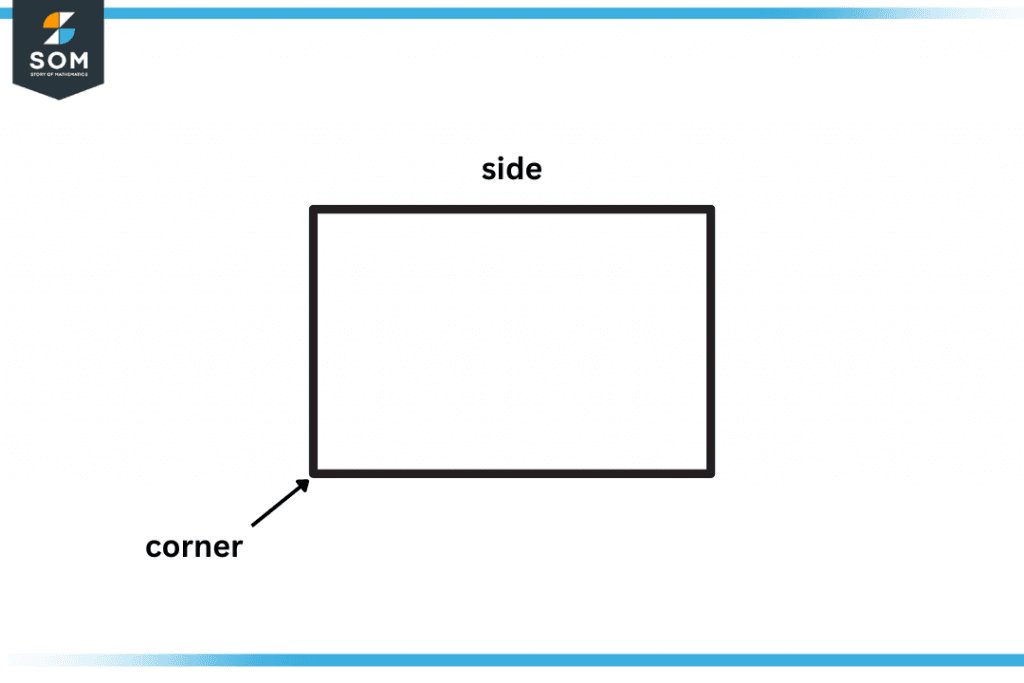
Figure 2 – A visual representation of sides and corners of a plane square

Types of a Plane Shape

There are two types of plane shapes, i.e., open and closed shapes.

Closed Plane Shapes

The 2 dimensional flat, closed surfaces are called closed shapes. They have sides, corners, and faces and are joined by line segments.  In our daily life, we see many examples of closed-plane shapes, such as a cookie, chess boards, currency notes, books, laptops, balls, slices of pizza, bricks, and many more. There are many kinds of plane shapes. Here, we will discuss a few of them.

• Square
• rectangle
• circle
• Triangle
• Pentagons
• Hexagons
• Rhombus
• Trapezoids
• Parallelogram

Square

A square is a flat, 2-dimensional plane shape with 4 sides, 4 corners, and 4 faces. Its construction comprises four line segments joined together. All four sides are equal in length. It has four right angles. Diagonals bisect each other at 90 degrees. If a four-sided shape has equal sides and right angles at corners, that’s a square.

Some daily life squares are a chess board, pizza box, keyboard keys, photo frame, bread, Rubik’s cube, cheese slice, etc.

Rectangle

A rectangle is a flat, 2-dimensional plane shape with 4 sides, 4 corners, and 4 faces, but it differs from a square. How? A rectangle has unequal sides, but opposite sides are equal and parallel to each other. It has four right angles at the corners.

A rectangle has 2 diagonals that bisect each other and are equal in length. Some examples of rectangles are blackboards, television, mobile phone, currency note, books, laptops, doors, a sheet of paper, etc.

Circle

A circle is a plane shape with no corners; rather, it only has a curved boundary. It is a set of points that are at a fixed distance from the center. It has no sides, no corners, and no diagonals. The line segment that divides a circle into two halves is the diameter.

Some examples of circles are football, round wall clock, pizza, wheel, rings, cake, buttons, CDs, full moon, etc.

Triangle

A triangle is a 2-dimensional plane shape with 3 sides, 3 corners, and 3 angles. The angles and sides of a triangle may or may not be equal depending on the type of triangle. The 3 angles of a triangle give a total of 180 degrees.

Acute triangles, obtuse triangles, isosceles triangles, right angle triangles, etc., are some types of triangles. Daily life examples of triangles are slices of pizza, sign boards, sandwiches, etc.

Pentagon

A pentagon is a five-sided 2-dimensional plane shape. It is a type of polygon with 5 corners. It has 5 angles which makes a total of 540 degrees. A pentagon has 5 diagonals. Daily life examples of a pentagon are cupcakes, diamonds,  etc.

Hexagon

A hexagon is a flat 2-dimensional plane shape with 6 sides, 6 corners, and 6 angles. A regular hexagon has all the sides equal in length. All the interior angles of a regular hexagon measures 120 degrees, and all the exterior angles measure 60 degrees.

It has 6 lines of symmetry and 6 angles of rotation. Real-life hexagons are honeycombs, nuts, tie knots, white divisions of a volleyball, etc.

Rhombus

A rhombus is a plane shape having all 4 sides equal and opposite sides parallel. In a rhombus, the angles opposite to each other are equal in length. Diagonals of a rhombus bisect each other perpendicularly.

Trapezium

A trapezium is a 2-dimensional plane shape with 4 sides and one pair of parallel sides. The parallel sides are known as bases, and the non-parallel sides are legs. Right trapezium, isosceles trapezium, and scalene trapezium are the 3 types of trapeziums. If we add all the angles of a trapezium, it gives us a total of 360 degrees.

Parallelogram

A Parallelogram is a plane shape with opposite sides equal and parallel. Diagonals of a parallelogram are unequal in length and bisect each other at the midpoint. A parallelogram has opposite equal angles.

Area and Perimeter of Closed Shapes

The area of the plane shape is the entire region surrounded by the boundary of the figure in a 2-dimensional plane. Perimeter is the path covered by the boundary in a 2-dimensional plane.

The area and perimeter of some plane shapes are as follows:

Square

Area of square = a$^2$

Perimeter of square = 4a

Rectangle 

Area of rectangle = a x b

Perimeter of rectangle = 2(a+b)

Circle

Area of circle= pie.r$^2$

Perimeter/circumference of circle = 2pie.r

Triangle 

Area of triangle= 1\2(base x height)

The perimeter of the triangle= sum of all sides

Pentagon

Area of pentagon= 1\2(perimeter x apothem)

The perimeter of a pentagon= 5 x sides

Hexagon

Area of hexagon = 1\2(perimeter x apothem)

The perimeter of the hexagon =6 x sides

Rhombus

Area of rhombus = 1\2(product of diagonals)

The perimeter of the rhombus = 4 x side

Trapezium

Area of trapezium = 1\2 x (a+b) x h

The perimeter of the trapezium = sum of all sides

Parallelogram

Area of parallelogram = base x height

Perimeter of parallelogram = 2(base+height)

Polygonal and Non-polygonal Plane Shapes

Closed shapes can further be characterized into polygonal and non-polygonal plane shapes. A polygon is formed only by line segments and has at least 3 sides. If any side of a plane figure is not straight (curved), it is not a polygon.

Squares, rectangles, parallelograms, trapeziums, etc., are examples of polygonal plane shapes, whereas circles, ovals, ellipses, etc., are examples of non-polygonal plane shapes.

Open Plane Shapes

Open shapes are a combination of line segments and corners, but they have at least one opening, i.e., any one of the corners is not connected to the side. It may be a straight or curved line or any other irregular shape that has an open face. Angles are an example of open shapes.

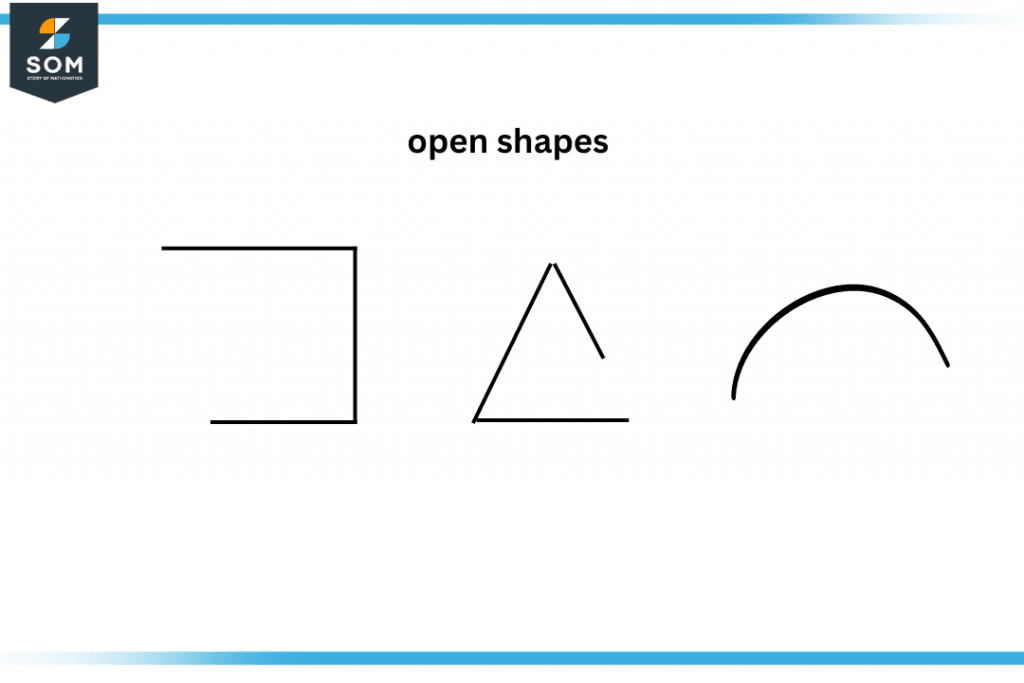
Figure 3 – Open plane shapes

Solid Shapes

In mathematics, a solid shape is a flat, closed and 3-dimensional figure. The term 3 dimensional refers to the fact that these figures have length, width, and height. Cuboids, spheres, cylinders, and cubes are some examples of solid shapes.

As plane shapes refer to 2-dimensional figures, solid shapes are 3-dimensional figures. Plane shapes are easy to construct, whereas solid shapes are quite complex to construct.

Solved Examples Related to Plane Shapes

Example 1

Calculate the area and perimeter of a parallelogram whose base and height are 10m and 5m, respectively.

Solution

Given:

base=10m

height=5m

Area =?

perimeter=?

The formula for the area and perimeter of the parallelogram is:

Area = base*height

A = 10m*5m

A = 50m$^2$

Perimeter = 2(base*height)

P = 2(10m*5m)

P = 2(50)

P = 100m

Hence, the perimeter of the parallelogram is 100m, and the area is 50m$^2$.

Example 2

What is the circumference of a circle with a radius of 5cm?

Solution

Given radius = 5cm

Circumference =?

To find the circumference, we use the formula

Circumference = 2*pie*r

C = 2*pie*5cm

C = 31.4cm

Hence, the circumference of the circle is 31.4cm.

All images are created using GeoGebra.

Plan Definition < Glossary Index > Plot Definition