Point Symmetry|Definition & Meaning

In geometry, many factors are associated with symmetry. The concept of symmetry is utilized by professionals, artists, jewelry and clothes designers, architects, and many others for different jobs according to their professions and needs. There can be found symmetrical motifs in every place: flowers, beehives, handkerchiefs, religious symbols, and rugs. 

When Does Point Symmetry Occur?

In this figure, the origin or central point is labeled O. The shape consists of two diagonals showing the distances of all vertices from the origin are the same.

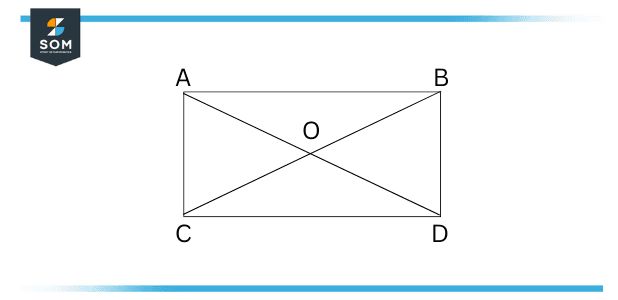
Figure 1 – Rectangle Point Symmetry

Point symmetry takes place in many kinds of objects and shapes. For point symmetry to happen, there must be a dividing part or central point that breaks the shape or object into two equal parts which are labeled here as Part A and Part B. Every point in Part A should have a matching point in Part B whose distance from the central point is just as same as the opposite point and lastly, the directions of Part A and Part B must be opposite.

You can physically observe point symmetry by looking in a mirror, and when you touch the mirror with your finger, where your finger touches the mirror is the point. It looks like you are inseparably hooked to your image.

An important rule in point symmetry is that there should be a point where they connect (the point where your finger is touching the mirror). An object is said to have point symmetry when you turn an object upside-down and it still looks the same. The figure and the matching part must face the same way.

How to Test for Point Symmetry

To check if an object has point symmetry, match the object with the opposite side after rotating it on its central point or origin. if both objects match then, it has a point symmetry.

Point symmetry happens when we are given a central point on a shape and every point is at the same distance on both sides from the central point. Different words that can be utilized rather than point symmetry are origin symmetry (another word for the central point is the origin) and rotational symmetry. When looked at from opposite directions, the object will look exactly the same.

Visual Examples of Point Symmetry

Point symmetry happens when there is a place or a point on an object from where the object can be divided into equal and identical parts. The central point divides the object or shape into two parts. Each part has a connected part on the other side whose distance from the central point is the same as the other. Both parts are placed in opposite directions.

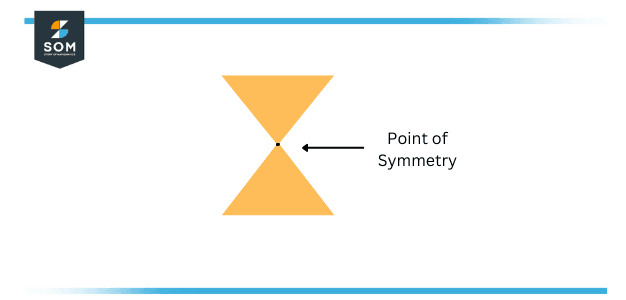
Figure 2 – Illustration of Point Symmetry

When an object is made around a single point, it has point symmetry and that single point will also be the point of symmetry. This spot is known as the object’s center or the symmetry’s center. In the figure underneath, you can see a point marked X′ on the opposite side of the center that reflects point X on the figure and is directly inverse to X and is on the figure. The figure is symmetrical around the center as proved above.

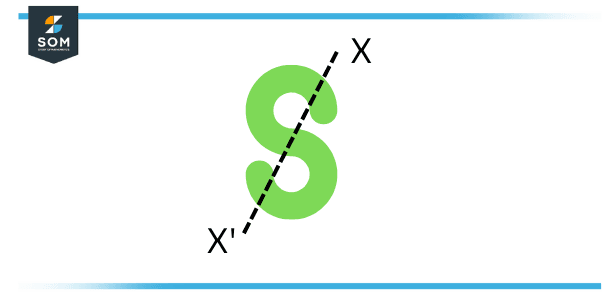
Figure 3 – Symmetric Around the Center Example

When after rotating a figure 180∘, it comes back to its original form, we can say that it has point symmetry.

Point Symmetry vs. Reflection

Line symmetry, or reflection, is an object having a line of symmetry and not just a point that, when folded on this line, one side would match the other side completely. When a person is having a look at their reflection on standing water. This is not the same as point symmetry. An object or shape can have point symmetry but not line symmetry. It is also possible for an object or shape to have both line symmetry and point symmetry at the same time. An object or shape might also have multiple lines of symmetry.

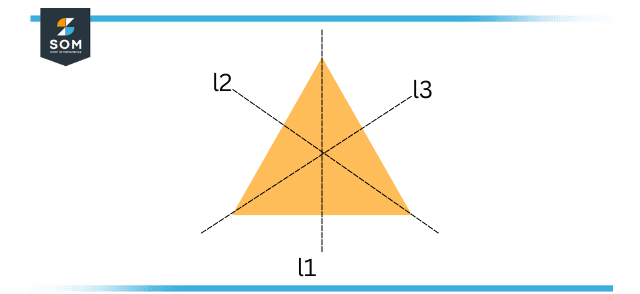
Figure 4 – Triangle Line Symmetry

The triangle shown above has multiple lines of symmetry because a line of symmetry can be drawn from one vertex to the center point of the other side. This line of symmetry will split the shape completely in half. When folded from the line of symmetry, one side of the object would fit completely in comparison to the other side. The triangle has three total lines of symmetry. It does not have point symmetry.

Point Symmetry in Letters

The symmetry point is a point that acts as a sort of center point for the object. If a line is drawn via the point of symmetry and it travels across the figure on one side of the point, then the line will also cross the diagram at a similar distance from the point on the other side of the point as well.

If all the parts of an object have a matching part, it will also have point symmetry. Point symmetry can also be seen in the English alphabet. The related sections of central point O are in opposing directions.

Point symmetry can be found in the following capital letters: H, I, N, O, X, and O. Point and line symmetry can be tracked down in the letters H, I, O, and X.

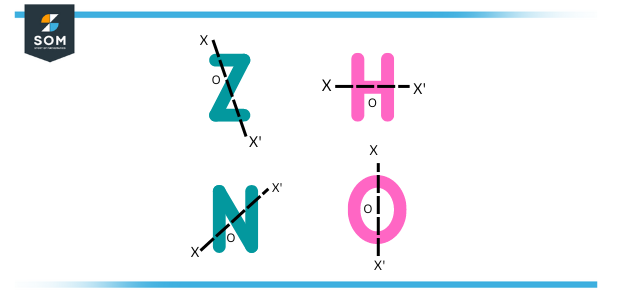
Figure 4 – Triangle Line Symmetry

Solved Examples: Point Symmetry

Which of the following letters of the English alphabet has a point symmetry yet doesn’t have a line of symmetry?

1. H
2. I
3. Z
4. X

Solution

A line that cuts a figure into two matching parts is a line of symmetry.

For the letter Z, the point symmetry applies and is true, but for line symmetry, it does not apply. In comparison, both point and line symmetry can be applied to the letters H, I, O, and X.

Therefore, the correct answer is option Z.

All images/mathematical drawings were created with GeoGebra.

Point Definition < Glossary Index > Population Definition