Power Set|Definition & Meaning

The cluster of all subsets of a full set S is a collection of sets. Therefore, the power set of a provided set is always full. This set is stated to be the power set of S and is indicated by P(S). If S possesses N components, then P(S) has $2^n$ subsets.

Figure 1 – Power Set Depiction

What Is a Power Set? 

A power set is expressed as the set or set of each and every subset for a piece of provided set, as well as the vacant set, which is represented by {}, or $\phi$. A set that contains ‘n’ elements has 2n possible subsets in full.

For instance, let Set A = {1,2,3}. Hence, the whole numeral of elements in the set is 3. Consequently, the power set contains $2^3$ elements. Let us find the power set of A.

A = {1, 2, 3}

Subsets of Set A = {}, {3}, {2}, {1}, {1, 2}, {1, 3}, {2, 3}, {1, 2, 3}

Power set P(A) = { {}, {3}, {2}, {1}, {1, 2}, {1, 3}, {2, 3}, {1, 2, 3} }

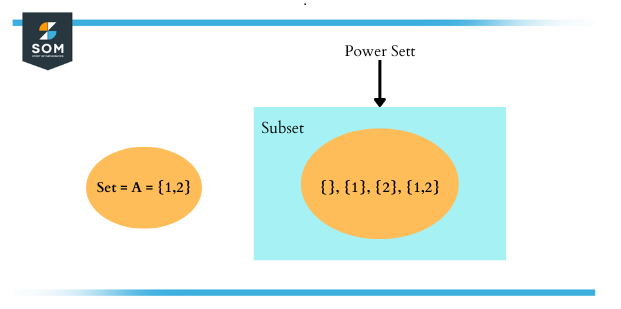
Figure 2 – Power Set Venn Diagram

Visual Example of a Power Set

Let’s glance at a pictorial to witness just how multiple subsets you can obtain out of a set. I am intending to use ice cream for this sample: strawberry, chocolate, and vanilla. Noted algebraically utilizing abbreviations, the set would seem like this: {S, C, V}. So, how numerous subsets can we gain out of this three-element set?

The query can actually be presented as “In how many distinguishable methods can these three articles be organized”?

Foremost, you own a subset of zero, or { }. Remember that a null set is a subset of every set.

At the moment, you keep a subset comprising each flavor by itself: {S}, {C}, and {V}. The following set of subsets would be the distinct union of two options each, such as {S, C}, {S, V}, and {C, V}. The last subset is the subset that comprises all the elements: {S, C, V}. These eight alternatives are each and every probable subset for the set {S, C, V}.

Concurrently, each and every one of these subsets makes a power set. A power set is one that includes all of the probable subsets of a given set. The power set is mentioned like this: P(S) =. So, for our ice cream illustration, the power set memo would be:

P(S,C,V) = {{ }, {S}, {C}, {V}, {S, C}, {S, V}, {C, V}, {S, C, V}}

Did you see that the sets of all of the elements and none of the elements are subsets, as well as every mixture of the elements? That is necessary to recall.

Numerical Example of a Power Set

Why would you ever require to utilize power sets in algebra (or in actual life, for that matter)?

Also, power sets can be utilized to specify all the various ways things can be placed concurrently. Perhaps you ought to sort out the various probable groups for a set of learners, or possibly you want to calculate how to identify a group of objects in a store window; you can utilize power sets to determine all the diverse ways you could group your objects concurrently.

While another usage for them is deciding each and every factor of a number. Power sets are an outstanding means to discover every single element for any digit possible.

Okay, so can you describe to me all of the elements/factors behind the number 130? (Remember that a factor is a number that can be multiplied by another digit to result in the presented product.)

To decide all of the factors for 130, we first begin by pinpointing the prime factors, which are those factors that are only divisible by themselves, and 1.

The set of prime factors for 130 is (S) = {2, 5, 13}

Now, we develop a table to explain the power set of this set of prime factors.

The foremost row in the table is the blank set (empty set), and a factor of 1 is allocated because 1 is the multiplicative identity.

The following three rows are the subsets having a single element; the real element will be the resultant factor. The successive three rows are subsets with only 2 elements. The factor enumerated is the by-product of the two elements in the subset.

Ultimately, you have the subset, which comprises all the elements from the actual set, and the factor is, certainly, the allocated number from the sample.

The Cardinality of the Power Set

Cardinality depicts the full number of elements existing in a set. In the matter of a power set, the cardinality will be the list of the number of subsets of a set. The numeral of elements of a power set is noted as |P (A)|, where A is any set. If A has ‘n’ elements, then the procedure to discover the number of subsets of a set in a power set is presented by:

|P(A)| = 2n

For instance, set A = {a, b, c}

n = number of elements of A = 3

So, the numeral of subsets in a power set of A will be:

Subsets of A = {}, {a}, {b}, {c}, {a,b}, {b,c}, {a,c}, {a,b,c}

P|A| = 23 = 8

Therefore, P(A) is {{}, {a}, {b}, {c}, {a,b}, {b,c}, {a,c}, {a,b,c}}

Power Set Properties

A power set is one that holds a checklist of all the subsets of a provided set. The power set, which is indicated by P(A) with ‘n’ elements, has the given qualities:

• The whole number of elements of a set is 2ⁿ.
• A null set is an actual element of a power set.
• The power set of a null set has only one element, and that is the null set itself.
• For a set with a limited number of elements, the power set is finite. For instance, the power sets are enumerable if set X = {b,c,d}.
• The power set of an unlimited set carries an infinite number of subsets. For illustration, if Set X holds each and every multiple of 10 starting from 10, then we can state that Set X has an endless number of elements. Although there is an indefinite number of elements, a power set yet exists for set X. In this situation, it has a limitless number of subsets.
• The power set subsists for both finite and infinite sets.

Solving an Example Problem of a Power Set

Q.1: Discover the power of the below set and also encounter the entire number of elements.

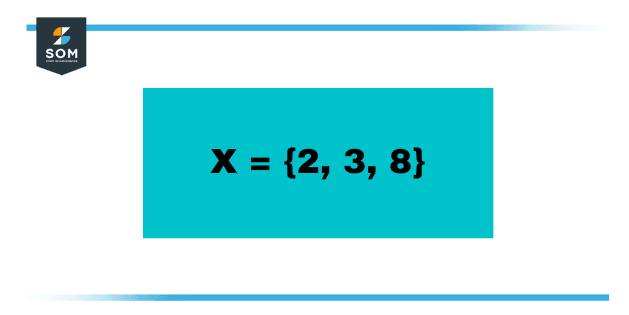
Figure 3 – Example Problem

Solution

Given that X = {2, 3, 8}

The whole numeral of elements in the power set is 2$^n$

The entire number of elements in this situation is n = 3.

So, 2$^3$ = 8, which marks eight elements of the power set of X exist.

Consequently:

P(X) = {{}, {2}, {3}, {8}, {2, 3}, {3, 8}, {2, 8}, {2, 3, 8}}

All images/mathematical drawings were created with GeoGebra.

Power Definition < Glossary Index > Precision Definition