JUMP TO TOPIC
Prime Factor|Definition & Meaning
Definition
A prime factor is any factor of a number that is also a prime number. For example, the prime factors of 300 are 2, 3, and 5, as 2 x 2 x 3 x 5 x 5 = 300. We can find all prime factors of a number using prime factorization. The prime factorization of every composite number is unique, which makes them essential in cryptography (Fundamental Theorem of Arithmetic)
What Is Prime Factorization?
The method of factoring a number in terms of prime numbers, which means that all of the factors will be prime numbers, is known as prime factorization. Students will better understand how to quickly determine the prime factors of a number by reading this article, which explains all of the principles of prime factors and the methods for prime factorization.
Prime factors of a number can be determined by the most accessible approach is to divide the real number by prime factors, so the result is equal to 1. By illustration, when we prime factorize the number 30, we obtain the following: 30/2 = 15, 15/3 = 5, 5/5 = 1.
Given that we were given the remainder, it is impossible to factor it further. Therefore, 30 is equal to 2 times 3 times 5, where the factors 2, 3, and 5 are all prime.
When multiplied by any of the natural numbers, these prime numbers give rise to the composite numbers known as composite numbers.
In this article, let’s talk about the definition of prime factorization, the many ways to determine the prime factors of a number, and some examples of problems that have already been solved.
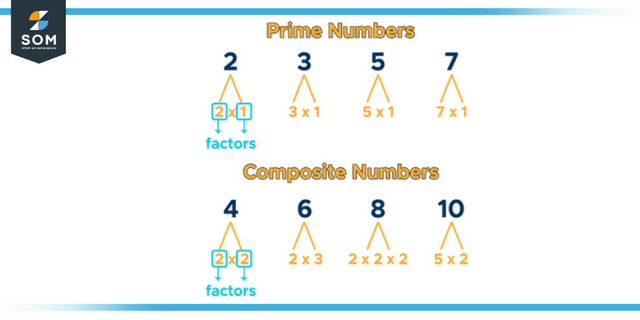
Figure 1: Representation of prime numbers.
Highest Common Factor and the Lowest Common Multiple
The prime numbers produce the composite numbers when multiplied by any natural number or whole number (other than 0), but not by themselves. A prime factorization process is applied to the numbers in question to factorize composite numbers and discover their prime factors. This method is also used to discover the HCF (Highest Common Factor) and LCM (Least Common Multiple) of any given set of numbers.
If you give me any two numbers, then the most significant common factor will be the factor that is both larger and present in both of those numbers, and the least common multiple will be the factor that is both smaller and present in both of those numbers.
A number’s prime factors can be written as:
The prime factors of the integers are the set of prime numbers that, when multiplied by each other, result in the number in question. Additionally, the number can be divided by prime factors. It’s like when you factor a number and only look at the prime numbers among the factors.
As an illustration, the prime factors of the number 6 are the numbers 2 and 3, while the prime factors of the number 26 are the numbers 13 and 2, and so on.
Techniques for Prime Factorization
The following are the prime factorization algorithms that are used most frequently:
- The Method of Division
- The Method of the Factor Tree
- The Method of Division
Finding the factors of a large number involves a series of processes analogous to those used in calculating the prime factors of a smaller number. To get a number’s prime factors using the method of division, proceed through each of the following procedures in order:
Step 1: divide the number supplied by the number that is the smallest prime. The number should be strictly divided in this particular scenario by the smallest prime number.
Step 2: Divide the quotient by the integer with the fewest prime digits.
Step 3: Continue to repeat Steps 2 and 1 until the quotient equals 1.
Step 4: Multiply all of the prime factors together as the final step.

Figure 2: Representation of method of division.
Exemplification of the Division Method for Finding Prime Factors
The technique of factorizing a number into its prime factors is described in depth and step-by-step below, using 460 as an example.
First, divide 460 by the prime number with the fewest digits, 2.
So, 460 ÷ 2 = 230
Step 2: Again, Find the least prime number that may be obtained by dividing 230. (which is again 2).
Now, 160 ÷ 2 = 115
Step 3: Divide once more with the number with the minor prime factor, which will be 5.
So, 115 ÷ 5 = 23
Step 4: Because 23 is a prime number, we may obtain 1 by dividing it by itself.
460 can be broken down into its prime factors as follows: 22 times, 5 times, 23
Method of the Factor Tree
The following steps are used to factor tree approach to obtain the prime factorization of the given number:
Consider the specified number to be the beginning of the tree in the first step.
Step 2: Record each factor in its respective pair as a branch on a tree.
Step 3: Factorize the composite factors once more, writing down the factor pairs as the tree branches.
Procedure 4: Repeat the previous step until all the composite components have been reduced to their prime factors.
In the factor tree algorithm, a number’s factors are first determined, and then those factors’ numbers are factorized repeatedly until we achieve closure.
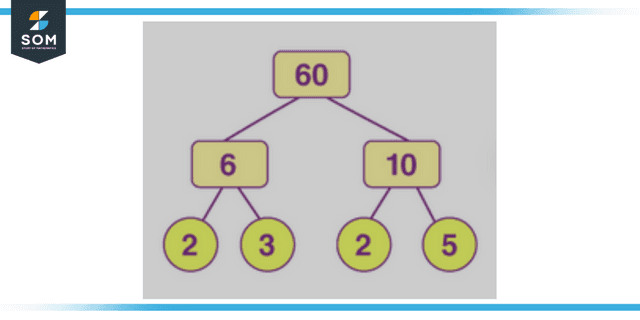
Figure 3: Representation of factor tree.
A Few Examples of Prime Factorization
Example 1
Elsa can run around the track in 4 minutes. Dustin can run the same track in 6 minutes. Ginny can run the same track in 8 minutes, and Mike can run the same track in 5 minutes. If they start at the same time, when will they next meet at the starting line?
Solution
We will find the least common factor of 4, 6, 8, and 5, which is 120.
They will next meet at the starting line in 120 minutes or 2 hours.
Example 2
Write the prime factorization of 50.
Solution
Write 50 as the product of two positive numbers, that are 25 * 2.
Continue factoring until all factors are prime, that are 5 * 5 * 2.
The prime factorization of 50 are 52 * 2
All images/graphs are created using GeoGebra.
