Primitive Function|Definition & Meaning

Figure 1 – Area using integral

Figure. 1 illustrates the area under the curve, which can be found using integral. The two crucial operations in calculus are differentiation and integration. We are aware that integration is the process of discovering a function’s derivative, whereas differentiation is the opposite. 

Assume that a function f is differentiable in the interval V, meaning that each point in V has a copy of the derivative, f’. In such a situation, a straightforward query emerges: Is it possible to identify the function for acquired f’ at each point?

Antiderivatives (or primitive functions) are the functions that may have served as a derivative. The indefinite integral of the function is the name of the formula that generates all of these primitives. And the search for primitives is known as integration. There are two classes of integrals: definite and indefinite integrals.

The function’s anti-derivatives or integrals are not all the same. If C is arbitrarily selected from the set of real numbers, one can generate an endless number of anti-derivatives of each of the various functions.

C is often referred to as an arbitrary constant because of this. The parameter C is used to obtain various anti-derivatives (or integrals) of the supplied function.

Difference Between Definite Integral and Indefinite Integral (Primitive)

An indefinite integral has no integration bounds. When the lower and upper bounds are constants, a definite integral denotes a number. An extended family of functions, whose derivatives are f, is represented by the indefinite integral. Any two-family functions will always differ from one another.

 Properties of Primitive Function

• Differentiation and integration are the exact opposites of one another in terms of process.
• The same derivative on two indefinite integrals results in the same family of curves, making them equal.
• The sum of integrals is the integral of the product of two functions.
• Following are real numbers $p_1$, $p_2$, and $p_n$ for a finite number of functions $f_1$, $f_2$, and $f_n$.

$\int p_{1} f_{1}(x)dx + \int p_{2} f_{2}(x)dx + \ldots + \int p_{n} f_{n}(x)dx$ which will be equal to

$ p_{1} \int f_{1}(x)dx + p_{2} \int f_{2}(x)dx + \ldots + p_{n} \int f_{n}(x)dx$

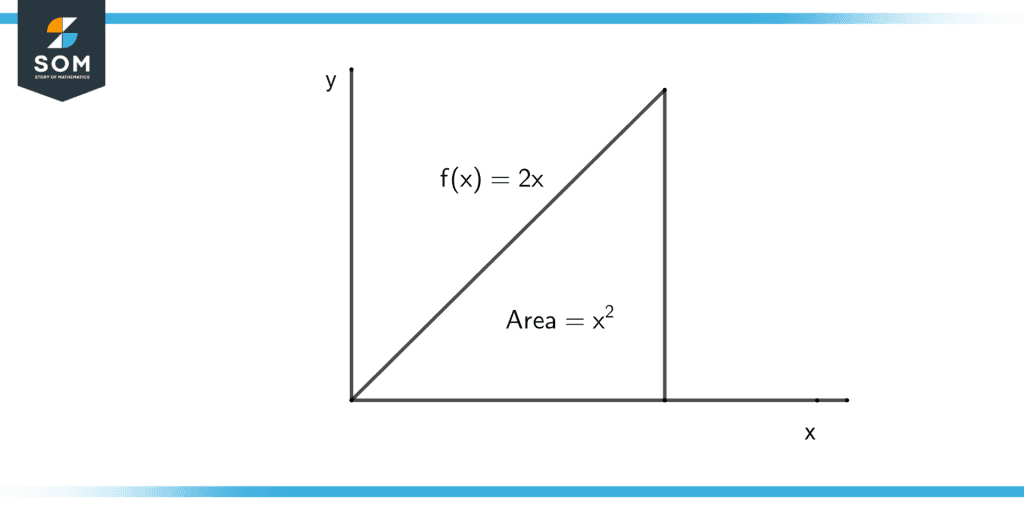
Figure 2 – Area of a triangle

Figure 2 proves that the area under the curve can be found using integrals.

Area of triangle = $\dfrac{1}{2} \times base \times height$

Area of triangle =  $\dfrac{1}{2} \times x \times 2x$

Area of triangle = $x^2$

Some of the Integral Formulae

$\int cos(x) dx$ = sin(x) + c

$\int sin(x) dx $ = – cos(x) + c

$\int sec^{2}(x) dx $ = tan(x) + c

$\int cosec^{2}(x) dx $ = – cot(x) + c

$\int (x)^n dx$ =  $\dfrac{x^{n+1}}{n+1}$ + c

$\int 1 dx$ = x + c

Where c is the constant of integration.

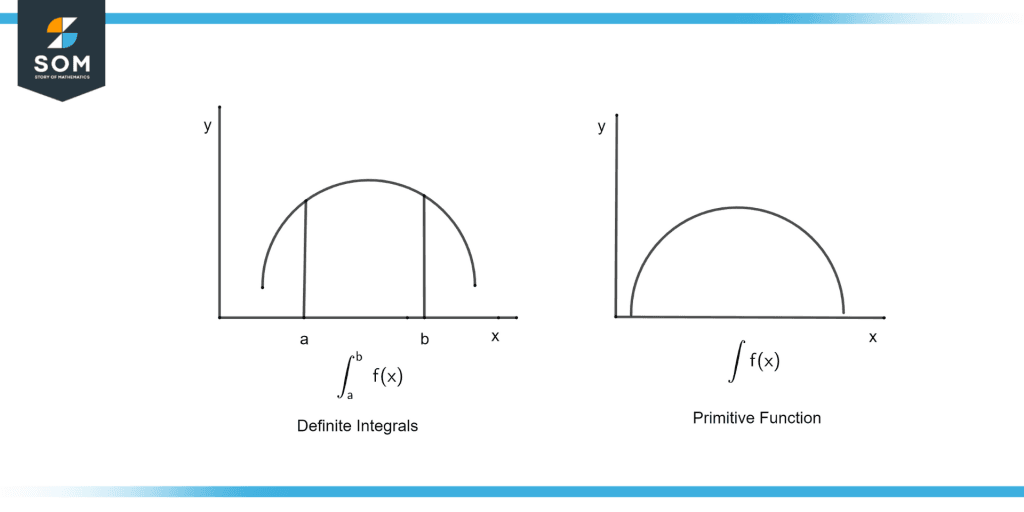
Figure 3 – Difference between definite and indefinite integrals

Figure 3 illustrates the difference between definite integrals and primitive functions. As you can see, the definite integral is bounded by an upper and lower limit, whereas the primitive function is unbounded (i.e., applies over the complete definition of the function from -$\infty to +$\infty$).

Therefore, if you see an integral symbol with limits (-$\infty$, +$\infty$) as in $\int_{-\infty}^{+\infty}f(x)dx$, it represents the primitive function (or indefinite integral) of f(x).

Applications of Integrals

Following are the application of integrals in mathematics:

• To determine the centroid (center of mass) of a region with curved sides.
• To calculate the space between two curves
• Discover the space beneath a curve
• The curve’s average value

Following are the application of integrals in physics:

• The point of gravity
• Vehicle mass and inertia momentum
• The weight and speed of satellites
• Tower mass and momentum
• The mass’s center
• The speed at which a spacecraft was launched into orbit
• The path taken by a spacecraft when it was sent into orbit
• To determine thrust

Difference Between Derivation and Integration

Differentiation is the process of calculating how quickly one quantity changes in relation to another, whereas integration is the process of combining many smaller components into a larger one that functions as a single component.

 In order to determine a function’s slope at a certain point, differentiation is utilized. while integration is used to determine the region beneath the integrated function’s curve.

A function’s differentiation is unique, but its integration might not be since the integration constant C’s value is arbitrary. While definite integrals of functions are thought of across an interval, derivatives are thought of at a single point.

Some Examples of Integrals

Examples 1

Evaluate the given indefinite integral $\int(5x^2 + 3x +1)dx$

Solution

In order to evaluate this indefinite integral, we have to use the power rule, and as we know, the $\int x$ is equal to one, so:

F(x) = $\int(5x^2 + 3x + 1)dx$

F(x) = $\dfrac{5x^{2+1}}{2+1} + 3$

F(x) = $\dfrac{5x^{3}}{3} + 3 + c$

Examples 2

Evaluate the given indefinite integral $\int(5x^3 + 3x^2 +2x + 3)dx$

Solution

In order to evaluate this indefinite integral, we have to use the power rule, and as we know, the $\int x$ is equal to one, so:

F(x) = $\int(5x^3 + 3x^2 + 2x + 3)dx$

F(x) = $\dfrac{5x^{3+1}}{3+1} + \dfrac {3x^{2+1}}{2+1} +2$

F(x) = $\dfrac{5x^{4}}{4} + \dfrac{3x^{3}}{3} + 2 + c$

F(x) = $\dfrac{5x^{4}}{4} + x^{3} + 2 + c$

Examples 3

Evaluate the given indefinite integral $\int(15x^4 + 13x^2 + 2x + 3)dx$

Solution

In order to evaluate this indefinite integral, we have to use the power rule, and as we know, the $\int x$ is equal to one, so:

F(x) = $\int(15x^4 + 13x^2 +2x + 3)dx$

F(x) = $\dfrac{15x^{4+1}}{4+1} + \dfrac {13x^{2+1}}{2+1} +2$

F(x) = $\dfrac{15x^{5}}{5} + \dfrac{13x^{3}}{3} + 2 + c$

F(x) = $3x^{5} + \dfrac{13x^{3}}{3} + 2 + c$

 All images were created using GeoGebra.

Prime Factor Definition < Glossary Index > Prism Definition