Prism|Definition & Meaning

Conceptual Overview

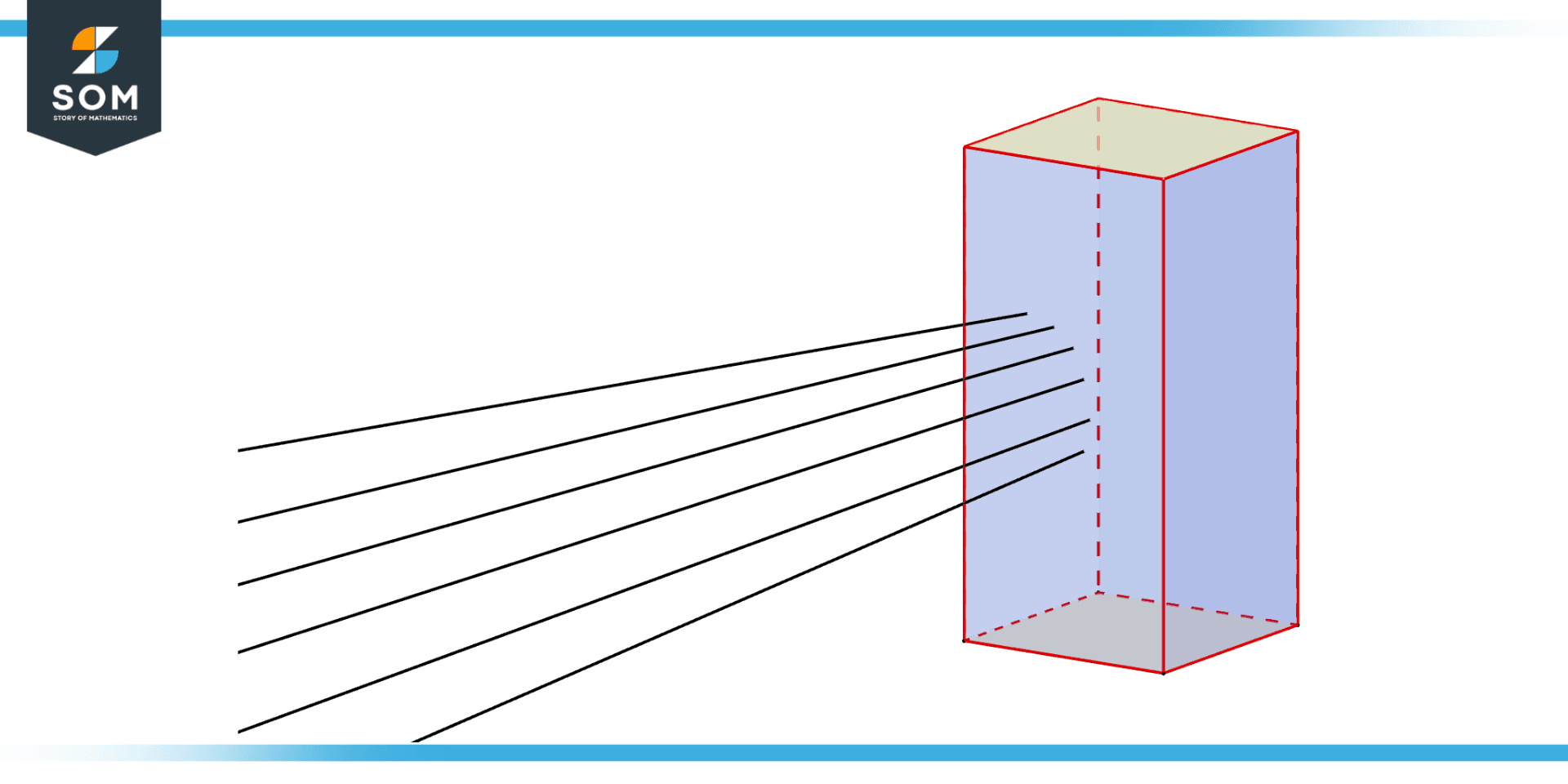
Figure 1 – Ray of light coming from square prism

Prism is a term that is often used in optics and geometry and has a variety of applications in science, technology, and everyday life. In optics, prisms are used to refract or bend light in a specific direction. This property is based on the refractive index of the material from which the prism is made. 

The refractive index is a measure of how much a given material will bend light as it passes through it. When light enters a prism, it is refracted, or bent, as it passes through the material. This refraction occurs because the light waves are slowed down as they pass through the denser material of the prism.

Formula for Prism

There is no specific formula for a prism in general, as the formula for a prism depends on the specific type of prism and the information that is known about it. However, there are several formulas that can be used to calculate various properties of a prism, such as its volume, surface area, and lateral area.

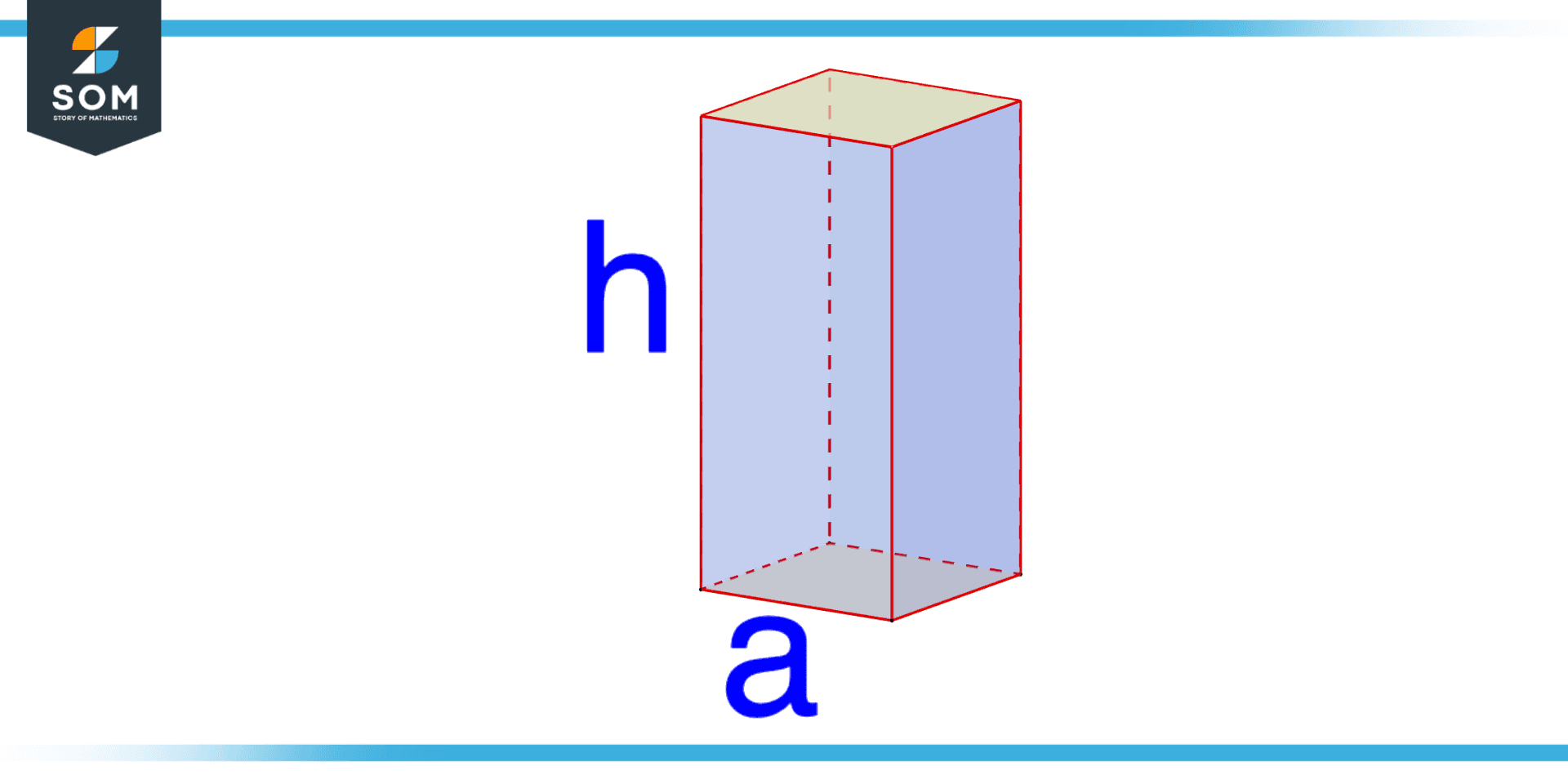
Figure 2 – Volume of Prism

For the volume of a prism, you can use the formula:

Volume = Base Area x Height

Where “base area” is the area of one of the flat, parallelogram-shaped sides of the prism (also known as the base of the prism), and “height” is the distance between the two bases of the prism. The base area can be calculated using the formula for the area of the specific shape of the base (such as a rectangle for a rectangular prism or a triangle for a triangular prism).

Properties of Prism

There are several properties of prisms that are important to understand:

1. A prism is a three-dimensional shape with flat, parallelogram-shaped sides and triangular ends.
2. The sides of a prism are called its bases, and the distance between the bases is called the height of the prism.
3. The triangular ends of a prism are called its lateral faces.
4. Prisms are made of a transparent material, such as glass or plastic, which allows light to pass through them.
5. Prisms have a refractive index, which is a measure of how much they bend light as it passes through them.
6. Prisms can be used to refract, or bend, light in a specific direction.
7. Prisms can disperse light into its individual colors, a phenomenon known as dispersion.
8. Prisms are used in the construction of lenses, windows, lasers, and other optical devices.
9. Prisms are also used in geometry, computer graphics, and 3D modeling.
10. There are several types of prisms, including triangular prisms, rectangular prisms, and pentagonal prisms.

Types of Prism

There are several types of prisms that differ based on their shape and the way they refract light. Some common types of prisms include:

Triangular Prism

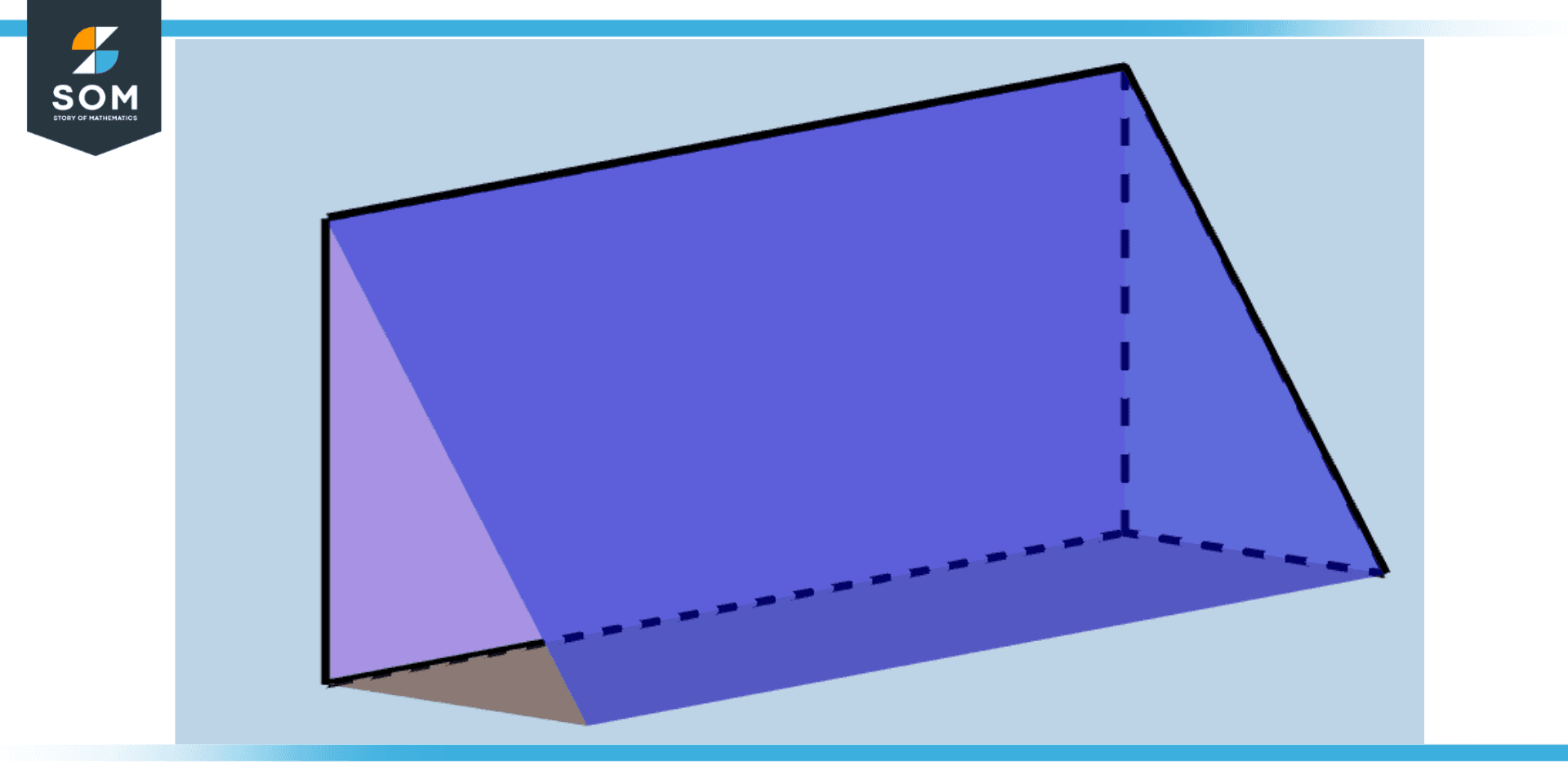
Figure 3 – Triangular Prism

This is a three-sided prism with two triangular bases and three rectangular faces. It is used to refract light at a specific angle or to disperse light into its various wavelengths.

Rectangular Prism

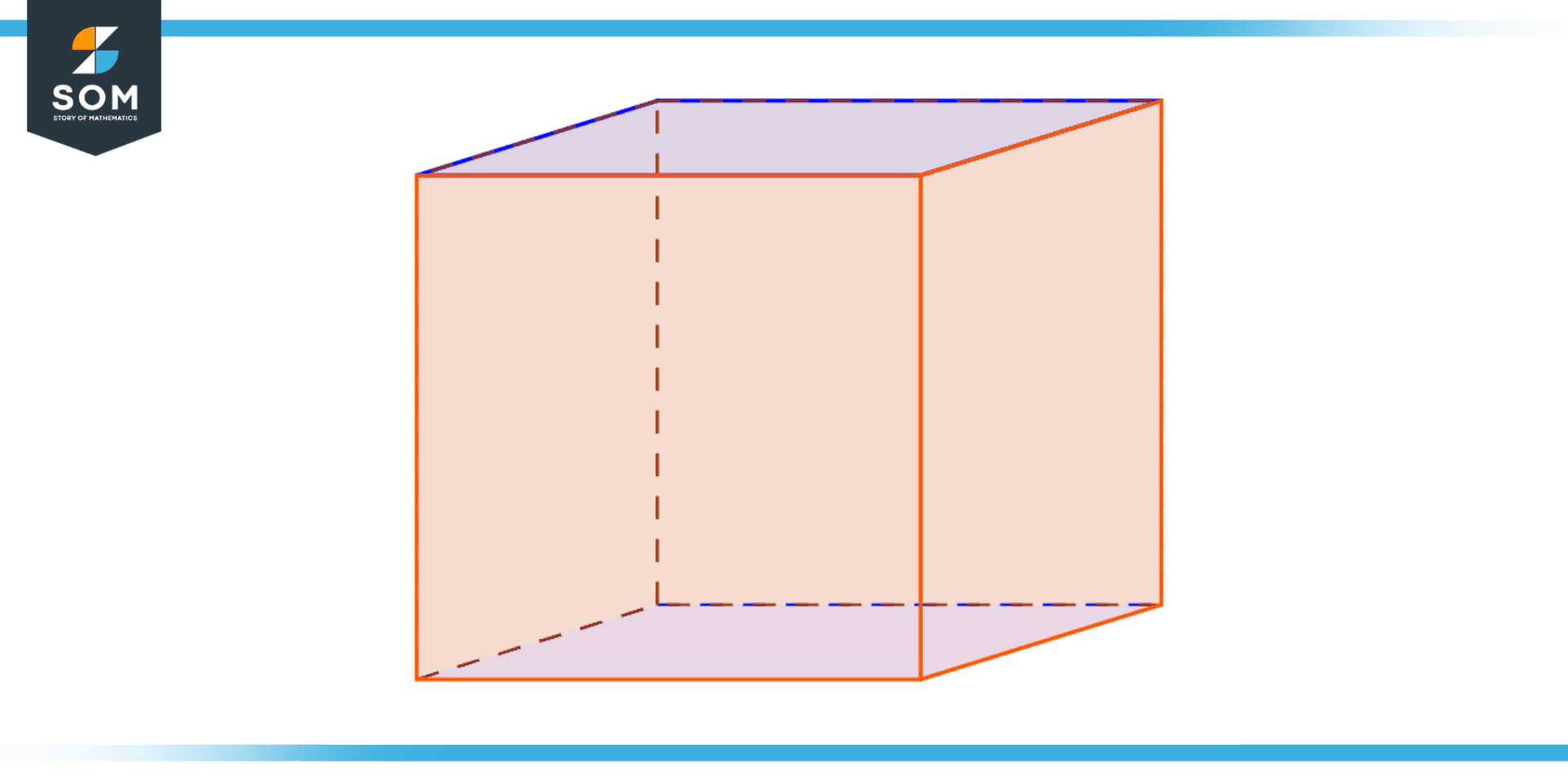
Figure 4 – Rectangular Prism

This is a six-sided prism with two rectangular bases and four rectangular faces. It is commonly used in optical instruments such as binoculars and telescopes.

Pentagonal Prism

This is a five-sided prism with two pentagonal bases and five rectangular faces. It is used in various applications, including laser systems and fiber optics.

Hexagonal Prism

This is a six-sided prism with two hexagonal bases and six rectangular faces. It is commonly used in optical instruments such as telescopes and microscopes.

Octagonal Prism

This is an eight-sided prism with two octagonal bases and eight rectangular faces. It is used in a variety of applications, including laser systems and fiber optics.

Conical Prism

This is a three-dimensional shape with a circular base and a pointed top. It is used to refract the light at a specific angle.

Spherical Prism

This is a three-dimensional shape with two spherical bases and curved faces. It is used to refract light in a variety of applications, including telescopes and microscopes.

Regular Vs. Irregular Prism

The main difference between regular and irregular prisms is the shape and size of their bases. A regular prism has bases that are congruent, or identical in shape and size, while an irregular prism has bases that are not congruent.

In addition to the difference in their bases, regular and irregular prisms may also differ in the following ways:

1. Sides: The sides of a regular prism are perpendicular to the bases and have equal angles between them, while the sides of an irregular prism may not be perpendicular to the bases and may have unequal angles between them.
2. Number of faces: A regular prism always has the same number of faces as it has edges. For example, a triangular prism has three faces and three edges, while a hexagonal prism has six faces and six edges. An irregular prism may have a different number of faces and edges.
3. Symmetry: Regular prisms have rotational symmetry, meaning they look the same when rotated about their axis. Irregular prisms may not have rotational symmetry.
4. Volume: The volume of a regular prism can be calculated using its base area and height. The volume of an irregular prism can be more difficult to calculate and may require more complex mathematical techniques.

Numerical Examples

Example 1

We are given the triangular prism whose base area is 50 cm² and whose height is 4cm. Calculate the volume of the prism.

Solution

Base Area = 50 cm²

Height = 4 cm

Volume = ?

We know that:

Volume = Base Area x Height

Volume = 50 cm² * 4 cm

Volume = 200 cm³

Example 2

We are given the prism whose base area is 30 cm² and the volume of the prism 120 cm³. Calculate the height of the prism.

Solution

Base Area = 30 cm²

Volume = 120 cm³

Height = ?

We know that:

Volume = base area x height

Height = $\dfrac{\text{Volume}}{\text{Base Area}}$

Height = $\dfrac{120 \text{ cm}^{3}}{30 \text{ cm}^{2}}$

Height = 4 cm

All mathematical drawings and images were created with GeoGebra.

Primitive Function Definition < Glossary Index > Problem Definition